- Geometrische Vielfachheit
-
Eigenraum ist ein Begriff aus der linearen Algebra. Er bezeichnet den von den Eigenvektoren zu einem bestimmten Eigenwert eines Endomorphismus aufgespannten Untervektorraum.
Inhaltsverzeichnis
Definition
Sei V ein Vektorraum über einem Körper K und
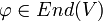 ein Endomorphismus. E(λ) heißt dann der Eigenraum zum Eigenwert λ von
ein Endomorphismus. E(λ) heißt dann der Eigenraum zum Eigenwert λ von  .
.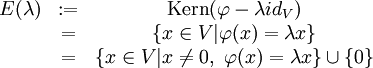
Man sagt dann auch,
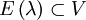 ist invariant bezüglich des Endomorphismus
ist invariant bezüglich des Endomorphismus  oder
oder 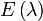 ist ein
ist ein  -invarianter Untervektorraum von V. Die Elemente x von
-invarianter Untervektorraum von V. Die Elemente x von 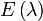 sind dann die Eigenvektoren zum Eigenwert λ von
sind dann die Eigenvektoren zum Eigenwert λ von  .
.Geometrische Vielfachheit
Die Dimension des Eigenraums
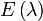 wird als geometrische Vielfachheit von λ bezeichnet. Sie ist dabei stets mindestens 1 und höchstens gleich der algebraischen Vielfachheit von λ.
wird als geometrische Vielfachheit von λ bezeichnet. Sie ist dabei stets mindestens 1 und höchstens gleich der algebraischen Vielfachheit von λ.Eigenschaften
- Existiert ein Eigenwert λ = 0 von
 , so ist der zugehörige Eigenraum
, so ist der zugehörige Eigenraum 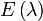 gleich dem Kern von
gleich dem Kern von  . Denn
. Denn 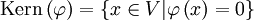 und nach Definition des Eigenraumes:
und nach Definition des Eigenraumes: 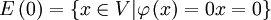 .
.
- Die Summe von Eigenräumen
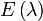 zu n verschiedenen Eigenwerten λ ist direkt:
zu n verschiedenen Eigenwerten λ ist direkt:
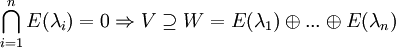
- Gilt im obigen Fall V = W, so besitzt V eine Basis aus Eigenvektoren. In diesem Fall ist die Matrix A von
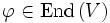 bezüglich einer Basis von V diagonalisierbar, das heißt die Matrix A' von
bezüglich einer Basis von V diagonalisierbar, das heißt die Matrix A' von  bezüglich der Basis von V aus Eigenvektoren hat Diagonalgestalt. In der Hauptdiagonalen von A' stehen dann die Eigenwerte von
bezüglich der Basis von V aus Eigenvektoren hat Diagonalgestalt. In der Hauptdiagonalen von A' stehen dann die Eigenwerte von  :
:
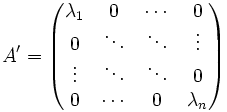
- Ist
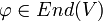 selbstadjungiert, so sind die Eigenräume zu verschiedenen Eigenwerten paarweise zueinander orthogonal.
selbstadjungiert, so sind die Eigenräume zu verschiedenen Eigenwerten paarweise zueinander orthogonal.
Siehe auch
Literatur
Gerd Fischer: Lineare Algebra, ISBN 3-528-03217-0
- Existiert ein Eigenwert λ = 0 von
Wikimedia Foundation.
