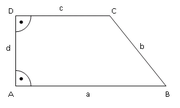
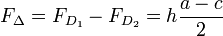Gleichschenkliges Trapez

Ein Trapez aus den Punkten ABCD mit der Höhe h und den Diagonalen e und f

Trapez

ist Spezialfall von

Viereck konvexes Viereck

umfasst als Spezialfälle

Parallelogramm Rhombus (Raute), Rechteck Quadrat

In der Geometrie ist ein Trapez (griech.: τράπεζα = Tisch) ein ebenes Viereck mit mindestens zwei parallel zueinander liegenden Seiten.

Allgemeines

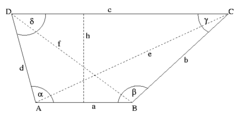
Die beiden parallelen Seiten werden Grundseiten des Trapezes genannt. Eine dieser Grundseiten (meistens die längere) wird oft als Basis des Trapezes bezeichnet, die beiden angrenzenden (im Allgemeinen nicht parallelen) Seiten als Schenkel. Im Trapez gibt es zwei Paare benachbarter Supplementwinkel (das heißt die Winkel ergänzen sich zu 180 Grad).

Die Höhe h des Trapezes ist der Abstand zwischen den zwei parallelen Seiten.

Jedes Trapez besitzt zwei Diagonalen, die einander im gleichen Verhältnis schneiden.

Ein Trapez ist entweder ein konvexes oder ein überschlagenes Viereck. Überschlagene Trapeze werden jedoch normalerweise nicht zu den (normalen oder "echten") Trapezen gerechnet.

Formeln zum Trapez
Flächeninhalt	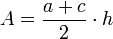$A = \frac{a+c}{2} \cdot h$
Umfang	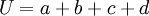$U = a + b + c + d\,$
Höhe	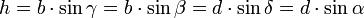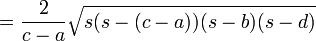$h = b \cdot \sin\gamma = b \cdot \sin\beta = d \cdot \sin\delta = d \cdot \sin\alpha$ $= \frac{2}{c-a} \sqrt{s (s-(c-a)) (s-b) (s-d)}$ (für a < c), mit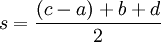 $s=\frac{(c-a)+b+d}{2}$
Abstand des Schwerpunkts von der Seite c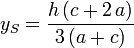	$y_S = \frac{h\,(c+2\,a)}{3\,(a+c)}$
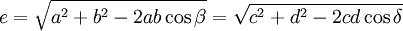
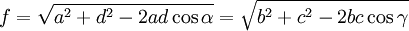
Diagonalenlänge	$e = \sqrt{a^2 + b^2 - 2ab\cos \beta} = \sqrt{c^2 + d^2 - 2cd\cos \delta}$ $f = \sqrt{a^2 + d^2 - 2ad\cos\alpha} = \sqrt{b^2 + c^2 - 2bc\cos\gamma}$
Seitenlängen	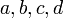$a,b,c,d\,$
Größen der Innenwinkel	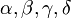$\alpha,\beta,\gamma,\delta\,$

Die Formel zur Berechnung der Höhe aus den Seitenlängen lässt sich aus der heronischen Formel für die Dreiecksfläche herleiten. Die Beziehungen für die Diagonalenlängen beruhen auf dem Kosinussatz.

Gleichschenklige und symmetrische Trapeze

Gleichschenkliges Trapez mit Umkreis

Ein Trapez heißt gleichschenklig, wenn die beiden Schenkel gleich lang sind. Somit ist ein gleichschenkliges Trapez entweder ein Parallelogramm, oder es ist ein symmetrisches Trapez, bei dem die zwei Innenwinkel an einer der parallelen Seiten gleich sind. Daraus folgt, dass auch die Innenwinkel an der anderen der parallelen Seiten gleich groß sind.

Die beiden Diagonalen sind im symmetrischen Trapez gleich lang.

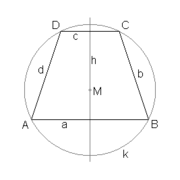
Die Eckpunkte eines symmetrischen Trapezes liegen auf einem Kreis k, dem Umkreis des Trapezes. Das Trapez ist somit ein Sehnenviereck dieses Kreises. Der Umkreismittelpunkt ist der Schnittpunkt der Mittelsenkrechten der Seiten des Trapezes. Das Trapez wird von der Höhe h, die durch den Umkreismittelpunkt M geht, in zwei spiegelsymmetrische Teile zerlegt (daher der Name).

Verschränktes Trapez

Verschränktes Trapez

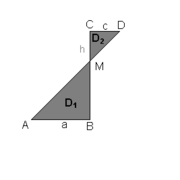
Ein verschränktes Trapez besteht aus zwei rechtwinkligen Dreiecken, die sich an einer Ecke berühren. Solch ein verschränktes Trapez kann man sich aus einem gewöhnlichen Trapez entstanden vorstellen: Ausgehend von einem gewöhnlichen Trapez wird eine der parallelen Seiten (z.B. c) so „umgedreht und verschoben“, dass B der Fußpunkt des Lotes von C auf a ist und D rechts statt links von C liegt. Somit ist ein verschränktes Trapez ein rechtwinkliges und überschlagenes (siehe Viereck) Trapez.

Verschränkte Trapeze werden in der Geodäsie zur Berechnung von Flächeninhalten nach dem Orthogonalverfahren verwendet. Die Differenz der Flächen der beiden Dreiecke ergibt sich zu

$F_\Delta = F_{D_1} - F_{D_2} = h\frac{a - c}2$

mit $h = \overline{BC}$.

Rechtwinkliges Trapez

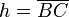Rechtwinkliges Trapez

Ein Trapez heißt rechtwinklig (oder auch orthogonal), wenn es mindestens einen rechten Innenwinkel besitzt. Damit besitzt ein rechtwinkliges Trapez immer mindestens zwei rechte Winkel, die nebeneinander liegen. Ein Rechteck ist somit immer auch ein rechtwinkliges Trapez.

Konvexe Vierecke

Quadrat | Rechteck | Raute | Parallelogramm | Drachenviereck | Trapez | Sehnenviereck | Tangentenviereck