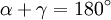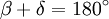Satz von Ptolemäus

Ein Sehnenviereck ABCD mit Umkreis k

Ein Sehnenviereck ist ein Viereck, dessen Eckpunkte auf einem Kreis liegen, dem Umkreis des Vierecks. Folglich sind alle Seiten des Sehnenvierecks Sehnen des Umkreises. Üblicherweise meint man mit Sehnenviereck ein nicht überschlagenes Sehnenviereck, dieses ist notwendigerweise konvex.

Sätze über Sehnenvierecke (Auswahl)

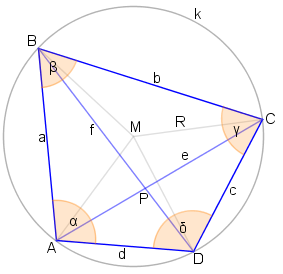
Das Sehnenviereck wird mit ABCD bezeichnet.

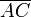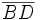1. Die Produkte je zweier gegenüberliegender Diagonalenabschnitte sind gleich groß. Das heißt, wenn P der Schnittpunkt von $\overline{AC}$ und $\overline{BD}$ (Diagonalenschnittpunkt) ist, so gilt $\overline{AP}\cdot\overline{CP}=\overline{BP}\cdot\overline{DP}$.

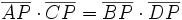Die folgenden Sätze gelten nur für nicht überschlagene Sehnenvierecke ABCD:

1. Gegenüberliegende Winkel ergänzen sich zu 180°, also α + γ = β + δ = 180° (Nachweis weiter unten).
2. Satz von Ptolemäus: Die Summe der Produkte gegenüberliegender Seiten des Sehnenvierecks ist gleich dem Produkt der Diagonalen: $\overline{AB}\cdot\overline{CD}+\overline{BC}\cdot\overline{DA}=\overline{AC}\cdot\overline{BD}$.

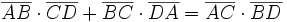Formeln zum Sehnenviereck
Flächeninhalt	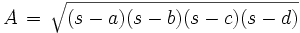$A \, = \, \sqrt{(s-a) (s-b) (s-c) (s-d)}$
Flächeninhalt	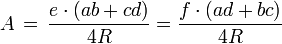$A \, = \, \frac{e \cdot (ab+cd)}{4R} = \frac{f \cdot (ad+bc)}{4R}$
Seitenlängen	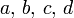$a,\,b,\,c,\,d$
Halber Umfang	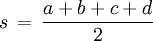$s \, = \, \frac{a+b+c+d}{2}$
Diagonalenlängen	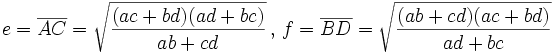$e = \overline{AC}=\sqrt{\frac{(ac+bd)(ad+bc)}{ab+cd}}\, , \, f=\overline{BD}=\sqrt{\frac{(ab+cd)(ac+bd)}{ad+bc}}$
Umkreisradius	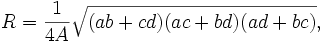$R=\frac{1}{4A}\sqrt{(ab+cd)(ac+bd)(ad+bc)},$

Die zuerst genannte Flächenformel ist verwandt mit der Heron'schen Flächenformel für Dreiecke und wird als Formel von Brahmagupta bezeichnet.

Gegenüberliegende Winkel im Sehnenviereck

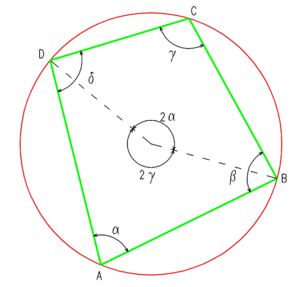
Im Sehnenviereck beträgt die Winkelsumme der gegenüberliegenden Winkel 180°.

$\, \alpha + \gamma = 180^\circ$

$\, \beta + \delta = 180^\circ$

Der Beweis ergibt sich unmittelbar aus dem Kreiswinkelsatz, da zwei gegenüberliegende Winkel des Sehnenvierecks Umfangswinkel über zwei komplementären Kreisbögen sind, deren Mittelpunktswinkel sich zu 360° ergänzen. Da Umfangswinkel halb so groß sind wie Mittelpunktswinkel über dem gleichen Bogen, müssen sich die Umfangswinkel zu 360°/2 = 180° ergänzen.

Ein anderer Beweis findet sich im Beweisarchiv.

Verwandte Vierecke

Ein Sehnenviereck, das gleichzeitig Trapez ist, heißt gleichschenkliges Trapez. Jedes Rechteck ist ein gleichschenkliges Trapez und damit ein Sehnenviereck.

Ein Viereck, das einen Inkreis hat, heißt Tangentenviereck.

Siehe auch

Japanischer Satz für konzyklische Vierecke

Weblinks

• Beweis des Satzes von Ptolemäus (mit Umkehrung) mit geometrischen Mitteln der gymnasialen Mittelstufe, Landesbildungsserver Baden-Württemberg

Konvexe Vierecke

Quadrat | Rechteck | Raute | Parallelogramm | Drachenviereck | Trapez | Sehnenviereck | Tangentenviereck