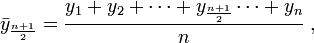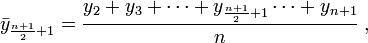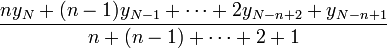Gleitendes Mittel

Der gleitende Mittelwert wird auch gleitender Durchschnitt genannt. Gleitende Mittelwerte verringern die in einer Datenreihe vorhandene Variation. Daher werden sie oft verwendet, um Zeitreihen zu glätten.

Einfacher gleitender Mittelwert

Bei einer gegebenen Menge von Zahlen (Datenpunkten), in der Regel Zeitreihen, y1, y2, ... definiert man einen gleitenden Mittelwert 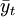$\bar y_t$ der Ordnung n als Folge der arithmetischen Mittelwerte aufeinanderfolgender Datenpunkte.

Für eine ungeradzahlige Ordnung ergibt sich die Reihe

$\bar y_{\frac{n+1}{2}}= {y_1 + y_2 + \cdots + y_{\frac{n+1}{2}} \cdots + y_n \over n } \; ,$

$\bar y_{\frac{n+1}{2}+1}= { y_2 + y_3 + \cdots + y_{\frac{n+1}{2}+1} \cdots + y_{n+1} \over n } \; ,$

$\cdots$

Der Zeitreihenwert in der Mitte der Zählersumme gibt den Index t für 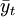$\bar y_t$ vor. Für die ersten und letzten 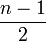$\frac{n-1}{2}$ Zeitreihenwerte liegt also kein gleitender Durchschnittswert vor.

Gewichteter gleitender Mittelwert

Ein gewichteter gleitender Mittelwert ordnet den Datenpunkten Gewichte zu. Bei einem gewichteten Mittelwert im engeren Sinn sind diese Gewichte arithmetisch abnehmende Werte.
Für den gewichteten gleitenden Mittelwert der Ordnung n erhält der jüngste Datenpunkt yN das Gewicht "n", der vorletzte "n-1", etc..

${ n y_N + (n-1) y_{N-1} + \cdots + 2 y_{N-n+2} + y_{N-n+1} \over n + (n-1) + \cdots + 2 + 1}$

Exponentiell geglätteter Mittelwert

Der exponentiell geglättete Mittelwert (exponentielle Glättung) ordnet Datenpunkten exponentiell abnehmende Gewichte zu. Somit werden jüngere Datenpunkte stärker gewichtet als weiter zurückliegende Datenpunkte.

Vergleich mit Digitalfilter

Die Berechnungsvorschrift stellt im Prinzip nichts anderes als ein digitales Tiefpassfilter dar. Der einfache gleitenden Mittelwert entspricht einem FIR-Filter mit N Gliedern, wobei alle Faktoren gleich sind. Beim gewichteten gleitenden Mittelwert sind die Faktoren zwar unterschiedlich, aber so gewählt, dass die Summe den Wert 1 ergibt. Der exponentiell geglättete Mittelwert entspricht einem IIR-Filter 1. Ordnung.

Siehe auch

• Exponentielle Glättung
• ARMA-Modell
• Mittelwert

Weblinks