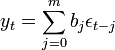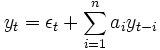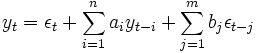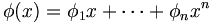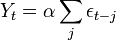ARMAX

Das Akronym ARMA (AutoRegressive-Moving Average) und die daran angelehnten Kunstwörter ARMAX und ARIMA bezeichnen lineare Modelle für stationäre, zeitdiskrete stochastische Prozesse. Sie werden zur Zeitreihenanalyse in der Messtechnik, in der Statistik und dort insbesondere in der Ökonometrie eingesetzt. Hier sind sie auch unter dem Namen Box-Jenkins-Modelle bekannt. Die Prognosemodelle der Wirtschaftsinstitute und Banken sind in der Regel aus ARMA-Modellen zusammengesetzt. Ihr mathematischer Kern ist ein lineares Gleichungssystem. Man kann solche Modelle auch als Differenzengleichungen bzw. Differenzengleichungssysteme ansehen.

Mathematische Definition eines ARMA-Prozesses

In das Modell fließen Rauschterme und gewichtete frühere Werte der Zeitreihe linear ein. ARMA-Modelle sind eines der Hauptwerkzeuge zur Vorhersage von beobachteten, stochastischen Signalen. Sind die zu modellierenden Signale nicht stationär, dann muss man sie gegebenenfalls vor der Modellierung differenzieren, um den Trend zu beseitigen.

MA-Modell

$y_t=\sum_{j=0}^m b_j \epsilon_{t-j}$

Das Signal setzt sich aus einem, durch gleitendes Mittel (Moving Average) der Länge m geglätteten Signal, einer (nicht direkt messbaren) anderen Zeitreihe und einem Rauschterm (j=0) zusammen.

Siehe auch: FIR-Filter

AR-Modell

$y_t=\epsilon_t + \sum_{i=1}^n a_i y_{t-i}$

Das Signal setzt sich aus einem geglätteten Signal seiner n vorhergehenden Werte und einem Rauschterm zusammen.

Siehe auch: IIR-Filter (Infinite Impulse Response-Filter)

ARMA-Modell

$y_t=\epsilon_t + \sum_{i=1}^n a_i y_{t-i} + \sum_{j=1}^m b_j \epsilon_{t-j}$

Dieses Modell wird auch als ARMA(n,m)-Modell bezeichnet, wobei n und m die Ordnung des Prozesses heißen.
Mit Hilfe des so genannten Verschiebungsoperators L (von lag=Zeitverschiebung):

L^dx_t = x_{t − d}

schreibt man kürzer auch:

(1 + φ(L))y_t = (1 + θ(L))ε_t

wobei φ und θ beides endliche Polynome (der Grade n und m) darstellen:

$\phi(x) = \phi_1 x+ \cdots + \phi_n x^n$

Inhaltliche Interpretation: Was ist MA und was ist AR?

Moving Average

ε_t ist ein so genanntes weißes Rauschen, eine Zufallsvariable, die für alle t paarweise unabhängig und gleich verteilt ist mit Erwartungswert μ und der Varianz σ². Die Abhängigkeit beschränkt sich bei MA-Termen auf den Erwartungswert: Ist

$Y_t=\alpha \sum_{j}^{} \epsilon_{t-j}$

dann wird lediglich der Erwartungswert von Y mit jedem Zeitschritt um αμ verschoben. Y_t selbst ist stochastisch bestimmt.

Auto-Regression

Anders beim Auto-Regressionsteil: Hier ist Y_t deterministisch von der Vergangenheit abhängig. In

Y_t = Y_{t − 1} + ε

unterliegt Y_t genau dann einer Störung, wenn Y_{t − 1} einer Störung unterliegt.

ARMA-Modelle in der Statistik

Regressionsmodelle spielen in der Statistik eine große Rolle. In der Ökonometrie müssen oft mehrere Zeitreihen der Form x₁(t),x₂(t)...x_n(t) miteinander in Zusammenhang gebracht werden, die s.g. Wirtschaftsindikatoren, also z.B. Zins, Arbeitslosigkeit, Investitionen usw. Man unterscheidet zwischen endogenen zeitabhängigen Variablen Y(t) (die also vom Modell erklärt werden) und exogenen Variablen X(t), die von außen definiert werden. Mit ihnen kann man das allgemeine lineare Gleichungssystem

BY = AX + ε

formulieren. B, Y, A und X sind Matrizen mit sovielen Zeilen wie Beobachtungen und sovielen Spalten wie Variablen des jeweiligen Typs. Jeder Zeitpunkt zählt als Beobachtung. Geht einunddieselbe Variable zu verschiedenen Zeitpunkten (also als Y(t), Y(t-1) usw.) in das Gleichungssystem ein, so zählt dies als mehrere Variablen. Die Gleichung Y(t) = β₁Y(t − 1) + β₂Y(t − 2) + ε hat also drei Variablen. Das ist entscheidend für die ARMA-Modelle. ε ist ein Vektor mit sovielen Zeilen wie Beobachtungen.

ARMAX und ARIMA

Ist der Regressor X dabei, spricht man von ARMAX-Modellen. Gehen nur die Differenzen von Y in das Modell ein, so dass hinterher die Modellprognosen wieder “integriert” werden müssen, so spricht man von ARIMA-Modellen, das I steht für "Integrated". Die Differenzen sollen hierbei für die Berechnung ein stationäres und um nicht-saisonale Trends bereinigtes Modell erzeugen.

Alle Modelle der ARMA-Familie haben dieses lineare Gleichungssystem zur Grundlage. Viele Systeme können mit einer einfachen linearen Regression geschätzt werden. Voraussetzung, dass die Standardfehler der Schätzer unverzerrt sind, ist, dass die Störterme ε von Y nicht autokorrelieren, da Korrelation der Fehler untereinander zwar nicht den Schätzer selbst, jedoch den zugehörigen Standardfehler verzerrt (meist wird er stark unterschätzt). Wenn Autoregressionsterme der Form

$y_t=\epsilon_t + \sum_{i=1}^n a_i y_{t-i}$

vorliegen, liegt in der Regel eine solche Autokorrelation der Störterme vor.

Interpretation des Moving Average-Teils

Das LGS wird um einen Term der Form

$\epsilon=\sum_{j=1}^m \gamma_j \epsilon_{t-j}+\epsilon'$,

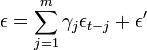also um eine Autoregression der Fehlerterme erweitert. Praktisch spielen vor allem Erweiterungen der Ordnung 1:

ε = γ₁ε_{t − 1} + ε'

eine Rolle. Das ist ein Markow-Prozess.

Der Begriff "MA" für solche rein stochastischen Prozesse ist eher irreführend. ARMA-Modelle sind also Simultan-Modelle für deterministische Zusammenhangsmodelle (AR-Anteil, entspricht Regressionsmodell) und stochastischen Prozessen (MA-Anteil).

ARMA-Modelle (auch ARMAX, ARIMA) werden durch nichtlineare Regressionsverfahren geschätzt.

Siehe auch

Autokorrelation, Digitales Filter, X-12-ARIMA

Literatur

• Box, G.E.P. and Jenkins, G.M. (1970) Time series analysis: Forecasting and control, San Francisco: Holden-Day
• McCleary, R. and Hay, R.A. (1986) Applied Time Series Analysis for the Social Sciences, Beverly Hills: Sage Publications
• Hamilton, James D. (1994) Time Series Analysis, Princeton: Princeton University Press
• Enders, W. (1995) Applied Econometic Time Series, John Wiley & Sons INC.
• Mills, Terence C. (1999) The Econometric Modelling of Financial Time Series, 2nd Edition, Cambridge University Press
• Tsay, Ruey S. (2005) Analysis of Financial Time Series, 2nd Edition, Wiley Series in Prob. and Statistics
• Stier, W. (2001) Methoden der Zeitreihenanalyse, Springer