Gluschkow-Verfahren

Beim Berry-Sethi Verfahren (nach Gérard Berry und Ravi Sethi; auch Glushkov-Konstruktion, nach Viktor Glushkov) handelt es sich um einen Algorithmus zur Überführung eines regulären Ausdrucks in einen nichtdeterministischen endlichen Automaten.

Zunächst wird dabei der reguläre Ausdruck in eine Baumstruktur überführt. Die Knoten entsprechen den Regeln des regulären Ausdrucks (z.B. * oder |). Die Blätter repräsentieren die Elemente des Eingabealphabets, also genau die Zeichen aus denen sich gültige Wörter zusammensetzen können. Alle weiteren Berechnungen finden mithilfe dieser Darstellungsform statt.

Stellt man sich nun einen Punkt vor, der beginnend bei der Wurzel des Syntaxbaums um den Baum herumwandert, so können sukzessive alle Wörter des regulären Ausdrucks erzeugt werden. Mit Hilfe dieses Punktes wird nun der endliche Automat konstruiert. Die Zeitkomplexität des Verfahrens ist $\mathcal O (n^3)$

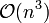
Vorgehensweise

1. Bestimme empty[r] für alle Knoten r des Baumes. Dies ist mit einer post-order DFS möglich (DFS: Depth-First Search, Tiefensuche).
2. Bestimme first[r] für alle Knoten r des Baumes. Dies ist mit einer post-order DFS möglich.
3. Bestimme next[r] für alle Knoten r des Baumes. Dies ist mit einer pre-order DFS möglich.
4. Bestimme last[r] für alle Knoten r des Baumes. Dies ist mit einer post-order DFS möglich.
5. Integration:
   1. Die Zustände des Automaten sind: $\{ \bullet e \} \cup \{i \bullet \mid \mbox{i ist Blatt}\}$
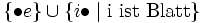
   2. Der Startzustand des Automaten ist: $\bullet e$
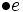
   3. Der Endzustand des Automaten ist:
      1. last[e], falls empty[e] = false und
      2. $\{\bullet e\} \cup last[e]$, falls empty[e] = true
   4. Die Übergänge des Automaten sind:
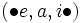      1. $( \bullet e, a, i\bullet)$, falls $i \in first[e]$ und i mit a beschriftet ist, und
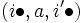      2. $( i \bullet, a, i'\bullet)$, falls $i' \in next[i]$ und i' mit a beschriftet ist.

Das Symbol $\bullet$ markiert hierbei den Punkt, der um den Baum herumwandert. Der resultierende endliche Automat ist im allgemeinen nichtdeterministisch und kann daher noch durch die Potenzmengenkonstruktion deterministisch gemacht werden.

Literatur

• Gérard Berry und Ravi Sethi: From regular expressions to deterministic automata. Theoretical Computer Science 48 (1986) 117–126.
• Viktor M. Glushkov: The abstract theory of automata. Russian Mathematical Surveys 16 (1961) 1-53.