- Greedy-Algorithmen
-
Greedy-Algorithmen bzw. Gierige Algorithmen bilden eine spezielle Klasse von Algorithmen, wie sie in der Informatik auftreten. Sie zeichnen sich dadurch aus, dass sie schrittweise denjenigen Folgezustand auswählen, der zum Zeitpunkt der Wahl den größten Gewinn bzw. das beste Ergebnis verspricht (z. B. Gradientenverfahren). Um unter den Folgezuständen eine Auswahl zu treffen, wird oft eine Bewertungsfunktion verwendet.
Greedy-Algorithmen sind meist schnell, lösen viele Probleme aber nicht optimal.
Inhaltsverzeichnis
Optimierungsprobleme auf Unabhängigkeitssystemen
Ein Greedy-Algorithmus findet für ein Optimierungsproblem auf Unabhängigkeitssystemen die optimale Lösung, wenn die zulässigen Lösungen die unabhängigen Mengen eines Matroids sind. Sonst führt der Algorithmus lediglich zu einem lokalen Optimum. Beispiele dafür sind das Rucksackproblem und das Problem des Handlungsreisenden. Bei diesen Problemen ist es wesentlich aufwändiger, die optimale Lösung zu finden, da die Probleme NP-vollständig sind.
Algorithmus für das Maximierungsproblem
Zu einem Matroid (E,U) sei eine Gewichtsfunktion
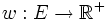 gegeben. Der folgende Algorithmus findet eine schwerste unabhängige Menge, bestimmt also ein
gegeben. Der folgende Algorithmus findet eine schwerste unabhängige Menge, bestimmt also ein 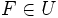 , das
, das 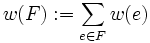 maximiert:
maximiert:01 // Ordne alle Elemente in E nach absteigendem Gewicht 02 03
04
03
04 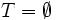 ;
05
06 for (k = 1; k <= n; k++) {
07 if
;
05
06 for (k = 1; k <= n; k++) {
07 if 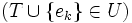 08
08  09 }
10
11 Ausgabe der Lösung T
09 }
10
11 Ausgabe der Lösung T
Verallgemeinerbarkeit
Der Algorithmus löst auch Maximierungs- und Minimierungsprobleme zu beliebigen Gewichtsfunktionen
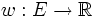 : In einer Lösung für das Maximierungsproblem treten negative Gewichte nicht auf, Elemente mit negativem Gewicht können also vom Algorithmus ignoriert werden. Die Lösung des Problems, eine minimale unabhängige Menge zu finden, können wir auf die Lösung des Maximierungsproblems zurückführen, indem wir die Gewichte durch ihre additiven Inversen ersetzen.
: In einer Lösung für das Maximierungsproblem treten negative Gewichte nicht auf, Elemente mit negativem Gewicht können also vom Algorithmus ignoriert werden. Die Lösung des Problems, eine minimale unabhängige Menge zu finden, können wir auf die Lösung des Maximierungsproblems zurückführen, indem wir die Gewichte durch ihre additiven Inversen ersetzen.Laufzeit
Ist L die Laufzeit der Prüfung einer Menge auf Unabhängigkeit, so ist die Laufzeit des Algorithmus durch O( | E | (log( | E | ) + L)) gegeben. Im besten Fall wird sie also durch das Sortierverfahren dominiert. Wenn die Unabhängigkeitsprüfung dagegen NP-vollständig ist, ist der Algorithmus praktisch nutzlos.
Beispiele
- Algorithmus von Kruskal für die Suche nach einem minimalen Spannbaum
- Algorithmus von Prim für die Suche nach einem minimalen Spannbaum (das zugrundeliegende Mengensystem – die Menge der Bäume – ist aber kein Unabhängigkeitssystem)
- Algorithmus von Dijkstra zur Suche eines kürzesten Weges
Algorithmus für das Minimierungsproblem
Zu einem Matroid (E,U) sei eine Gewichtsfunktion
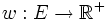 gegeben. Der folgende Algorithmus findet eine leichteste Basis, bestimmt also unter den kardinalitätsmaximalen
gegeben. Der folgende Algorithmus findet eine leichteste Basis, bestimmt also unter den kardinalitätsmaximalen 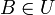 eines, das
eines, das 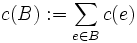 minimiert:
minimiert:- Sortiere E, so dass
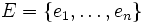 mit
mit 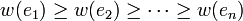
- T := E
- Für jedes i von 1 bis n:
-
- Enthält
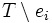 eine Basis, so setze
eine Basis, so setze 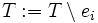 .
.
- Enthält
- Gib T aus.
Vergleich zum Maximierungsproblem, Verallgemeinerbarkeit
Da wir positive Gewichte vergeben, ist das Problem, nach einer leichtesten Basis-Obermenge zu suchen, äquivalent. Dieses Problem ist dual zum Maximierungsproblem und kann analog auf beliebige Gewichtsfunktionen und das entsprechende Minimierungsproblem verallgemeinert werden.
Laufzeit
Ist L die Laufzeit der Prüfung, ob eine Teilmenge von E Obermenge einer Basis ist, so ist die Laufzeit des Algorithmus durch O( | E | (log( | E | ) + L)) gegeben. Im besten Fall wird sie also durch das Sortierverfahren dominiert. Wenn die Basis-Obermengen-Prüfung dagegen NP-vollständig ist, ist der Algorithmus praktisch nutzlos.
Literatur
- Thomas H. Cormen, Charles Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, 2001, ISBN 0-262-53196-8
- Bernhard Korte, Jens Vygen: Combinatorial Optimization. 3. Auflage. Springer, 2005, ISBN 3-540-25684-9
Wikimedia Foundation.
