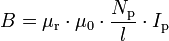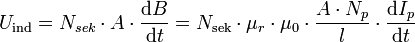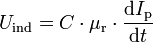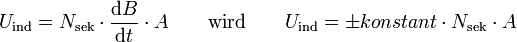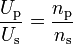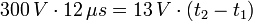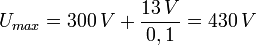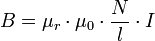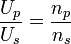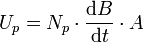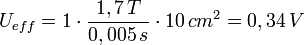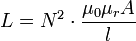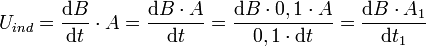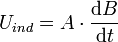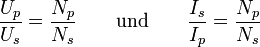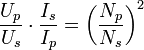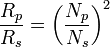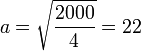Grundlagen des Transformators

Ein Transformator kann primärseitig mit Wechselspannung beliebiger Kurvenform und – bei geeigneter Dimensionierung in Schaltreglern – kurzzeitig sogar Gleichspannung betrieben werden. Sekundärseitig können erhebliche Abweichungen der Kurvenform auftreten. Nachfolgend werden die Begründungen und Bemessungsgrundlagen für hohe und tiefe Frequenzen dargestellt.

Abwärtstransformator mit physikalischen Symbolen

Symmetriertrafo, Impedanzwandler in einer Antennenleitung 60 Ω / 240 Ω für den Frequenzbereich 50…250 MHz mit Ferrit-Doppellochkern

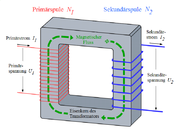
Primär- und Sekundärwicklung

Prinzip eines zweischenkligen Trafos

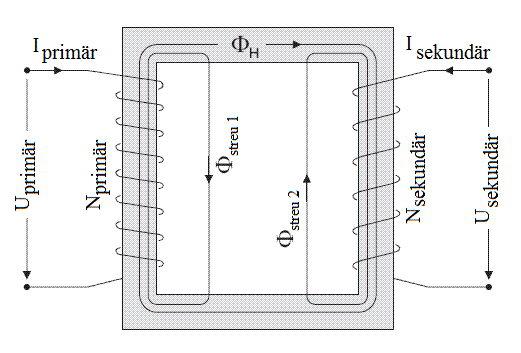
Die Primärwicklung eines Trafos mit N_primär Windungen und der Länge l wird vom Primärstrom I_primär durchflossen, wodurch ein Magnetfeld erzeugt wird, das im Inneren der Spule besonders stark ist. Die magnetische Flussdichte beträgt dort:

$B= \mu_\mathrm{r} \cdot \mu_0 \cdot \frac{N_\mathrm{p}}{l} \cdot I_\mathrm{p}$

Dabei ist μ₀ die Magnetische Feldkonstante und μ_r die Permeabilitätszahl des Spulenkerns. Wenn sich dieses Magnetfeld nicht ändert, wird auch keine Spannung induziert. Wenn es sich ändert, wird in einer oder mehreren Sekundärspule(n) ebenso wie in der Primärspule (Selbstinduktion) eine Wechselspannung induziert, die proportional zur Windungszahl steigt. Die Kurvenform der Sekundärspannung kann von der Kurvenform der Primärspannung erheblich abweichen.

Es gibt unterschiedliche Möglichkeiten, elektrische Spannung durch Elektromagnetische Induktion zu erzeugen. Der für den Trafo relevante Teil der etwas umfangreichen Gleichung lautet

$U_\mathrm{ind}=N_{sek}\cdot A\cdot \frac{\mathrm{d}B}{\mathrm{d}t} =N_\mathrm{sek}\cdot \mu_r \cdot \mu_0 \cdot \frac{A\cdot N_p}{l}\cdot \frac{\mathrm{d}I_p}{\mathrm{d}t}$

wenn man, wie üblich, die N_sek Windungen der Sekundärspule eng anliegend auf den Eisenkern mit der Querschnittsfläche A wickelt. Fasst man alle uninteressanten und konstanten Faktoren in C zusammen, erhält man

$U_\mathrm{ind}=C\cdot \mu_\mathrm{r} \cdot \frac{\mathrm{d}I_\mathrm{p}}{\mathrm{d}t}$

In dieser Gleichung ist klar ersichtlich, dass es für den Betrag der induzierten Spannung nur darauf ankommt, wie schnell sich I_p ändert und wie sich μ_r verhält.

• Der Quotient dI_p/dt (die zeitliche Änderung) muss groß sein, denn die Zeitdifferenz dt steht im Nenner. Das hat eine weitreichende Auswirkung: Je kleiner dt ist, also je schneller sich der Strom ändert, desto größer ist die induzierte Spannung. Das wird in Impulstrafos wie Zündspule und Funkeninduktor oder beim Elektrozaun ausgenutzt, um durch schnelles Abschalten des Stromes Hochspannung zu erzeugen. Bei Betrieb mit Gleichstrom lässt sich diese Hochspannung mit einer parallel geschalteten Freilaufdiode verhindern, wenn sie nicht gewünscht ist. Zum Beispiel beim Ausschalten von Schützspulen. Der Stromverlauf beim Einschalten einer Spule mit einer Gleichspannung wird hier erklärt.
• Der Materialparameter μ_r hat in Luft den Wert 1. Das ist problemlos, sorgt aber bei langsamen Stromänderungen für geringe induzierte Spannung.
• Falls (bei tiefen Frequenzen) die Primärspule einen Eisenkern besitzt, ist μ_r viel größer, aber leider nicht konstant und kann zwischen etwa 50.000 und 1 schwanken. Das ist Ursache für eine Reihe von Problemen, die bei luftgefüllten Trafos nicht existieren.

Drei häufige Formen von Wechselspannung

Beispiel: Das Magnetfeld ändere sich in 2 ms um 0,3 T, dann ist dB/dt = 150 T/s. Mit einer richtig orientierten Spulenfläche von 6 cm² erhält man 90 mV pro Windung.

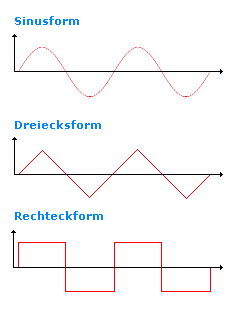
Ein Trafo kann die Kurvenform und/oder die Phase von Wechselstrom ändern. Um dieses Übertragungsverhalten zu verstehen, kann man die Primärspule an einen Funktionsgenerator legen und Kurvenformen wie Dreieckspannung, Rechteckspannung oder sinusförmigen Wechselspannung wählen.

Betrieb mit einer Dreiecksspannung

Das Übertragungsverhalten eines Trafos lässt sich auch erklären, wenn man statt der üblichen sinusförmigen Wechselspannung des Stromnetzes eine Dreieckspannung aus einem Funktionsgenerator anlegt, weil dann die physikalischen Gleichungen leichter zu durchschauen sind. Dabei sind zwei Fälle zu unterscheiden: Bei der verwendeten Frequenz ist der induktive Widerstand der Primärspule

• viel kleiner als ihr ohmscher Widerstand; dann ist die Phasenverschiebung zwischen Strom und Spannung fast Null und es gelten die Proportionalitäten: U_primär ≈ I_primär ≈ B ≈ Φ;
• viel größer als der ohmsche Widerstand. Dann besteht zwischen Strom und Spannung eine Phasenverschiebung.

Betrieb mit eingeprägtem Strom

Der Trafo differenziert:
Input = Dreieckstrom,
Output = Rechteckspannung

Der Trafo differenziert:
Input = abgeschnittener Dreieckstrom,
Output = Rechteckspannung mit 0-Volt-Linien

Transformator mit eingeprägtem Strom: primär Dreieckspannung vor dem Vorwiderstand, sekundär Rechteckspannung

Die Primärspule wird mit eingeprägtem Strom betrieben, wenn die Dreieckspannung über einen ausreichend großen Vorwiderstand eingespeist wird, der mindestens zehnmal größer ist als die Impedanz der Primärspule. Der Vorwiderstand kann auch der ohmsche Widerstand der Spule sein. Diese Bedingung wird von jedem Trafo erfüllt, wenn die Frequenz nur ausreichend tief ist, weil der induktive Widerstand proportional zur Betriebsfrequenz sinkt.

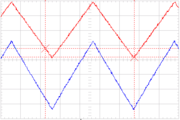
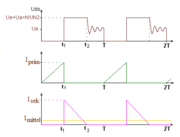
Hier sind Spannung U_primär und Strom I_primär aus steigenden und fallenden Geradenstücken zusammengesetzt (blaue Dreiecksfunktion im Bild links). Weil die Ableitung einer Geraden konstanten Wert besitzt, gilt in Verbindung mit der Proportion U_primär ≈ I_primär ≈ B ≈ Φ die einfache Aussage dΦ/dt = ±konstant und aus der Gleichung

$U_\mathrm{ind}=N_\mathrm{sek}\cdot \frac{\mathrm{d}B}{\mathrm{d}t}\cdot A\qquad \text{wird}\qquad U_\mathrm{ind}=\pm konstant\cdot N_\mathrm{sek}\cdot A$

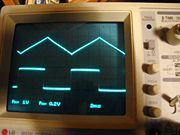
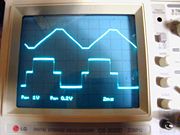
Die sekundärseitig induzierte Spannung kann also nur zwischen zwei Werten wechseln. Sie ist genau so lange konstant, wie die Primärspannung steigt und ändert ihr Vorzeichen, wenn die Primärspannung fällt, wie im nebenstehenden Bild rot eingezeichnet ist. Die Übergänge erfolgen schlagartig. Mathematisch gesehen, differenziert diese Anordnung die angebotene Dreieckspannung bzw. den Strom (beide sind über U = R·I verknüpft). Wenn die Dreieckspannung schneller steigen als fallen würde (asymmetrische Kippschwingung), wäre während der Steigzeit auch U_sek deutlich größer.

Beim Vergleich der beiden Oszillogramme erkennt man, was ein stückweise konstanter Primärstrom bewirkt: Sobald sich I_primär nicht ändert, weil die Spitzen der Dreiecke abgeschnitten werden, kann der Eisenkern zwar magnetisiert sein, das B-Feld ändert sich aber nicht und deshalb wird in der Sekundärspule keine Spannung induziert. Während der Zeitspannen, in denen die Dreieckspannung flache Stellen hat, zeigt das Oszillogramm null Volt an.

Falls der Trafo einen Eisenkern besitzt, kann dieser bei großen Strömen magnetisch gesättigt werden. Dann sinkt μ_r von sehr hohen Werten um 5000 auf nur 1. Aus der obigen Gleichung folgt dann, dass die Flussdichte B kaum noch zunehmen kann (dB wird Null), auch wenn der Primärstrom stark ansteigt. Das hat die gleiche Konsequenz wie ein konstanter Strom: Die induzierte Sekundärspannung wird Null.

Die Eigenschaft, dass jeder Transformator I_primär differenziert, bewirkt beim Stromwandler und bei der Rogowskispule, dass Gleichströme nicht gemessen werden können.

Betrieb mit eingeprägter Spannung

Transformator mit eingeprägter Dreieckspannung, sekundär ebenfalls Dreieckspannung

Die Primärspule wird mit eingeprägter Spannung betrieben, wenn die Impedanz der Spule mindestens zehnmal größer ist als ihr ohmscher Widerstand. Das kann bei jedem Trafo durch ausreichend hohe Frequenz erreicht werden. Bei tiefen Frequenzen (Netzfrequenz) wählt man meist einen zusätzlichen Eisenkern mit großem μ_r, um die Induktivität zu vergrößern. U_primär wird dann mit unveränderter Kurvenform übertragen, solange der Kern nicht in Sättigung gerät. Die Begründung:

• Die angelegte Wechselspannung U_primär lässt in der Primärspule einen Wechselstrom fließen, der im Eisenkern ein magnetisches Wechselfeld erzeugt.
• Dieses induziert in allen Spulen des Trafos, also auch in der Primärspule eine „Gegenspannung“ U_induziert, die fast so groß ist wie die angelegte Wechselspannung und diese weitgehend kompensiert (Lenzsche Regel). Als „Antriebsspannung“ für den Primärstrom steht nur die geringe Differenzspannung U_primär - U_induziert zur Verfügung, die am ohmschen Widerstand des Spulendrahtes abfällt. Deshalb ist der Primärstrom so gering.
• Wäre die Gegenspannung zu gering, würde die Differenzspannung U_primär - U_induziert sofort größer werden und höheren Primärstrom fließen lassen. Dadurch würde aber das Magnetfeld ansteigen und mehr Gegenspannung erzeugen. Dieses Verhalten nennt man dynamisches stabiles Gleichgewicht. Es sorgt in jedem Moment dafür, dass die induzierte Spannung „parallel“ zur angelegten Wechselspannung mitläuft und pro Windung in jeder Spule den gleichen Wert hat. Deshalb gilt unabhängig von der Kurvenform:

$\frac{U_\mathrm{p}}{U_\mathrm{s}}=\frac{n_\mathrm{p}}{n_\mathrm{s}}$

Betrieb mit Frequenzgemisch

Der Abstand f₂ bis f₁ heißt Bandbreite

In diesem Artikel werden nur Breitbandtrafos behandelt, die – wie Audiotransformatoren – ein Frequenzgemisch von f₁ = 50 Hz bis f₂ = 20 kHz übertragen müssen (Dreieckspannung ist auch ein Frequenzgemisch). Dabei ändert sich die Impedanz der Primärspule im gleichen Verhältnis 20000/50 = 400, was dazu führt, dass bei tiefen Frequenzen der ohmsche und bei hohen Frequenzen der induktive Anteil am Gesamtwiderstand überwiegt.

• Bei tiefen Frequenzen ist der Primärstrom eingeprägt, der Trafo differenziert. Das bedeutet zum einen eine Phasenverschiebung von etwa 90° zwischen Ein- und Ausgangsspannung, zum anderen sinkt die induzierte Sekundärspannung proportional zur Frequenz. Für eine möglichst tiefe Grenzfrequenz muss die Primärspule möglichst viele Windungen haben, damit die Impedanz ausreichend groß bleibt.
• Bei mittleren Frequenzen überträgt der Trafo die Kurvenform 1:1, da mit eingeprägter Spannung gearbeitet wird. Die Phasenverschiebung beträgt etwa 0°.
• Bei hohen Frequenzen macht sich immer stärker der Einfluss der Wicklungskapazität bemerkbar, der den Wechselstrom nicht durch die Spule, sondern zunehmend durch die parallel liegende, unvermeidbare Kapazität fließen lässt. Zusammen können beide einen Schwingkreis bilden, der einen schmalen Frequenzbereich bevorzugt. Dieser liegt um so tiefer, je mehr Windungen die Spule besitzt. Es treten wieder deutliche Phasenverschiebungen auf.

Die Forderungen für hohe und tiefe Grenzfrequenz widersprechen sich, deshalb sind Breitbandtrafos schwierig zu bauen.

Betrieb mit einer Rechteckspannung

Strom I_L durch die Spule nach dem Einschalten an eine Gleichspannung als Funktion der Zeit

Sättigungsmagnetisierung eines Eisenkerns. rot=Primärspannung, blau=Sekundärspannung

Prinzip des Sperrwandlers

Spannungen und Ströme beim Sperrwandler

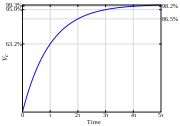
In Schaltnetzteilen werden Trafos immer mit rechteckförmigen Spannungsverläufen versorgt, weil dadurch die Verlustleistung in den elektronischen Schaltern (Transistoren) sehr gering sind. Die Spannung wird von Kondensatoren mit geringen Innenwiderständen bereitgestellt, deshalb liegt hier Betrieb mit eingeprägter Spannung vor. Wenn durch die Primärspule vorher kein Strom geflossen ist, steigt dieser nach dem Einschalten immer nach der gleichen Gesetzmäßigkeit an, die im nebenstehenden Bild dargestellt ist: Zunächst schnell, dann langsamer und schließlich strebt der Strom dem Grenzwert U_prim/R zu, wobei R der ohmsche Widerstand der Primärwicklung ist. Dann ist das Magnetfeld zwar sehr stark, es ändert sich aber nicht mehr und deshalb sinkt die induzierte Spannung auf Null. Weit vorher muss der Strom abgeschaltet werden, um den Transistor nicht zu gefährden und den Eisenkern nicht in die Sättigungsmagnetisierung zu treiben.

Im nebenstehenden Bild wird deutlich vor dem Zeitpunkt, an dem die rot dargestellte Wechselspannung periodisch umgepolt wird, der Eisenkern gesättigt. Obwohl die Spannung weiterhin anliegt und der Primärstrom stark ansteigt (nicht aufgezeichnet), wird die induzierte Spannung (blau dargestellt) zu Null, weil die Änderung des Magnetfeldes dΦ auch Null wird. Bei höherer Frequenz und entsprechend kürzerer Einschaltdauer wäre dieser Effekt nicht aufgetreten. Die Spannungszeitfläche der angelegten Spannungshalbwelle ist hier größer als die für welche der Trafo ausgelegt ist. (Windungszahl und oder Eisenfläche sind zu klein.)

Als Beispiel wird angenommen, dass als Primärspule zehn Windungen dicker Kupferdraht auf einen Ferrit-Kern mit der Kennzahl A_L = 1200 nH gewickelt werden. Diese Spule hat die Induktivität 120 µH und wird über einen Schalttransistor Q mit einem Kondensator verbunden, der auf 300 V aufgeladen ist. Mit einem Gesamtwiderstand der Reihenschaltung dieser Bauelemente von 1 Ω ergibt sich die Zeitkonstante T = 120 µs. In dieser Zeit steigt der Strom fast linear an und erreicht 63,2 % des Endwertes 300 A. Wenn der Schalttransistor 19 A aushält, darf er also nur 12 µs lang bis t₁ eingeschaltet sein. Während dieser Zeit entnimmt er dem Kondensator die Energie E = 0,5·L·J² = 22 mWs.

Sperrwandler

Diese Energie wird beim Sperrwandler während der Einschaltphase 0...t₁ als magnetische Feldenergie in der Speicherdrossel mit Luftspalt gespeichert und nach dem Abschalten des Transistors ähnlich wie bei einem Funkeninduktor als Spannungsimpuls an der Sekundärspule abgenommen. In Netzgeräten oder bei Elektronenblitzgeräten lädt man mit dieser Energie einen Kondensator C (rechts im Bild) auf. Dabei gibt es kein festes Spannungsübersetzungsverhältnis nach der Form U_p/U_s = N_p/N_s, sondern die Sekundärspannung springt schlagartig auf auf die Spannung, die der Kondensator (noch) hat, weil die Primärspannung ebenfalls nicht in ihrer Höhe definiert ist nach dem Abschalten. Dadurch wird der Gleichrichter D leitend und es fließt von t₁ bis t₂ Strom, der den Kondensator C auflädt. Wenn die gespeicherte magnetische Energie auf den Kondensator übertragen wurde, bricht die Sekundärspannung und die Primärspannung zusammen und nach einer kurzen Pause kann auf die Primärspule ab T der nächste Stromimpuls gegeben werden. Wichtig ist es zu wissen, dass die zu übertragende Energie nur im Luftspalt zwischen gespeichert wird, (Spannung mal Strom mal Zeit), weshalb solche Übertrager alle einen definierten Luftspalt haben müssen.

Die Energiezufuhr bewirkt beim Kondensator eine Spannungserhöhung, die sich mit der Gleichung E = 0,5·C·U² berechnen lässt. Durch Differenzieren erhält man ΔE = C·U·ΔU. Wenn ein 2000 µF-Kondensator (noch) auf 12 V aufgeladen ist, erzeugt der nächste Energieimpuls von 22 mWs einen Spannunganstieg um ΔU = 0,9 V.

Im Dauerbetrieb muss der mittlere Magnetische Fluss Φ konstant sein, deshalb muss die Spannungszeitfläche zwischen 0 und t₁ genauso groß sein wie zwischen t₁ und t₂. Zunächst wird die Primärspule über den Schalttransistor t₁ = 12 µs lang an 300 V gelegt, anschließend liefert die Sekundärspule während der Zeitdauer t₂-t₁ die Spannung 13 V an den 2000 µF-Kondensator (Spannungsverlust am Gleichrichter nicht vergessen!). Daraus folgt

$300\, V\cdot 12\,\mu s = 13\,V\cdot(t_2-t_1)$

mit der Lösung t₂-t₁ = 280 µs. Wegen I·(t₂-t₁) = C·ΔU lässt sich der mittlere Ladestrom 6,5 A des Kondensators ermitteln. Wie im Bild zu sehen ist, sinkt er in diesem Zeitraum vom Anfangswert 13 A etwa linear auf Null.

Beim Sperrwandler gilt - wie bei jedem Trafo - dass die induzierte Spannung pro Windung in allen Wicklungen gleich ist. (Auch die Kurvenform der Spannung.) Wenn im Zeitraum t₂-t₁ an der Sekundärspule 13 V anliegt, erscheint diese Spannung mit dem entsprechenden Transformationsverhältnis ü = N_s/N_p = U_s/U_p auch an der Primärwicklung und muss zur Betriebsspannung addiert werden („Rücktransformation“). Wenn im vorliegenden Beispiel ü = 0,1 gewählt wird, steigt die Spannung am Transistor während der Ladezeit des Kondensators auf

$U_{max}=300\,V+\frac{13\,V}{0,1}=430\,V$

Durchflusswandler

Hier findet keine Zwischenspeicherung der Energie im Eisenkern statt, sondern während der gesamten Einschaltphase des Transistors wird Energie an den Sekundärkreis übertragen. Der Eisenkern darf keinen Luftspalt besitzen, die Hysteresekurve soll schmal sein. Auch hier gilt - wie bei jedem Trafo - dass die induzierte Spannung pro Windung in allen Wicklungen gleich ist. Wenn im Zeitraum 0 bis t₁ 300 V an die Primärspule gelegt werden und gleichzeitig an der Sekundärspule 13 V erwartet werden, muss das Transformationsverhältnis ü = N_s/N_p = U_s/U_p = 13 V/300 V = 0,043 betragen.

Wird der Transformator mit Rechteckspannung betrieben, ist ein Eisenkern fast zwingend erforderlich, denn ohne einen solchen würde man sehr viele Windungen für eine ausreichend große Induktivität L benötigen und der ohmsche Widerstand der Spule wäre recht groß. Dadurch würde die Zeitkonstante L/R viel kleiner sein als im obigen Beispiel und auch die schnellsten Schalttransistoren würden zu langsam schalten.

Skin- und Proximity-Effekt

Der Skin-Effekt tritt vorwiegend bei hohen Signalfrequenzen in Erscheinung. Er bewirkt, dass nur noch das Äußere des Leiters zum Stromfluss beiträgt. Der Skin-Effekt beruht auf der Abschirmungswirkung elektrisch leitfähiger Materialien gegenüber elektromagnetischen Feldern. Nach Küpfmüller, Mathis, Reibiger: Theoretische Elektrotechnik ist dieser Effekt nicht, wie häufig beschrieben, auf Wirbelströme zurückzuführen. Vielmehr handelt es sich um eine Felddiffusion in den Leiter, bei der die Eindringtiefe begrenzt ist und somit ein Eindringmaß definiert werden kann. Ein metallischer magnetisch neutraler Leiter wirkt für Hochfrequenzfelder wie ein magnetisch undurchlässiger Stoff mit der Permeabilität null. Der Skin-Effekt kann durch die Verwendung von Hochfrequenzlitze verringert werden. Bei HF-Litze wird ein Leiter durch die Parallelschaltung von gegeneinander elektrisch isolierten und miteinander verwobenen Einzelleitern ersetzt.

Der Proximity-Effekt beruht auf der Wechselwirkung des Stromes mit den elektromagnetischen Feldern benachbarter Leiter. Insbesondere dann, wenn benachbarte Leiter entgegengesetzt gerichtete Ströme aufweisen, sorgt der Proximity-Effekt für eine verminderte effektive Querschnittsfläche des Leiters.^[1]

Betrieb mit einer Sinusspannung

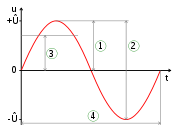Eine sinusförmige Wechselspannung.
1 = Scheitelwert,
2 = Spitze-Spitze-Wert,
3 = Effektivwert,
4 = Periodendauer

Wird die Primärspule an eine sinusförmige Wechselspannung angeschlossen, werden die notwendigen Gleichungen komplizierter. Die Funktion eines Trafos kann (zu) einfach - und falsch! - so erklärt werden: Der durchfließende Wechselstrom I_primär erzeugt im Inneren der Spule mit N_primär Windungen und der Länge l folgende magnetische Flussdichte:

$B= \mu_r \cdot \mu_0 \cdot \frac{N}{l} \cdot I$

wobei μ₀ die Magnetische Feldkonstante und μ_r die Permeabilitätszahl sind. Dieses Magnetfeld ändert sich wie der Strom und induziert in der Sekundärspule eine Wechselspannung, die von der Windungszahl abhängt, wie weiter oben beschrieben.

Diese Erklärung hat einige Mängel: Sie berücksichtigt nicht, dass Trafos üblicherweise mit vorgegebener („eingeprägter“) Spannung, beispielsweise 230 V, betrieben werden und nicht mit vorgegebenem Strom I, den die Gleichung verlangt. Aus ihr folgt nicht, wieso bei tiefen Frequenzen ein Eisenkern erforderlich ist. Sie liefert weder einen Anhaltspunkt für den einfachen Zusammenhang U_p/U_s =  N_p/N_s noch für experimentellen Befund, dass sich der Primärstrom bei unterschiedlicher Belastung auf der Sekundärseite stark und fast proportional ändert.

Diese belastungsabhängige Stromaufnahme liefert den Schlüssel für die korrekte Erklärung. Es muss einen Effekt geben, der dafür sorgt, dass der aufgenommene Strom immer geringer ist als der Maximalwert, der sich nach dem ohmschen Gesetz aus der angelegten Wechselspannung (230 V) und dem Widerstand der Primärspule eines zum Beispiel 100VA Trafos (etwa 5 Ω) ergibt. Im Leerlauf, also ohne sekundärseitige Belastung, kann der Primärstrom auf einige Prozent des Nennstromes von hier 0,43A sinken. Dieser Effekt wird durch die Selbstinduktion verursacht, er soll hier nicht im Detail diskutiert werden. Kurz zusammengefasst geschieht im eingeschwungenen Zustand, also nicht in den ersten Augenblicken nach dem Einschalten, folgendes:

• Die angelegte Wechselspannung U_Netz lässt in der Primärspule einen Wechselstrom fließen, der im Eisenkern ein magnetisches Wechselfeld erzeugt.
• Dieses induziert in allen Spulen des Trafos, also auch in der Primärspule eine „Gegenspannung“ U_induziert, die fast so groß ist wie die angelegte Wechselspannung und diese weitgehend kompensiert (Lenzsche Regel). Als „Antriebsspannung“ für den Primärstrom steht nur die Differenzspannung U_Netz - U_induziert zur Verfügung, die wenige Volt beträgt und am ohmschen Widerstand des Spulendrahtes abfällt. Deshalb ist der Primärstrom so gering.
• Wäre die Gegenspannung zu gering, würde die Differenzspannung U_Netz - U_induziert sofort größer werden und höheren Primärstrom fließen lassen. Dadurch würde aber das Magnetfeld ansteigen und mehr Gegenspannung erzeugen. Dieses Verhalten nennt man dynamisches stabiles Gleichgewicht. Es sorgt in jedem Moment dafür, dass die induzierte Spannung "parallel" zur angelegten Wechselspannung mitläuft.

Das ist auch die Begründung für die Gleichung

$\frac{U_p}{U_s}=\frac{n_p}{n_s}$

zur Berechnung der Windungszahlenverhältnisses, um die Sekundärspannung U_s zu erhalten. Wenn die „Gegenspannung“ U_induziert in der Primärspule fast so groß ist wie die angelegte Wechselspannung U_p, gilt das genauso für die induzierte Spannung U_s in einem parallel mitgeführten Draht, der nun Sekundärspule genannt wird. Das ändert sich auch nicht, wenn die Drähte nicht exakt nebeneinander liegen, sie können sogar in merklicher Entfernung montiert werden, solange sie vom gleichen Magnetfeld durchflossen werden. Und wenn man die Windungszahl halbiert, erhält man auch nur die halbe Spannung. Mit der Gleichung

$U_p=N_p\cdot \frac{\mathrm{d}B}{\mathrm{d}t}\cdot A$

aus dem vorhergehenden Absatz und der maximalen Flussdichte B = 1,7 T für kornorientiertes Dynamoblech kann man die induzierte Spannung pro Windung abschätzen. Da sich die Netzspannung in dt = 5 ms von Null bis zum Maximalwert U_max ändert, gilt für einen Eisenkern der Querschnittsfläche 10 cm² mit guter Näherung

$U_{eff}=1\cdot \frac{1,7\, T}{0,005\, s}\cdot 10\, cm^2=0,34\,V$

Das Ergebnis ist nicht ganz exakt, weil bei dieser Gleichung nicht die Sinusform der Netzspannung berücksichtigt ist. Die genaue Gleichung findet man hier.

Der Eisenkern

Die Verwendung eines Eisenkerns verringert zwar die Anzahl der notwendigen Windungen in beiden Spulen, bringt aber auch Nachteile mit: Der Eisenkern kann magnetisch gesättigt werden, dann wird die transformierte Wechselspannung verzerrt. Ferner entstehen im Eisen Wirbelstromverluste. Je tiefer die zu übertragende Frequenz ist, desto zwingender ist aber die Verwendung eines Eisenkerns. Das wird am Beispiel eines 50 Hz-Trafos erläutert.

Netztrafo ohne Eisenkern

Der Eisen- oder Ferritkern im Trafo ist überflüssig, wenn

1. der induktive Widerstand Z_L = 2πf·L der Primärspule bei der Betriebsfrequenz f so hoch ist, dass ein akzeptabler, das heißt nur geringer Leerlaufstrom fließt und
2. der ohmsche Widerstand der Spule so gering ist, dass der Draht auch bei Höchstlast des Trafos, also bei maximalem Primärstrom, nicht überhitzt wird.

Bei Frequenzen über 1 MHz genügen meist weniger als 100 Windungen, um beide Forderungen zu erfüllen. Bei tiefer Frequenz treten unüberwindbare Probleme auf, wie folgendes Beispiel für einen Netztrafo von 100 W und bescheidener Qualität zeigt: Für einen Leerlaufstrom von 100 mA muss Z_L = 2300 Ω und L = 7,3 H sein. Die erforderliche Windungszahl N der Primärspule kann man mit der Gleichung

$L = N^2 \cdot \frac{\mu_0 \mu_r A}{l}$

abschätzen und erhält ohne Eisenkern etwa 31000 Windungen mit einer Drahtlänge von 10 km und einem Maximalwiderstand von 40 Ω. Der notwendige Kupferdraht müsste einen Querschnitt von 4,3 mm² haben, der bei 31000 Windungen einen Wicklungsquerschnitt von 1300 cm² einnimmt. In diese Primärspule müsste eine etwa gleich massive Sekundärspule „eingewoben“ werden, um eine gute magnetische Kopplung zu erzielen. Insgesamt ergibt sich ein Gesamtvolumen von etwa einem Kubikmeter bei 9000 kg Masse.

Netztrafo mit Eisenkern

(siehe auch Eisenkerntransformator)

Dieser ohne Eisenkern kaum realisierbare Trafo lässt sich mit einem ausreichend großen Kern aus Dynamoblech auf handliche Werte verkleinern. Wegen der sehr hohen Permeabilitätszahl µ_r von etwa 2000 genügen nun 700 Windungen für die Primärspule. An Stelle eines massiven Eisenkerns muss dünnes Trafoblech eingesetzt werden, um die Wirbelströme im Kern gering zu halten.

Wählt man für den 100 W-Trafo einen (zu) großen Eisenkern von 10 kg, gibt es kein Problem mit der Sättigungsmagnetisierung. Je kleiner und leichter aber der Eisenkern sein soll, desto weniger Weiss-Bezirke enthält er. Diese werden aber bereits bei geringeren Magnetfeldern komplett ausgerichtet - Sättigung ist erreicht. Das erzeugt eine Reihe von neuartigen Problemen: Verzerrungen der Sinusform des Leerlaufstromes, zusätzliche Wärme und massive Stromspitzen beim Einschalten.

Ausschnitt der Hysteresekurve mit unterschiedlichen Stromdifferenzen bei konstanter Φ-Änderung an einem großen Trafo

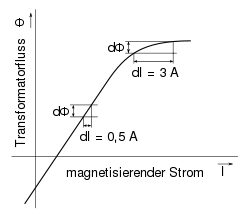
Der Reihe nach: Bei Induktion dreht sich alles um die Gleichung U = dΦ/dt mit dem „Magnetfluss“ Φ  = B·A. Bei jedem Trafo ist die Spulenfläche A konstant, deshalb muss das Magnetfeld B geändert werden. B wird von der Primärspule erzeugt, dafür gilt die Gleichung B = μ_r·μ₀·H = μ_r·μ₀·J·N/l. Vereint man diese Gleichungen und fasst dabei alle uninteressanten (konstanten) Faktoren in f zusammen, erhält man B = μ_r·f·J. Das sollte eine Gerade mit dem Steigungsfaktor μ_r sein, die immer weiter ansteigt. Im Experiment gilt das nur für kleine Ströme, bei großen Strömen biegt die Gerade nach rechts ab. μ_r ist leider nicht konstant, sondern wird mit steigendem Strom J immer kleiner, sinkt bis zum Wert 1. Im nebenstehenden Bild sieht man, dass man nicht immer den gleichen Stromzuwachs dJ benötigt, um den Magnetfluss Φ um den gleichen Betrag dΦ zu vergrößern. Genügt anfangs ein Stromzuwachs von 0,5 A für eine gewisse Flussänderung, benötigt man bei höherem Gesamtstrom bereits 3 A oder mehr, um die gleiche Flussänderung zu erzielen.

An dieser Stelle gibt es natürliche Grenzen: Jedes Stück Eisen besteht aus endlich vielen Atomen, die nur eine gewisse Anzahl Weiss-Bezirke bilden können. Deren Orientierung zeigt ohne externes Magnetfeld - statistisch verteilt - in alle Richtungen, das Eisen ist entmagnetisiert. Mit zunehmendem Strom durch die Primärspule werden immer noch mehr Bezirke parallel zur Spulenachse ausgerichtet und die Kurve steigt steil an. Wenn aber fast alle orientiert sind, hilft auch kein weiterer Stromanstieg, um noch mehr in diese Richtung zu zwingen, denn es sind ja keine mehr da. Der Magnetfluss kann kaum noch steigen, die Kurve wird flacher. Bei kornorientiertem Dynamoblech geht man bis zu Flussdichten B = 1,6…1,75 T; Sättigung tritt ein ab 2,03 Tesla.

Für den Primärstrom hat das katastrophale Folgen: Sobald die Hysteresekurve flach wird, kann Φ kaum noch ansteigen, die Änderung dΦ wird Null. Da deshalb die Gegenspannung U_induziert auch verschwindet, steigt der Primärstrom auf extreme Werte (Einschalten des Transformators), bis die Sicherung abschaltet. Ein gesättigter Kern hat die gleiche Wirkung wie Luft, nämlich keine. Der Strom wird dann nur durch den ohmschen Widerstand der Primärspule begrenzt.

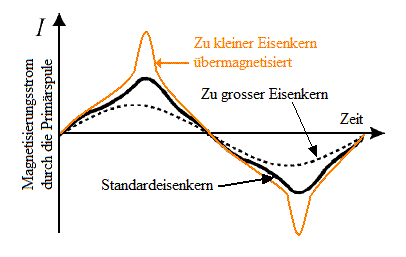
Der Magnetisierungsstrom

Verlauf des Magnetisierungsstromes bei unterschiedlichen Eisenkerngrößen, desselben Kerntyps bei gegebenem Magnetfluss

Der Querschnitt A des Eisenkerns ist ein Maß dafür, wie viele Weiss-Bezirke vom gegebenen Magnetfeld der Primärspule ausgerichtet werden können. Der Kern wird im Bild verkleinert oder vergrößert. Sind alle Weiss-Bezirke parallel zur Spulenachse orientiert (magnetische Sättigung), kann sich Φ nicht mehr ändern, die Selbstinduktion kann keine Gegenspannung mehr induzieren und der Strom durch die Primärspule steigt steil an (rote Kurve im Bild). Gleichzeitig strebt die Spannung in der Sekundärspule gegen Null - das ist unerwünscht! In diesem Moment wird besonders viel Energie aus dem Stromnetz entnommen und wenig an die Sekundärspule übertragen. Als Folge kann die Primärspule durchbrennen.

Übliche Gegenmittel: Entweder den Eisenkern vergrößern oder die Frequenz erhöhen oder beides oder mehr Windungen draufpacken. Wer jemals einen 300 W-Netztrafo gehoben und mit dem Gewicht eines Computernetzteils gleicher Leistung verglichen hat, weiß, was man mit ausreichend hoher Frequenz von etwa 50 kHz erreichen kann. Die Begründung steckt wieder in der Gleichung für die Windungsspannung.

$U_{ind}=\frac{\mathrm{d}B}{\mathrm{d}t}\cdot A=\frac{\mathrm{d}B\cdot A}{\mathrm{d}t}= \frac{\mathrm{d}B \cdot 0,1\cdot A}{0,1\cdot\mathrm{d}t}=\frac{\mathrm{d}B\cdot A_1}{\mathrm{d}t_1}$

Wird die Frequenz verzehnfacht, dauert eine Schwingung nur noch 0,1·dt. Verringert man die Spulenfläche A ebenfalls um den Faktor 10 auf A₁, entsteht die gleiche Induktionsspannung. Wenn aber die Eisenfläche auf 10 % verringert wird, schrumpfen bei Einhaltung der Proportionen alle Abmessungen und sowohl Volumen als auch Masse des Trafos verringern sich auf 3,2 % des ursprünglichen Wertes. Aus diesem Grund wurde für das Bordnetz von Flugzeugen die Frequenz 400 Hz gewählt. Umgekehrt benötigen Trafos für Bahnstrom bei der Frequenz 16,7 Hz die dreifache Eisenfläche und die 5,2-fache Masse im Vergleich zum Betrieb mit 50 Hz.

Zu speziellen Problemen beim Einschalten von Transformatoren siehe Einschalten des Transformators

Streufluss

Linker Teil eines aufgeschnittenen Streufeldtrafos

Streufluss eines Trafokerns

Bei einem idealen Transformator würden alle Linien des Magnetflusses, die von der Primärspule erzeugt werden, auch durch die Sekundärspule laufen. Bei einem realen Trafo schlagen einige Magnetfeldlinien andere Wege ein, insbesondere bei geringer Permeabilität des Magnetwerkstoffes und hoher Belastung „weichen“ sie der Sekundärwicklung aus. Das erzeugt unerwünschte Magnetfelder in der Umgebung, die in manchen Geräten wie Oszilloskopen sehr störend sein können und besondere Abschirmungen verlangen. Außerdem verringern sie den Wirkungsgrad des Trafos und sorgen dafür, dass die Gleichung N_p/N_s=U_p/U_s nicht genau gilt. Abhilfe sind geringe Abstände zwischen Wicklung und Eisenkern sowie Vermeiden von räumlich getrennten Spulen.

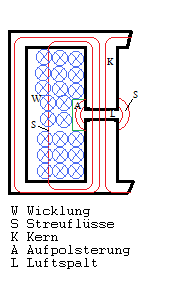
Es gibt aber Einsatzbereiche, bei denen das Streufeld erwünscht ist, wie Streufeldtransformatoren beim Schweißen oder als Vorschaltgeräte für Leuchtstoffröhren. In diesen Fällen werden gezielt Luftspalte eingebaut, wie im nebenstehenden Bild zu sehen ist. Der Streufeldtransformator vereint die Funktion eines Transformators (Spannungstransformation und galvanische Trennung) und einer strombegrenzenden Drossel in einem Bauteil.

Laminierte Blechpakete

Wirbelströme im Eisenblock (oben) und in laminierten Blechen (unten)

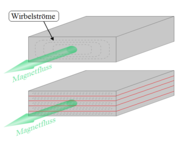
Ein massiver Eisenkern würde in der Primärwicklung wie eine kurzgeschlossene Windung wirken, in der ein großer Strom induziert wird. Obwohl die Leitfähigkeit von Eisen nicht besonders gut ist, würde darin sehr viel Wärmeenergie entstehen. Das ist beim Induktionskochfeld und Induktionsofen erwünscht, muss aber beim Trafo vermieden werden. Aus diesem Grund wird der Kern eines Trafos aus dünnen, voneinander isolierten Dynamoblechen zusammengesetzt, damit die Fläche A quer zum Magnetfluss Φ gering wird. Dann bleibt die induzierte Spannung wegen

$U_{ind}=A\cdot \frac{\mathrm{d}B}{\mathrm{d}t}$

auch bei starken Änderungen des Magnetfeldes B klein und damit auch die erzeugte Wärme.

Bei hoher Frequenz wird die Zeit dt immer kleiner, das muss durch dünneres Blech kompensiert werden. Kerne von NF-Trafos sind immer aus besonders dünnen Eisen-„Folien“ aufgebaut. Das reicht bei noch höheren Frequenzen nicht aus, dort geht man zu Ferritkernen oder Ringkernen aus gepresstem Eisenpulver über. (siehe auch Wirbelstrom#Nachteilige Wirkung von Wirbelströmen)

Widerstandstransformation

Bei Leistungsanpassung muss der Belastungswiderstand den gleichen Wert haben wie der Innenwiderstand der Stromquelle. Bei unterschiedlichen Werten kann - bei Wechselstrom - ein Transformator zur Widerstandsanpassung verwendet werden. Zur Herleitung des Zusammenhangs multipliziert man die beiden linken Seiten und die rechten Seiten der Formeln

$\frac{U_{p}}{U_{s}}=\frac{N_{p}}{N_{s}} \qquad \text{und} \qquad \frac{I_{s}}{I_{p}} = \frac {N_{p}}{N_{s}}$

und erhält

$\frac{U_{p}}{U_{s}} \cdot \frac{I_{s}}{I_{p}} =\left( \frac{N_{p}}{N_{s}} \right)^2$

Zusammen mit dem ohmschen Gesetz R = U/I folgt daraus

$\frac{R_p}{R_s} = \left( \frac{N_p}{N_s} \right)^2$

Durch ein Windungszahlverhältnis von 1:2 wird eine Widerstandstransformation von 1:4 erreicht. Beispiele:

• Die sehr geringe Spannung eines Bändchenmikrofons mit dem Innenwiderstand von nur 0,2 Ω muss auf 180 Ω angehoben werden, damit das Signal störungsarm übertragen werden kann. Aus dem Widerstandsverhältnis 900 folgt ein Übersetzungsverhältnis von 30 für den Trafo. Dadurch wird auch die induzierte Spannung des Mikrofons um den Faktor 30 heraufgesetzt.
• Ein Lautsprecher mit R = 4 Ω soll an eine Röhrenendstufe der Impedanz von 2000 Ω angepasst werden. Dann muss der Trafo ein Übersetzungsverhältnis von

$a=\sqrt {\frac{2000}{4}} = 22$

haben. Die Verwendung eines Trafos hat den erwünschten Nebeneffekt, dass durch den Lautsprecher kein Gleichstrom fließen kann.

Einzelnachweise

1. ↑ http://www.tu-dresden.de/etieeh/Lehre/vorlesungen_eet/Hochspannungsgeraete/G7.pdf

Siehe auch

• Resonanztransformator
• Streufeldtransformator

Weblinks

• Versuche und Aufgaben zum Transformator