- Algorithmus von Hierholzer
-
Der Algorithmus von Hierholzer ist ein Algorithmus aus dem Gebiet der Graphentheorie mit dem man in einem ungerichteten Graphen Eulerkreise bestimmt. Er geht auf Ideen von Carl Hierholzer zurück.
Voraussetzung: Sei G = (V,E) ein zusammenhängender Graph, der nur Knoten mit geradem Grad aufweist.
- Wähle einen beliebigen Knoten v0 des Graphen und konstruiere von v0 ausgehend einen Unterkreis K in G, der keine Kante in G zweimal durchläuft.
- Wenn K ein Eulerkreis ist, breche ab. Andernfalls:
- Vernachlässige nun alle Kanten des Unterkreises K.
- Am ersten Eckpunkt von K, dessen Grad größer 0 ist, lässt man nun einen weiteren Unterkreis K' entstehen, der keine Kante in K durchläuft und keine Kante in G zweimal.
- Füge in K den zweiten Kreis K' ein, indem der Startpunkt von K' durch alle Punkte von K' in der richtigen Reihenfolge ersetzt wird.
- Nenne jetzt den so erhaltenen Kreis K und fahre bei Schritt 2 fort.
Die Komplexität des Algorithmus ist linear in der Anzahl der Kanten.
Beispiel
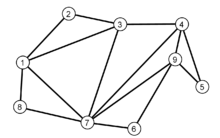
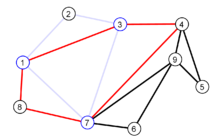
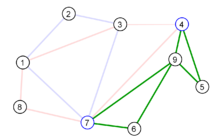
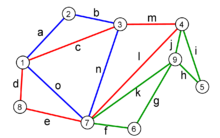
Gegeben sei ein Eulergraph mit neun Knoten (siehe erste Abbildung). Ein Zyklus vom Startknoten 1 wäre beispielsweise die in der zweiten Abbildung blau dargestellte Knotenfolge Cblau = (1,2,3,7,1). Nach Entfernen dieser Kanten haben die Knoten 1, 3 und 7 der bisher gebildeten Zykel noch einen Knotengrad größer Null, welche als Startknoten für den nächsten Zyklus in Frage kommen. Vom Startknoten 3 aus kann man den Kreis Crot = (3,1,8,7,4,3) bilden (in der dritten Abbildung rot). Wählt man nun als Startknoten den Knoten 7, kann man von den übrig gebliebenen Kanten den Zykel Cgruen = (7,6,9,5,4,9,7) bilden. Setzt man jetzt Cgruen in Crot an Stelle des Knoten 7 ein, erhält man den Zykel (3,1,8,7,6,9,5,4,9,7,4,3). Setzt man diesen in Cblau an Stelle des Knoten 3 ein, erhält man die mögliche Eulertour (1,2,3,1,8,7,6,9,5,4,9,7,4,3,7,1) wie in der letzten Abbildung gezeigt.
Literatur
- Sven Oliver Krumke, Hartmut Noltemeier: Graphentheoretische Konzepte und Algorithmen. Teubner, Wiesbaden 2005, ISBN 3-519-00526-3, S. 45−48
Weblinks
Wikimedia Foundation.