Haarscher Raum

Ein Haar-Raum, oder Haarscher Raum (benannt nach Alfred Haar) wird in der Approximationstheorie folgendermaßen definiert:

Besitzen n linear unabhängige, auf einem Intervall [a,b] stetige Funktionen 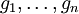$g_1,\dots,g_n$ die Eigenschaft, dass jedes Element 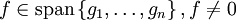${f}\in \mathrm{span}\left\{g_1,\dots,g_n\right\}, f \neq 0$, in [a,b] höchstens (n − 1) Nullstellen hat, dann heißt die Menge 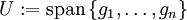$U:= \mathrm{span}\left\{g_1,\dots,g_n\right\}$ Haar-Raum.

Ein System solcher Funktionen 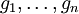$g_1,\dots,g_n$, die einen Haar-Raum aufspannen, wird auch Haarsches System oder Tschebyschow-System genannt. Wird eine stetige Funktion durch Elemente eines Haar-Raumes approximiert, so existiert bezüglich der Maximumsnorm 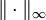$\|\cdot\|_\infty$ stets eine beste Approximation.

Interpolation in Haar-Räumen

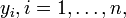Hat man $x_1, \dots, x_n \in [a, b]$ paarweise verschiedene Punkte (Stützstellen) und Daten $y_i, i = 1, \dots, n,$, so existiert genau ein 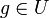$g \in U$ mit $g(x_i) = y_i, i=1, \dots, n$.

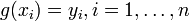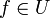Beweis Die Abbildung $L: U \to [a, b]^n, f \to (f(x_1), ...f(x_n))$ ist linear. Weil jedes $f \in U$ höchstens n-1 Nullstellen hat, ist der Kern der Abbildung nur die Nullfunktion, d.h. L ist injektiv. Wegen dim[a,b]ⁿ = n ist L surjektiv, also insgesamt bijektiv. Daraus folgt Existenz und Eindeutigkeit der Interpolationsfunktion g.

Beispiele

• Der Vektorraum Π_n der Polynome höchstens n-ten Grades ist ein Haar-Raum. 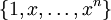$\left\{1,x,\dots,x^n\right\}$ ist ein Haarsches System.
• Die trigonometrischen Polynome bilden ein Haar-Raum mit Haarschem System 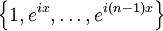$\left\{1,e^{ix},\dots,e^{i(n-1)x}\right\}$ (Polynome in e^ix).
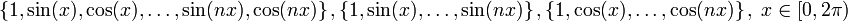• $\left\{1,\sin (x),\cos (x),\dots,\sin (nx),\cos (nx) \right\}, \left\{1,\sin (x),\dots,\sin (nx) \right\}, \left\{1,\cos (x),\dots,\cos (nx) \right\},\; x \in [0,2\pi)$ sind jeweils Haarsche Systeme.

Literatur

• Günther Hämmerlin, Karl-Heinz Hoffmann: Numerische Mathematik. Springer, Berlin 1994, ISBN 3-540-58033-6