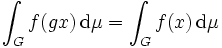Haarsches Mass

Das Haarsche Maß wurde von Alfréd Haar in die Mathematik eingeführt, um Ergebnisse der Maßtheorie in der Gruppentheorie anwendbar zu machen.

Es ist eine Verallgemeinerung des Lebesgue-Maßes. Das Lebesgue-Maß ist ein Maß auf dem euklidischen Raum das unter Translationen invariant ist. Der euklidische Raum ist eine lokalkompakte topologische Gruppe bezüglich der Addition. Das Haarsche Maß ist für jede lokalkompakte topologische Gruppe definierbar, insbesondere also für jede Lie-Gruppe.

Definition

Das (linke) Haarsche Maß einer lokalkompakten Gruppe ist das bis auf einen Faktor eindeutig bestimmte linksinvariante reguläre Borelmaß, das auf nichtleeren offenen Teilmengen positiv ist.

Ein Maß μ heißt dabei linksinvariant, wenn

$\int_G f(gx)\,\mathrm d\mu=\int_G f(x)\,\mathrm d\mu$

für stetige Funktionen f und Gruppenelemente g gilt.

Ersetzt man "linksinvariant" durch den analogen Begriff "rechtsinvariant", erhält man den Begriff des rechten Haar-Maßes. Stimmen sie überein, so heißt die Gruppe unimodular. Abelsche Gruppen sowie kompakte Gruppen sind unimodular.

Eigenschaften

Das Haarsche Maß einer lokalkompakten topologischen Gruppe ist genau dann endlich, wenn die Gruppe kompakt ist. Diese Tatsache ermöglicht es, eine Mittelung über unendliche kompakte Gruppen durch Integration bezüglich dieses Maßes durchzuführen. Eine Folge ist beispielsweise, dass jede endlichdimensionale komplexe Darstellung einer kompakten Gruppe unitär bezüglich eines geeigneten Skalarproduktes ist.