- Hausdorffmetrik
-
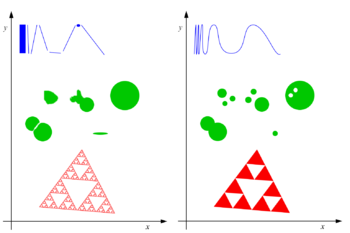
Die gefärbten Mengen links haben verhältnismäßig geringen Hausdorff-Abstand zu den entsprechenden Mengen rechts.Die Hausdorff-Metrik, benannt nach dem Mathematiker Felix Hausdorff, misst den Abstand δ(A,B) zwischen nichtleeren kompakten Teilmengen A, B eines metrischen Raums E.
Anschaulich haben zwei kompakte Teilmengen umso geringeren Hausdorff-Abstand, je besser sie einander wechselseitig überdecken.
Definition
Als Hilfsmittel definiert man den Abstand D zwischen einem Punkt x und einer nichtleeren kompakten Teilmenge K ⊆ E unter Rückgriff auf die Metrik d des Raums E als
- D(x,K):=min {d(x,k) | k∈K}.
Dann definiert man den Hausdorff-Abstand zwischen zwei nichtleeren kompakten Teilmengen A und B als
- δ(A,B):= max {max{D(a,B) | a∈A} , max{D(b,A) | b∈B} }.
Man kann zeigen, dass δ in der Tat eine Metrik auf der Menge aller kompakten Teilmengen von E ist.
Anwendungen
In der Theorie der iterierten Funktionensysteme werden Fraktale als Folgengrenzwerte im Sinne der Hausdorff-Metrik erzeugt.
Siehe auch
Wikimedia Foundation.
