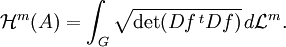- Hausdorffmaß
-
Zur Bestimmung des Flächeninhalts einer m-dimensionalen Fläche im n-dimensionalen Raum
 (mit m < n) gibt es in der Maßtheorie diverse Maße, die für alle Teilmengen des
(mit m < n) gibt es in der Maßtheorie diverse Maße, die für alle Teilmengen des  definiert sind und auf den „anständigen“ (nicht entarteten) m-dimensionalen Flächen deren heuristischen Flächeninhalt ergeben. (Zu den „anständigen“ Flächen gehören insbesondere die Untermannigfaltigkeiten des
definiert sind und auf den „anständigen“ (nicht entarteten) m-dimensionalen Flächen deren heuristischen Flächeninhalt ergeben. (Zu den „anständigen“ Flächen gehören insbesondere die Untermannigfaltigkeiten des  .)
.)Das bekannteste dieser Maße ist das m-dimensionale Hausdorff-Maß
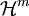 , benannt nach Felix Hausdorff; zur Veranschaulichung der Definition soll zunächst jedoch das m-dimensionale sphärische Maß
, benannt nach Felix Hausdorff; zur Veranschaulichung der Definition soll zunächst jedoch das m-dimensionale sphärische Maß 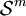 erläutert werden.
erläutert werden.Inhaltsverzeichnis
Definition des sphärischen Maßes
Zu einer Teilmenge A des
 betrachtet man die Größen
betrachtet man die Größenfür ε > 0, wobei das Infimum erstreckt wird über alle Überdeckungen
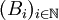 von A durch abzählbar viele m-dimensionale Kugeln B1,B2,... im
von A durch abzählbar viele m-dimensionale Kugeln B1,B2,... im  mit Durchmessern (Diametern) diam(Bi) < ε. Hierbei ist α(m) das Volumen der m-dimensionalen Einheitskugel (Kugel mit Radius 1) im
mit Durchmessern (Diametern) diam(Bi) < ε. Hierbei ist α(m) das Volumen der m-dimensionalen Einheitskugel (Kugel mit Radius 1) im 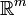 , gleichbedeutend mit dem m-dimensionalen Flächeninhalt des m-dimensionalen Einheitskreises im
, gleichbedeutend mit dem m-dimensionalen Flächeninhalt des m-dimensionalen Einheitskreises im  . Der Formfaktor α(m) sorgt für die richtige „Normierung“ des resultierenden Flächenmaßes. Die Summanden α(m)(diam(Bi) / 2)m sind gerade die m-dimensionalen Flächeninhalte der Schnittmengen der Kugeln Bi mit durch deren Mittelpunkt verlaufenden m-dimensionalen Ebenen im
. Der Formfaktor α(m) sorgt für die richtige „Normierung“ des resultierenden Flächenmaßes. Die Summanden α(m)(diam(Bi) / 2)m sind gerade die m-dimensionalen Flächeninhalte der Schnittmengen der Kugeln Bi mit durch deren Mittelpunkt verlaufenden m-dimensionalen Ebenen im  .
.Das m-dimensionale sphärische Maß von A wird dann, vermöge zunehmender Kleinheit der Kugeln, definiert durch
Die Verfeinerung der Kugelüberdeckungen durch gegen 0 gehende Durchmesser bewirkt eine zunehmende Annäherung der m-dimensionalen Äquatorialflächen der Kugeln an die Ausgangsfläche A.
Definition des Hausdorff-Maßes
Zur Definition des Hausdorff-Maßes
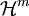 gelangt man, wenn statt der Kugeln alle Teilmengen des
gelangt man, wenn statt der Kugeln alle Teilmengen des  bei den Überdeckungen zugelassen werden. Der Durchmesser von
bei den Überdeckungen zugelassen werden. Der Durchmesser von 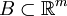 ist definiert durch
ist definiert durchfür
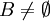 und
und 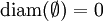 , und man setzt entsprechend
, und man setzt entsprechendwobei hier das Infimum gebildet wird über alle Überdeckungen
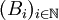 von A durch abzählbar viele (beliebige) Teilmengen B1,B2,... des
von A durch abzählbar viele (beliebige) Teilmengen B1,B2,... des  mit diam(Bi) < ε. Schließlich definiert man
mit diam(Bi) < ε. Schließlich definiert manDie Ausdrücke
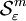 und
und 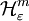 sind selbst äußere Maße und haben durchaus bei gewissen Mengen verschiedene Werte - der Unterschied verschwindet in einigen „pathologischen“ Fällen auch nicht beim Grenzübergang ε gegen 0 - jedoch liefern die beiden Maße
sind selbst äußere Maße und haben durchaus bei gewissen Mengen verschiedene Werte - der Unterschied verschwindet in einigen „pathologischen“ Fällen auch nicht beim Grenzübergang ε gegen 0 - jedoch liefern die beiden Maße 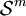 und
und 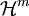 bei den rektifizierbaren (den „anständigen“) m-dimensionalen Mengen denselben Wert. Allgemein gilt die Ungleichung
bei den rektifizierbaren (den „anständigen“) m-dimensionalen Mengen denselben Wert. Allgemein gilt die UngleichungZusammenhang mit der Flächenformel
Zur expliziten Berechnung des Hausdorff-Maßes einer parametrisierten Fläche A = f(G) mit einem Gebiet
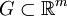 und einer injektiven differenzierbaren Funktion
und einer injektiven differenzierbaren Funktion 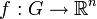 findet die Flächenformel Anwendung:
findet die Flächenformel Anwendung:Dabei ist
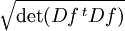 die verallgemeinerte Jacobi-Determinante von f, und
die verallgemeinerte Jacobi-Determinante von f, und 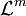 bezeichnet das m-dimensionale Lebesgue-Maß (Volumenmaß) im
bezeichnet das m-dimensionale Lebesgue-Maß (Volumenmaß) im 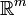 .
.Verallgemeinerungen
(1) Analog verwendet man für „nicht-ganzzahlige Dimensionen“ m die obigen Definitionen von
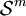 und
und 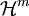 , hier α(m) = Γ(1 / 2)m / Γ(1 + m / 2) mit der Gamma-Funktion Γ für irrationales m. Die Hausdorff-Dimension einer Teilmenge A des
, hier α(m) = Γ(1 / 2)m / Γ(1 + m / 2) mit der Gamma-Funktion Γ für irrationales m. Die Hausdorff-Dimension einer Teilmenge A des  ist dann diejenige (eindeutig bestimmte) Zahl m mit
ist dann diejenige (eindeutig bestimmte) Zahl m mit 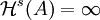 für alle s < m und
für alle s < m und 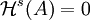 für alle s > m. Wegen der oben genannten Ungleichung spielt der Unterschied zwischen
für alle s > m. Wegen der oben genannten Ungleichung spielt der Unterschied zwischen 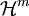 und
und 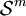 bei der Bestimmung der Hausdorff-Dimension keine Rolle.
bei der Bestimmung der Hausdorff-Dimension keine Rolle.In den letzten Dekaden kamen Fraktale in den Blickpunkt von populärwissenschaftlichen Medien. Fraktale sind Teilmengen des
 mit gebrochener („fraktaler“) Hausdorff-Dimension; in der Öffentlichkeit werden Fraktale überwiegend als Mengen wahrgenommen, die sich neben ihrer fraktalen Dimension noch durch gewisse Selbstähnlichkeiten auszeichnen.
mit gebrochener („fraktaler“) Hausdorff-Dimension; in der Öffentlichkeit werden Fraktale überwiegend als Mengen wahrgenommen, die sich neben ihrer fraktalen Dimension noch durch gewisse Selbstähnlichkeiten auszeichnen.(2) Die Definition des m-dimensionalen Hausdorff-Maßes bleibt ohne wesentliche Veränderungen gültig in jedem metrischen Raum anstelle des
 ; das gleiche gilt für das m-dimensionale sphärische Maß. (Es wird nur die Betragsfunktion in der Definition des Diameters durch die zugrundeliegende Metrik d ersetzt, genauer: aus | x − y | wird d(x,y).)
; das gleiche gilt für das m-dimensionale sphärische Maß. (Es wird nur die Betragsfunktion in der Definition des Diameters durch die zugrundeliegende Metrik d ersetzt, genauer: aus | x − y | wird d(x,y).)Literatur
- Herbert Federer: Geometric Measure Theory. Grundlehren der mathematischen Wissenschaften, Vol. 153, Springer-Verlag Berlin Heidelberg New York, 1969
Wikimedia Foundation.

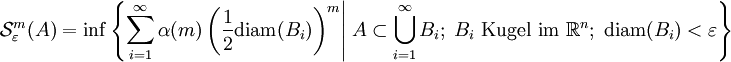
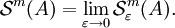
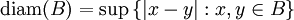
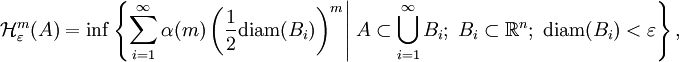
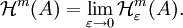
![\mathcal H^m\le \mathcal S^m\le[2n/(n+1)]^{m/2}\mathcal H^m.](/pictures/dewiki/57/904e30f82705be25131d9392b481a935.png)