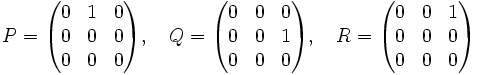Heisenbergalgebra

Die Heisenberg-Algebra ist eine 3-dimensionale, reelle Lie-Algebra mit den Generatoren P, Q, R, für die gilt

[P,Q] = R

[P,R] = [Q,R] = 0

Sie ist die Lie-Algebra der Heisenberggruppe.

Darstellung

Man kann die Heisenberg-Algebra als Algebra von Matrizen darstellen, indem man definiert

$P = \begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}, \quad Q = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{pmatrix}, \quad R = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix}$

und als Lie-Klammer den Kommutator von Matrizen [X,Y] = XY − YX verwendet.

Verallgemeinerung

Entsprechend den verallgemeinerten Heisenberggruppen gibt es auch verallgemeinerte Heisenbergalgebren, die Lie-Algebren der verallgemeinerten Heisenberggruppen.