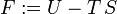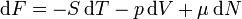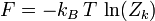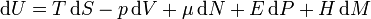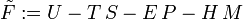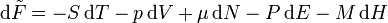Helmholtz-Funktion

Die Freie Energie F (auch Helmholtz-Potential, Helmholtzsche freie Energie oder Helmholtz-Energie nach dem Physiker Hermann von Helmholtz) ist die Energie, die man benötigt, um ein System zu generieren, das bei definierter Temperatur T im thermischen Gleichgewicht mit seiner Umgebung steht. Die freie Energie F = F(T,V,N) ist ein thermodynamisches Potential, das von den natürlichen Variablen Temperatur T, Volumen V und Teilchenzahl N abhängig ist.

Die für Chemie zuständige IUPAC sieht die Bezeichnung Helmholtz-Energie vor mit dem Formelzeichen A, obwohl A bereits für den mathematischen Flächeninhalt reserviert ist und auch gelegentlich für die Energie (Arbeit) benutzt wird. In der Physik hingegen bleiben nach Empfehlung der IUPAP der Begriff Freie Energie und das Formelzeichen F weiterhin gültig.

Thermodynamische Beziehungen

Die freie Energie hängt mit der inneren Energie U zusammen über:

$F:=U-T\, S$

hierbei ist S die Entropie und T die absolute Temperatur des Systems. Im Folgenden werden auch Druck, p, und chemisches Potential, μ, benutzt:

$\mathrm{d}F=-S\,\mathrm{d}T-p\,\mathrm{d}V+\mu\,\mathrm{d}N$

ist die differentielle Form (charakteristische Funktion) für die Helmholtz-Energie, das heißt, dass in einem Versuch Temperatur, Volumen und Teilchenzahl die zu kontrollierenden natürlichen Variablen sind, um F zu ändern (dagegen besitzt die Innere Energie die natürlichen Variablen S, V und N). Isotherme Differenzen der Arbeit (d.h. bei konstanter Temperatur), 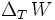$\Delta_T \,W$, lassen sich unter Berücksichtigung des ersten und zweiten Hauptsatzes der Thermodynamik nur im Spezialfall 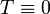$T\equiv 0$ als solche der Inneren Energie oder der Enthalpie berechnen, für T > 0 dagegen nur mit der Helmholtz-Energie. Präzise gilt: Die Änderung der Freien Energie entspricht bei isothermen Prozessen der maximalen Arbeit, die ein System verrichten kann.

Die freie Energie ist das zum kanonischen Ensemble gehörende thermodynamische Potential und ist über folgende Beziehung mit der kanonischen Zustandssumme Z_k verknüpft:

$F=-k_{B}\,T\,\ln(Z_{k})$

Bei kanonischer Präparierung eines Systems (abgeschlossenes System V=const, N=const im Wärmebad T = T₀) wird im thermodynamischen Gleichgewicht die freie Energie minimal.

Thermodynamik mit elektromagnetischen Feldern

Unter Einbeziehung elektrischer und magnetischer Felder ist die innere Energie gegeben durch:

$\mathrm{d}U=T\,\mathrm{d}S-p\,\mathrm{d}V+\mu\,\mathrm{d}N+E\,\mathrm{d}P+H\,\mathrm{d}M$

Dabei ist ist E die elektrische Feldstärke, H die magnetische Feldstärke, P die Polarisation mal Volumen, M die Magnetisierung mal Volumen. Die freie Energie wird nun definiert über:

$\tilde{F}:=U-T\, S-E\, P-H\, M$

mit den natürlichen Variablen Temperatur T, Volumen V und Teilchenzahl N, elektrisches Feld E und Magnetfeld H. Das totale Differential lautet:

$\mathrm{d}\tilde{F}=-S\,\mathrm{d}T-p\,\mathrm{d}V+\mu\,\mathrm{d}N-P\,\mathrm{d}E-M\,\mathrm{d}H$

Für konstante Volumen, Teilchenzahlen und elektrische Felder wird daraus die einfache Form: $\mathrm{d}\tilde{F}=-S\,\mathrm{d}T-M\,\mathrm{d}H$

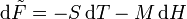
Literatur

• Callen: Thermodynamics and an Introduction to Thermostatistics. Wiley & Sons. ISBN 978-0471862567
• Schwabl: Statistische Mechanik. Springer. ISBN 978-3540310952