Helmholtz-Konfiguration

Helmholtz-Spulen

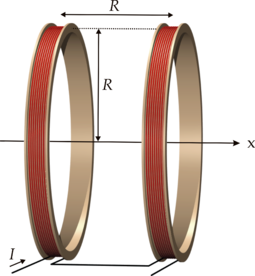
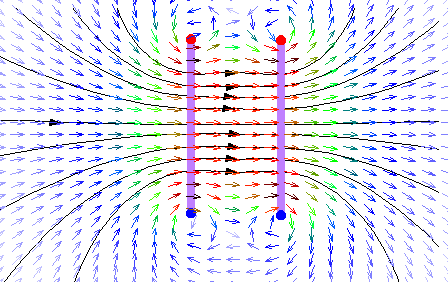
Als Helmholtz-Spule bezeichnet man eine besondere Spulenanordnung, die auf den deutschen Physiker Hermann von Helmholtz (1821–1894) zurückgeht: Zwei kurze Spulen mit großem Radius R werden im Abstand R auf gleicher Achse parallel aufgestellt. Das Feld jeder einzelnen Spule ist inhomogen. Durch die Überlagerung beider Felder ergibt sich zwischen beiden Spulen nahe der Spulenachse ein Bereich mit weitgehend homogenem Magnetfeld, das für Experimente frei zugänglich ist. Es gibt Helmholtzspulen in verschiedenen Bauformen: zylindrisch, quadratisch, aber auch dreidimensional. Mit der dreidimensionalen Spule kann man ein Magnetfeld beliebiger Richtung erzeugen und damit einen Gegenstand untersuchen, ohne diesen drehen zu müssen.

Anwendungen der Helmholtzspule

Helmholtzspule mit Fadenstrahlrohr

• Bestimmung der spez. Elektronenladung nach Helmholtz mit Fadenstrahlrohr
• Qualitätskontrolle von Hartmagneten
• Hall-Effektuntersuchungen
• Kalibrierung von Magnetfeldsonden
• HF-Spule bei der Magnetresonanztomographie
• Gradientenspule (als Maxwellspule) in Magnetresonanztomographie
• Magnetfeldtherapie
  Die therapeutische Wirkung von Magnetfeldern ist umstritten. Neben esoterischen Behauptungen gibt es auch einige wissenschaftliche Hypothesen, nach denen durch Induktion Veränderungen chemischer und physikalischer Vorgänge in den Zellmembranen ausgelöst werden könnten. Konkrete Nachweise bei lebenden Zellen fehlen.

Vorteile

Die erzeugte magnetische Feldstärke steht in einem streng linearen Zusammenhang zum Spulenstrom. Aus der Spulengeometrie, dem Strom und der Windungszahl lässt sich die resultierende Feldstärke exakt analytisch (oder auch numerisch) berechnen. Daher ist die Helmholtzspule ideal für die Kalibrierung von Magnetometern, wie etwa Fluxgate-Magnetometern, einsetzbar.

Berechnung der magnetischen Flussdichte

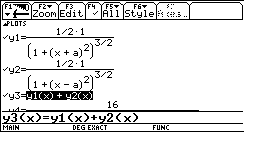
Wenn der Ursprung des Koordinatensystems im Zentrum der Spule liegt, ergibt sich mit dem Biot-Savart-Gesetz für die magnetische Flussdichte im Vakuum entlang der Symmetrieachse:

$\vec{B}(x)=\frac{\mu_0 I}{2}\cdot\frac{R^2}{\left(R^2+x^2\right)^{\frac{3}{2}}}\,\vec{e}_x$

Feldverlauf einer kurzen Spule

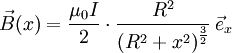
Die Flussdichte im Zentrum des Helmholtz-Spulenpaars ist die Überlagerung zweier Kreisströme im Abstand $\pm R/2$:

$B\left(\frac{R}{2}\right)=\frac{1}{2} \cdot\mu_0\cdot\frac{I\cdot R^2}{\left(R^2+\left(\frac{R}{2}\right)^2\right)^{\frac{3}{2}}}$

$\begin{align} B\left(\frac{R}{2}\right) + B\left(\frac{-R}{2}\right) &= \frac12 \cdot\mu_0\cdot\frac{I\cdot R^2}{\left(R^2+\left(\frac{R}{2}\right)^2\right)^{\frac32}} \\&\quad + \frac12 \cdot\mu_0\cdot\frac{I\cdot R^2}{\left(R^2+\left(\frac{-R}{2}\right)^2\right)^{\frac32}} \\&=2\cdot B\left(\frac{R}{2}\right) \;=\; \mu_0\cdot\frac{I\cdot R^2}{\left(R^2+\frac{R^2}{4}\right)^{\frac32}} \\&= \mu_0\cdot\frac{8\cdot I}{\sqrt{125}\cdot R} \end{align}$

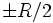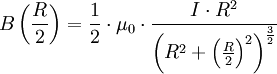
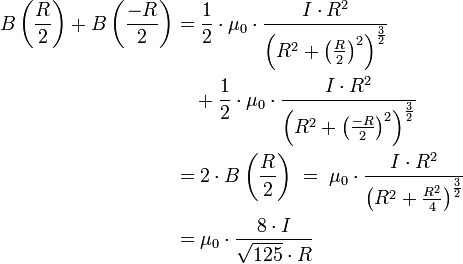
wobei μ₀ die magnetische Leitfähigkeit des leeren Raumes ist, I die Spulenstromstärke und R der Spulenradius.

Helmholtzspulenpaar mit je N Windungen

Ursprung des Koordinatensystems in der Mitte zwischen den Spulen.

$\begin{align} B(0) &= \mu_0\cdot \frac{8\cdot I\cdot N}{\sqrt{125}\cdot R} \\ &= 4\cdot\pi \cdot 10^{-7}\frac{\mathrm V\cdot \mathrm s}{\mathrm A\cdot\mathrm m}\cdot 0{,}716\cdot\frac{I\cdot N}{R} \end{align}$

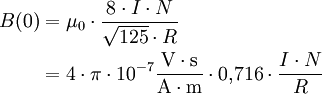
Beispiel: I = 1,7 A; N = 130; R = 0,15 m

$B(0)=4\cdot\pi \cdot 10^{-7}\frac{\mathrm V\cdot \mathrm s}{\mathrm A\cdot\mathrm m}\cdot 0{,}716\cdot\frac{1{,}7\,\mathrm A\cdot 130}{0,15\,\mathrm m}= 1{,}33\cdot10^{-3}\;\mathrm T$

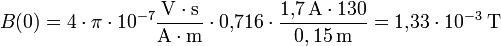
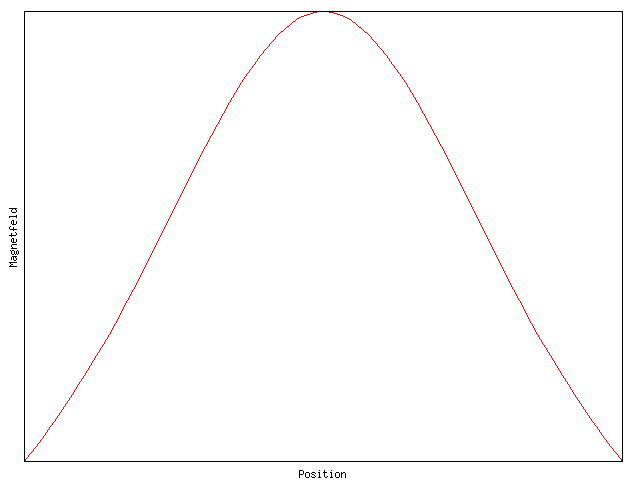
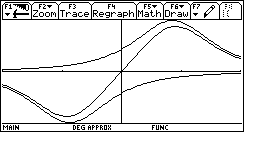
Feldverläufe bei verschiedenen Spulenabständen

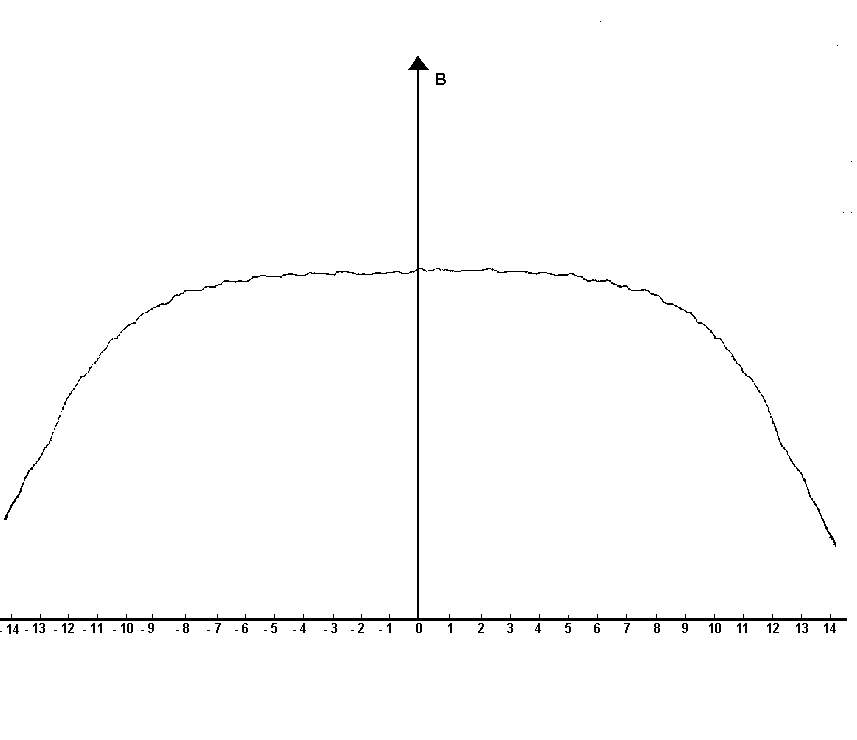
Bei der Anordnung nach Helmholtz verschwindet in der Mitte die erste und die zweite Ableitung der Feldfunktion, nach den Seiten fällt die Feldstärke relativ schnell ab. Das ist in der untenstehenden Bildergalerie ersichtlich.

Größere Abstände ergeben ein größeres Experimentiervolumen, aber zur Spulenmitte hin abfallende Feldstärkewerte. Kleinere Abstände ergeben größere Feldstärken, aber ein kleineres Experimentiervolumen und die gemessenen Werte ergeben eine gute Übereinstimmung mit den gerechneten Werten. Mit Eisenfeilspänen kann im Experiment die gute Homogenität des Magnetfeldes in der Nähe der Spulenachse gezeigt werden.

Maxwellspule

Durchfließt der Strom die Spulen gegensinnig, so wird bei geeignet gewählter Geometrie im Inneren ein konstanter Feldgradient erzeugt. Ist der Abstand der Spulen zueinander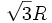$\sqrt{3} R$, dann verschwindet bei x=0 die zweite und die dritte Ableitung, die Feldfunktion ist dort also eine Gerade. Man nennt die Spulenanordnung dann Maxwell-Spule, manchmal auch Anti-Helmholtz-Spule.

Bildgalerie

Nachfolgend sind gemessene oder errechnete Feldverläufe bei Helmholzspulen dargestellt:

Verteilungsfunktionen	Abstand zur Mitte a=0,5 R (Anordnung nach Helmholtz)	Abstand zur Mitte a=0,54 R (längste homogene Strecke)	Abstand zur Mitte a=0,55 R (leichte Einsenkung)
Abstand zur Mitte a=0,5985 R (drei gleiche Werte B(-a)=B(0)=B(a))	Feldverlauf in Richtung der Spulenachse (gemessen)	Feldverlauf quer zur Richtung der Spulenachse (gemessen)	Magnetfeld der Helmholtzspule mit Eisenfeilspänen sichtbar gemacht
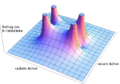
Berechnetes Magnetfeld der Helmholtzspule	Feldverlauf bei optimierten Spulenabstand von a=sqrt(3)/2	B-Feldstärke entlang der Achse durch das Zentrum der Spulen; z=0 ist der Punkt in der Mitte zwischen den Spulen.	Betrag der B-Feldstärke als Funktion des Ortes. Die Schnittebene geht durch das Zentrum.