Hitting set

Dieser Artikel oder Abschnitt ist nicht hinreichend mit Belegen (Literatur, Webseiten oder Einzelnachweisen) versehen. Die fraglichen Angaben werden daher möglicherweise demnächst gelöscht. Hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Bitte entferne erst danach diese Warnmarkierung.

Das Hitting-Set-Problem ist ein NP-vollständiges Problem aus der Mengentheorie.

Es gehört zur Liste der 21 klassischen NP-vollständigen Probleme von denen Richard Karp 1972 die Zugehörigkeit zu dieser Klasse zeigen konnte.

Gegeben ist eine Menge von Teilmengen S eines "Universums" T, gesucht ist eine Teilmenge H von T so, dass jede Menge in S mindestens ein Element aus H enthält. Zusätzlich ist gefordert, dass die Zahl der Elemente von H einen gegebenen Wert K nicht überschreitet.

Formale Definition

Gegeben:

• eine Kollektion von Mengen {S₁,S₂,...,S_n}, wobei jedes S_i eine Teilmenge von T ist und
• eine positive ganze Zahl $K \le |T|$

Die Aufgabe besteht darin, festzustellen, ob eine Teilmenge H von T existiert, sodass

$|H| \le K \and \forall i \in \{1,2,...,n\}: (H \cap S_i) \ne \emptyset$.

NP-Vollständigkeit

Es kann gezeigt werden, dass das Hitting Set Problem NP-vollständig ist, indem es auf das Knotenüberdeckungsproblem zurückgeführt wird.

Beweis

Es sei <G, k> eine Instanz des Knotenüberdeckungsproblems (Vertex Cover Problem) und G = (V, E). Es sei T = V und 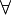$\forall$ (u, v) 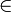$\in$ E wird eine neue Menge {u,v} der Kollektion hinzugefügt. Dann zeigen wir, dass es ein Hitting Set H der Größe k genau dann gibt, wenn G eine Knotenüberdeckung C der Größe k hat.

($\Rightarrow$) Angenommen, es gibt ein Hitting Set H der Größe k. Da H mindestens einen Endpunkt jeder Kante enthält, ergibt sich mit C := H eine Knotenüberdeckung der Größe k.

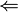($\Leftarrow$) Angenommen, es gibt eine Knotenüberdeckung C für G der Größe k. Für jede Kante (u,v) ist entweder u 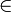$\in$ C oder v 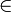$\in$ C. Mit C := H ergibt sich ein Hitting Set der Größe k.