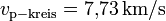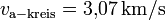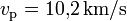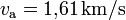Hohmann-Transfer

Unter der Hohmannbahn oder Hohmann-Ellipse versteht man in der Raumfahrt die energetisch günstigste Bahn, um von einer kreisförmigen Umlaufbahn in eine andere zu wechseln, bzw. von einem Planeten zu einem anderen zu gelangen. Gleichzeitig verlängert sich aber die Reisezeit um ein Vielfaches. Die Übergangsbahn ist eine Ellipse, die sowohl den Anfangspunkt, als auch den Endpunkt tangential berührt.

Der Name geht zurück auf den deutschen Ingenieur Walter Hohmann und seine Schrift Die Erreichbarkeit der Himmelskörper (1925).

Das sogenannte Weak Stability Boundary-Verfahren optimiert zusätzlich die Abbremsung.

Beispiel

Transferbahn zum Mars

Transfer Erde->Mars

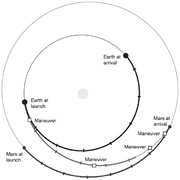Transferbahn einer Mars-Sonde.

Der Mars ist der Erde in Oppositionsstellung am nächsten. Ein Satellit kann die geometrische Nähe nur unter hohem Aufwand nutzen, da er gegen die Bahnbewegung der Erde anfliegen muss.

Nach Hohmann ist der energetisch günstigste Transfer der, wenn der Satellit den Mars in Konjunktion zur Position der Erde erreicht, die die Erde bei seinem Abflug inne hatte. In der Abbildung links startet die Sonde auf der Erde bei (1) und erreicht den Mars bei Position (3). Die Sonne steht dabei in einem der Brennpunkte der Transferbahn (gelb). Die doppelte Halbachse der Transferellipse ist die Summe aus der Entfernung Erde-Sonne und Sonne-Mars. Daraus ergibt sich nach dem dritten Keplerschen Gesetz eine halbe Umlaufzeit von knapp einem Jahr.

Das Bild rechts zeigt die Transferbahn des Mars Reconnaissance Orbiters. Sie erfordert einen höheren Energieaufwand als die Hohmann-Bahn, dafür ist die Sonde nur 7 Monate zum Mars unterwegs.

Transfer auf geostationäre Bahn

Hohmannübergang von (1) nach (3).

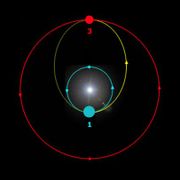
Um Satelliten in eine geostationäre Bahn (GEO, Geostationary Earth Orbit) zu positionieren, werden sie zunächst auf eine niedrige kreisförmige Umlaufbahn (LEO, Low Earth Orbit) gebracht, siehe (1) in der Zeichnung. Dort erfolgen zwei Bahnkorrekturen. Die erste weitet die Kreisbahn auf in eine Ellipse (Geostationäre Transferbahn) mit dem Apogäum beim zu erreichenden GEO, siehe (2). Die zweite Korrektur erfolgt im Apogäum und bringt den Satelliten auf den gewünschten kreisförmigen GEO, siehe (3). Vereinfachend wird angenommen, dass eine kurzzeitige Zündung des Triebwerks für die Geschwindigkeitsänderung genügt. In Wirklichkeit wird sich der notwendige Schub nur über eine längere Brenndauer erreichen lassen, wodurch weitere Bahnkorrekturen erforderlich werden.

Einige Trägerraketen wie die Ariane-Raketen setzen jedoch die Satelliten gleich in der Geostationären Transferbahn aus, so das der Satellit nur noch das als Ziffer (3.) bezeichnete Schubmanöver durchführen muss.

Nach den Keplerschen Gesetzen beträgt die Geschwindigkeit v(r) eines Körpers am Ort r auf einer Ellipsenbahn mit der großen Halbachse a um die Erde:

(1) $v = \sqrt{\mu \cdot \left(\frac{2}{r} - \frac{1}{a} \right) }$

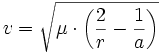
mit 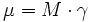$\mu = M \cdot \gamma$, wobei M die Erdmasse und γ die Gravitationskonstante sind.

Bezeichnen r_p den Perigäum-Radius, r_a den Apogäum-Radius und 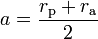$a = \frac{r_\mathrm{p} + r_\mathrm{a}}{2}$ die große Halbachse der Transferellipse, so gilt für die Perigäums- und Apogäumsgeschwindigkeit:

(2) $v_\mathrm{p} = \sqrt{\frac{\mu}{a} \cdot \frac{r_\mathrm{a}}{r_\mathrm{p}} }$

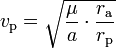
(3) $v_\mathrm{a} = \sqrt{\frac{\mu}{a} \cdot \frac{r_\mathrm{p}}{r_\mathrm{a}} }$

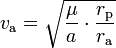
und für die entsprechenden Kreisbahn-Geschwindigkeiten v(r_p)_p bzw v(r_a)_a:

(4) $v(r) = \sqrt{ \frac{\mu}{r} }$

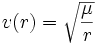
Zahlenbeispiel

Folgende Werte seien gegeben:

$\mu = 398'600\, \mathrm{km}^3/\mathrm{s}^2$

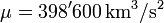
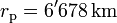$r_\mathrm{p} = 6'678\, \mathrm{km}$ (gemessen vom Erdmittelpunkt bei einer Flughöhe von 300 km)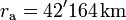

$r_\mathrm{a} = 42'164\, \mathrm{km}$

Dann betragen die Kreis-Umlaufgeschwindigkeiten:

(5) $v_\mathrm{p-kreis} = 7{,}73\, \mathrm{km}/\mathrm{s}$ [1]

(6) $v_\mathrm{a-kreis} = 3{,}07\, \mathrm{km}/\mathrm{s}$ [2]

Und die Geschwindigkeiten im Perigäum bzw. Apogäum:

(7) $v_\mathrm{p} = 10{,}2\, \mathrm{km}/\mathrm{s}$ [3]

(8) $v_\mathrm{a} = 1{,}61\, \mathrm{km}/\mathrm{s}$ [4]

Daraus ergeben sich die beiden Geschwindigkeitsänderungen.

Für die Änderung von der Kreisbahn auf die elliptische Bahn: (7)-(5) = 2,4 km/s

Für die Änderung von der Ellipse auf den GEO: (6)-(8) = 1,46 km/s

Weak Stability Boundary

Die Hohmannbahn ist die energetisch günstigste Transferbahn von einem Planeten zu einem anderen. Soll der Zielplanet mit einer möglichst geringen Geschwindigkeit angeflogen werden, bietet das sogenannte Weak Stability Boundary-Verfahren einen weiteren Energiegewinn. Die Sonde wird abgebremst, indem sie entlang von Librationspunkten manövriert wird. Eine erste brauchbare Bahnberechnung erfolgte 1986. Die ESA-Sonde Smart-1 näherte sich nach dieser Methode dem Mond.

Siehe auch

• Swing-by
• Hillsche Gleichungen
• Geostationäre Transferbahn

Weblinks

• http://www.urbin.de/next_step/next_step.htm (Das Problem der idealen Flugbahn)
• http://www.schulphysik.de/java/physlet/applets/hohmann1.html (Hohmann Bahn - von Planet zu Planet) - mit Java Applet
• Assessment of Mission Design Including Utilization of Libration Points and Weak Stability Boundaries