Hornformel

Horn-Formeln sind eine spezielle Teilmenge der aussagenlogischen Formeln. Benannt wurden sie nach dem US-amerikanischen Logiker Alfred Horn.

Definition mit Horn-Klauseln

Eine Horn-Klausel ist eine Klausel mit höchstens einem positiven Literal, d.h. höchstens einem Literal, in dem die Variable nicht negiert vorkommt. Eine Horn-Formel ist eine Konjunktive Normalform (das heißt eine Konjunktion von Disjunktionen), bei der jeder Disjunktionsterm eine Horn-Klausel ist, also eine Disjunktion von Literalen, von denen höchstens eines unverneint (positiv) auftritt.

Beispiele

• $(\neg P \vee \neg Q \vee R) \wedge (P \vee \neg Q \vee \neg S) \wedge (\neg R \vee \neg S)$

(die dritte Horn-Klausel hat kein, die beiden anderen Horn-Klauseln haben je ein positives Literal)

• $(x_1 \vee \neg x_2 \vee \neg x_3) \wedge (\neg x_1 \vee \neg x_2 \vee \neg x_3 \vee x_4)$

Darstellungsformen von Horn-Klauseln

Horn-Klauseln lassen sich nach den Regeln der Aussagenlogik auch als materiale Implikationen darstellen. Die folgende Tabelle gibt einen Überblick über die zwei möglichen Typen einer Horn-Klausel und ihre Form sowohl als Disjunktion als auch als Implikation.

Name	Beschreibung	Disjunktion	Implikation	In Worten
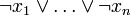
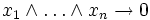
Zielklausel	Kein positives Literal	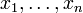$\neg x_1 \vee \ldots \vee \neg x_n$	$x_1 \wedge \ldots \wedge x_n \rightarrow 0$	$x_1, \ldots, x_n$ sind nicht alle wahr
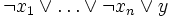
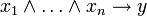
definite Hornklausel	Genau ein positives Literal	$\neg x_1 \vee \ldots \vee \neg x_n \vee y$	$x_1 \wedge \ldots \wedge x_n \rightarrow y$	Wenn 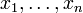$x_1, \ldots, x_n$ wahr sind, dann ist auch y wahr

Die Anzahl der negativen Literale (n) kann für Klauseln mit genau einem positiven Literal auch 0 sein (teilweise lässt man auch die leere Klausel als Zielklausel zu).

Erfüllbarkeit

Mit Hilfe des Markierungsalgorithmus können Horn-Formeln in Polynomialzeit auf Erfüllbarkeit getestet werden (folglich ist HORNSAT P-vollständig). Man kann also in Polynomialzeit feststellen, ob eine Variablenbelegung (eine Zuordnung von Wahrheitswerten zu den in in der Horn-Formel vorkommenden Literalen) existiert, für die die Horn-Formel wahr wird. Im Unterschied dazu wird vermutet, dass allgemein für aussagenlogische Formeln kein Polynomialzeit-Algorithmus existiert (siehe Erfüllbarkeitsproblem der Aussagenlogik).

Anwendung

Die Bedeutung der Horn-Klauseln liegt zum Beispiel in der Informatik beim maschinellen Schließen. So werden in der Programmiersprache Prolog Programme als Horn-Klauseln angegeben.

Siehe auch

• Gentzenscher Hauptsatz
• Sequenzenkalkül