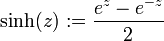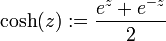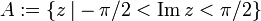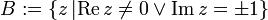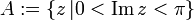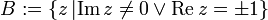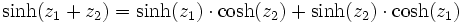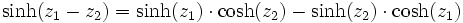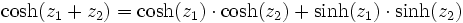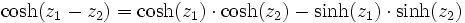- Hyperbelfunktionen
-
Zu den Hyperbelfunktionen gehören:
- Sinus Hyperbolicus
- Kosinus Hyperbolicus
- Tangens Hyperbolicus
- Kotangens Hyperbolicus
- Sekans Hyperbolicus
- Kosekans Hyperbolicus,
abgekürzt durch sinh, cosh, tanh, coth, sech und csch.
sinh und cosh sind für alle komplexen Zahlen definiert und auf dem gesamten Gebiet der komplexen Zahlen holomorph. Die übrigen Hyperbelfunktionen haben Pole auf der imaginären Achse.
Inhaltsverzeichnis
Definition
Definition über die Exponentialfunktion
Daher sind die hyperbolischen Funktionen periodisch (mit rein imaginärer Periode). Die Potenzreihen von cosh(z) und sinh(z) entstehen aus denen von cos(z) und sin(z), indem alle Minuszeichen durch Pluszeichen ersetzt werden.
Geometrische Definition mit Hilfe der Hyperbel
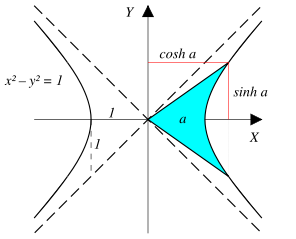
Der Name Hyperbelfunktionen stammt daher, dass die Funktionen eine Hyperbel x2 − y2 = 1 beschreiben, nämlich mit Hilfe der Parameterdarstellung
x = cosh(t), y = sinh(t).
(Vergleiche den Zusammenhang zwischen dem Einheitskreis x2 + y2 = 1 und seiner Parameterdarstellung x = cos(t) und y = sin(t).)
Die Funktionen stellen eine Verbindung her zwischen der Fläche a, die von einer vom Nullpunkt ausgehenden Geraden und ihrem Spiegelbild an der x-Achse sowie der Hyperbel eingeschlossen wird, und der Länge verschiedener Strecken.
Dabei ist sinh(a) die (positive) y-Koordinate des Schnittpunkts der Geraden mit der Hyperbel und cosh(a) die dazugehörige x-Koordinate. tanh(a) ist die y-Koordinate der Geraden bei x=1, d.h. die Steigung der Geraden.
Berechnet man die Fläche durch Integration, erhält man die Darstellung mit Hilfe der Exponentialfunktion.
Wertebereich der reellen Hyperbelfunktionen
Für alle reelle Zahlen r sind auch sinh(r) und cosh(r) reell.
Die reelle Funktion sinh ist streng monoton steigend und besitzt in 0 ihren einzigen Wendepunkt.
Die reelle Funktion cosh ist für Werte < 0 streng monoton fallend,
für Werte > 0 streng monoton steigend.
Wertebereich der komplexen Hyperbelfunktionen
sinh
Es seien folgende Teilmengen der komplexen Zahlen definiert:
Dann bildet die komplexe Funktion sinh den „Streifen“ A bijektiv auf B ab.
cosh
Es seien folgende Teilmengen der komplexen Zahlen definiert:
Dann bildet die komplexe Funktion cosh den „Streifen“ A bijektiv auf B ab.
Eigenschaften der komplexen Hyperbelfunktionen
Symmetrie und Periodizität
Für alle komplexen Zahlen z gilt:
- sinh(z) = − sinh( − z), d.h. sinh ist eine ungerade Funktion.
- cosh(z) = cosh( − z), d.h. cosh ist eine gerade Funktion.
Es liegt rein imaginäre Periodizität vor.
Additionstheoreme
Für alle komplexen Zahlen z1 und z2 gilt:
Zusammenhänge
- cosh2(z) − sinh2(z) = 1
Ableitung
Die Ableitung des Sinus Hyperbolicus lautet:
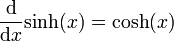 .
.
Die Ableitung des Kosinus Hyperbolicus lautet:
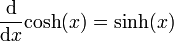 .
.
Die Ableitung der Tangens Hyperbolicus lautet:
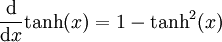 .
.
Alternative Namen
- Für die Hyperbelfunktionen ist auch der Name hyperbolische Funktionen gebräuchlich.
- Für sinh sind auch die Namen hsin, Hyperbelsinus und Sinus hyperbolicus gebräuchlich.
- Für cosh sind auch die Namen hcos, Hyperbelcosinus und Cosinus hyperbolicus gebräuchlich.
Abgeleitete Funktionen
- Tangens Hyperbolicus
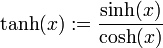
- Cotangens Hyperbolicus
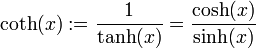
- Secans Hyperbolicus
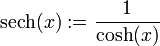
- Cosecans Hyperbolicus
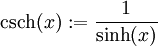
Umrechnungstabelle
Funktion sinh cosh tanh coth sinh(x) = 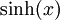
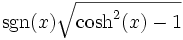
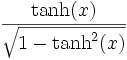
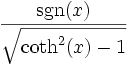
cosh(x) = 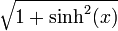
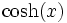
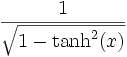
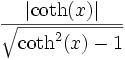
tanh(x) = 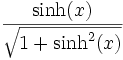
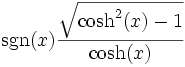
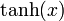
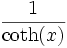
coth(x) = 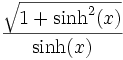
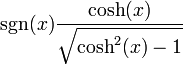
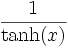
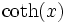
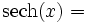
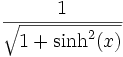
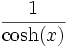
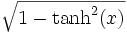
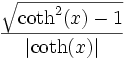
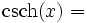
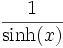
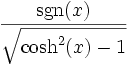
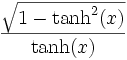
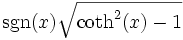
Funktion 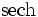
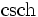
sinh(x) = 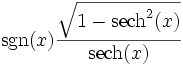
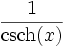
cosh(x) = 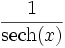
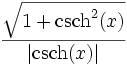
tanh(x) = 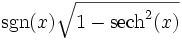
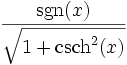
coth(x) = 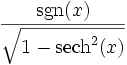
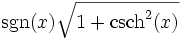
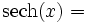
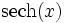
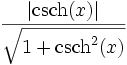
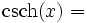
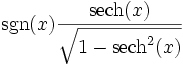
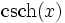
Umkehrfunktionen
Die Umkehrfunktionen der Hyperbelfunktionen heißen Area-Funktionen. Siehe auch: Zusammenhang mit den Kreisfunktionen
Weblinks
Literatur
- Ilja N. Bronstein: Taschenbuch der Mathematik. Deutsch (Harri).
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.