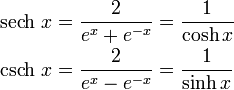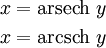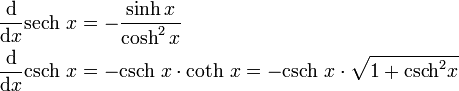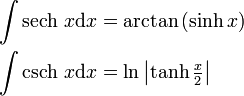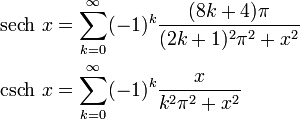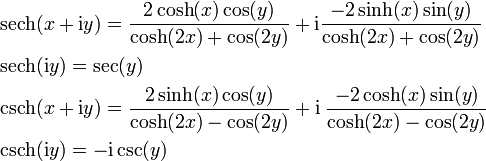- Csch
-
Sekans Hyperbolicus (blau) und Kosekans Hyperbolicus (rot)
Die Funktionen Sekans Hyperbolicus (
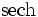 ) und Kosekans Hyperbolicus (
) und Kosekans Hyperbolicus (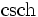 ) sind Hyperbelfunktionen.
) sind Hyperbelfunktionen.Inhaltsverzeichnis
Definitionen
Eigenschaften
Sekans Hyperbolicus Kosekans Hyperbolicus Definitionsbereich 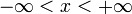
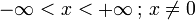
Wertebereich 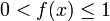
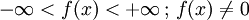
Periodizität keine keine Monotonie x < 0 streng monoton steigend
x > 0 streng monoton fallendx > 0 streng monoton fallend
x < 0 streng monoton fallendSymmetrien Spiegelsymmetrie zur y-Achse Punktsymmetrie zum Koordinatenursprung Asymptote 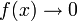 für
für 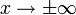
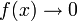 für
für 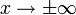
Nullstellen keine keine Sprungstellen keine keine Polstellen keine x = 0 Extrema Maximum bei x = 0 keine Wendepunkte 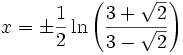
keine Umkehrfunktionen
Die Umkehrfunktion sind die entsprechende Areafunktionen:
Ableitungen
Integrale
Reihenentwicklungen
Komplexes Argument
Siehe auch
Weblinks
- Eric W. Weisstein: Hyperbolic Secant und Hyperbolic Cosecant auf MathWorld
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.