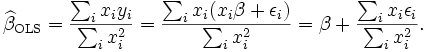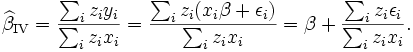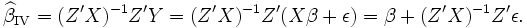Instrumentenvariable

Die Methode der Instrumentenvariablen (IV, Instrument) ist ein Oberbegriff für bestimmte Schätzverfahren in der schließenden Statistik. Sie zählt zur Familie der GMM-Schätzer (en:Generalized method of moments), eine Verallgemeinerung der Momentenmethode, die 1982 von Hansen vorgeschlagen wurde.

Ziel der IV-Methode ist es, bei einer Regressionsanalyse die zwischen dem Fehlerterm und den erklärenden Variablen auftretende Korrelation zumindest asymptotisch zu eliminieren, indem man die erklärenden Variablen durch andere Größen ersetzt, die zwar in engem Zusammenhang mit ihnen stehen, aber nicht mit dem Fehlerterm korrelieren oder eine Linearkombination anderer erklärender Variablen darstellen.

Die Korrelation zwischen dem Fehlerterm und den erklärenden Variablen wird als Endogenität bezeichnet. Diese Endogenität kann aus verschiedenen Kanälen entstehen, Simultanität, Meßfehler oder ausgelassene Variablen. Um ein Modell auf Endogenität zu überprüfen, kann der Hausman-Test angewandt werden.

Die Zahl der möglichen Instrumente ist groß: beispielsweise können exogene Variablen aus Vorperioden oder Differenzen aus diesen herangezogen werden. Je weiter diese aber zeitlich entfernt sind, desto schwächer werden sie vermutlich werden.

Bekannte Beispiele für Instrumentvariablen in Querschnittsdaten sind Charakteristika der Eltern (Bildung der Eltern als Instrument für Bildung der Kinder).

Der IV-Schätzer führt gegenüber dem Kleinste-Quadrate-Schätzer zu höheren Standardfehlern, dies resultiert vor allem aus einer geringen Korrelation von Regressor und IV. Ein weiteres Problem besteht in der Auswahl der passenden Instrumente. Die bezüglich der Momentenbedingungen getroffenen Annahmen können statistisch nur dann getestet werden, wenn mehr Bedingungen als notwendig vorhanden sind, dann aber auch nur ohne Aussage, welche der Momentenbedingungen überflüssig sind.

Mathematischer Hintergrund

Für den Kleinst-Quadrate-Schätzer gilt:

$\widehat{\beta}_\mathrm{OLS} = \frac{\sum_i x_i y_i}{\sum_i x_i^2} = \frac{\sum_i x_i (x_i \beta + \epsilon_i)}{\sum_i x_i^2} = \beta + \frac{\sum_i x_i \epsilon_i}{\sum_i x_i^2}.$

Wenn x und ε nicht korreliert sind, geht der zweite Term bei unendlich vielen Beobachtungen gegen Null und der Schätzer ist konsistent. Wenn x und ε korreliert sind, ist der Schätzer verzerrt.

Eine Instrumentvariable ist mit der erklärenden Variable, aber nicht mit dem Fehlerterm korreliert. Der Schätzer lautet:

$\widehat{\beta}_\mathrm{IV} = \frac{\sum_i z_i y_i}{\sum_i z_i x_i} = \frac{\sum_i z_i (x_i \beta + \epsilon_i)}{\sum_i z_i x_i} = \beta + \frac{\sum_i z_i \epsilon_i}{\sum_i z_i x_i}.$

Wenn z und ε nicht korreliert sind, verschwindet der letzte Term und führt zu einem konsistenten Schätzer. Beachte: Ist x nicht mit dem Fehlerterm korreliert, ist x selbst eine Instrumentenvariable. In diesem Fall ist der KQ-Schätzer mit dem IV-Schätzer identisch.

Der Ansatz oben kann leicht zu einer Regression mit mehreren erklärenden Variablen verallgemeinert werden. X sei eine T x K Matrix von erklärenden Variablen, die aus T Beobachtungen von K Variablen resultiert. Z sei eine T x K Matrix von Instrumentvariablen. Dann folgt

$\widehat{\beta}_\mathrm{IV} = (Z'X)^{-1}Z'Y = (Z'X)^{-1}Z'(X\beta+\epsilon) = \beta + (Z'X)^{-1}Z'\epsilon.$

Diese Technik wird häufig mittels two-stage least-squares (2SLS) implementiert. Im ersten Schritt des 2SLS-Ansatzes wird jede endogene erklärende Variable auf alle gültigen Instrumente sowie alle exogenen Variablen regressiert. Da die Instrumente exogen sind, wird diese Approximation der endogenen Variablen nicht mit dem Fehlerterm korrelieren.

Intuitiv: Es wird die Beziehung zwischen y und den endogenen erklärenden Variablen untersucht. Im zweiten Schritt wird die interessierende Regression wie gewohnt geschätzt, aber alle endogenen erklärenden Variablen werden durch die Näherungswerte aus Schritt 1 ersetzt

Der so gewonnene Schätzer ist konsistent. Damit die Standardfehler richtig berechnet werden, muss nun nur noch die Summe der quadrierten Fehlerterme korrigiert werden

Schritt 1: $\widehat{X}= Z(Z'Z)^{-1}Z'X$

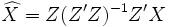
Schritt 2: $\widehat{B}_\mathrm{IV} = (\widehat{X}'\widehat{X})^{-1}\widehat{X}'Y$

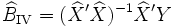
Weiterführende Literatur

• Ahn, Seung C.; Schmidt, Peter (1995): Efficient estimation of models for dynamic panel data. in: Journal of Econometrics, Vol. 68, Iss. 1, 1995, Seite 5-27.
• Eckey, Hans-Friedrich/Kosfeld, Reinhold/Dreger, Christian (2004): Ökonometrie. 3., überarb. und erw. Aufl., Wiesbaden: Gabler, 2004.
• Greene, William H. (2003): Econometric Analysis. 5. Aufl., Upper Saddle River, NJ: Prentice Hall, 2003.
• Verbeek, Marno (2004): A Guide to Modern Econometrics: 2. Aufl., Chichester: John Wiley & Sons, 2004.
• Wooldridge, Jeffrey M. (2002): Econometric Analysis of Cross Section and Panel Data, Cambridge, Mass. [u.a.] : MIT Press, 2002.