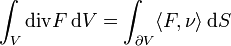- Integralsatz von Stokes
-
Der Satz von Stokes oder Stokes'scher Integralsatz (nach Sir George Gabriel Stokes), häufig auch allgemeiner Satz von Stokes genannt, ist ein Ergebnis aus der Differentialgeometrie. In seiner allgemeinsten Form handelt es sich um einen sehr tiefliegenden Satz über die Integration von Differentialformen, der den Hauptsatz der Differential- und Integralrechnung verallgemeinert. Es geht darum, n-dimensionale Volumenintegrale über das Innere in Randintegrale über die Oberfläche des Volumenstücks umzuwandeln. Häufig werden speziellere Varianten des allgemeinen Satzes angegeben, aus denen das allgemeine Prinzip mehr oder minder gut ersichtlich ist; die beiden wichtigsten Spezialfälle, der gaußsche Integralsatz und der spezielle stokessche Integralsatz (siehe unten) entstammen der Vektoranalysis. In der Physik erlaubt der Satz von Stokes elegante Schreibweisen physikalischer Zusammenhänge, zum Beispiel bei den integrierten Formen der Maxwellschen Gleichungen.
Inhaltsverzeichnis
Klassischer Integralsatz von Stokes
Der klassische Integralsatz von Stokes ist auch als Satz von Kelvin-Stokes oder Rotationssatz bekannt und seine Aussage ist:
Es sei
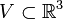 eine offene Teilmenge und
eine offene Teilmenge und 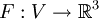 ein einmal stetig-differenzierbares Vektorfeld. Weiter sei
ein einmal stetig-differenzierbares Vektorfeld. Weiter sei 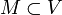 eine 2-dimensionale Untermannigfaltigkeit, die durch ein Einheitsnormalenfeld ν orientiert ist, und G eine (stückweise) glatt berandete kompakte Teilmenge von M. Die von M induzierte Orientierung auf den Rand von G wird durch des Einheitstangentialfeld τ repräsentiert. Dann gilt
eine 2-dimensionale Untermannigfaltigkeit, die durch ein Einheitsnormalenfeld ν orientiert ist, und G eine (stückweise) glatt berandete kompakte Teilmenge von M. Die von M induzierte Orientierung auf den Rand von G wird durch des Einheitstangentialfeld τ repräsentiert. Dann gilt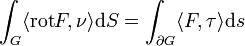 .
.
Die Form dS ist das Volumenelement bezüglich der Untermannigfaltigkeit M. In dem Fall, dass M eine reelle Teilmenge ist, hat das Volumenelement die gewohnte Form dxdy.
Beispiel
Es sei S eine Fläche, welche den Anforderungen des Satzes genügt und F = (v1,v2,0) ein Vektorfeld. So ist ein Einheitsnormalenfeld ν gegeben durch ν = (0,0,1) und es gilt
Nach dem Satz von Stokes gilt
Dieses Beispiel zeigt, dass der Satz von Green ein Spezialfall des Stokes'schen Integralsatzes ist.
Allgemeiner Integralsatz von Stokes
Sei M eine orientierte n-dimensionale differenzierbare Mannigfaltigkeit mit abschnittsweise glattem Rand
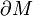 mit induzierter Orientierung. Dies ist für die meisten anschaulichen Beispiele, wie die Vollkugel mit Rand (Sphäre), gegeben.
mit induzierter Orientierung. Dies ist für die meisten anschaulichen Beispiele, wie die Vollkugel mit Rand (Sphäre), gegeben.Sei ferner ω eine alternierende Differentialform vom Grad n-1, die als stetig differenzierbar vorausgesetzt wird.
Dann gilt
wobei d die Cartan-Ableitung bezeichnet (konkret:
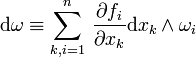 , falls
, falls 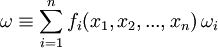 gilt, mit (n-1)-dimensionalen Basisformen
gilt, mit (n-1)-dimensionalen Basisformen 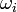 . Den allgemeinsten Fall bekommt man, wenn ωi eines der n von Null verschiedenen Differential-Produkte ist, die man erhält, wenn man in dem Ausdruck
. Den allgemeinsten Fall bekommt man, wenn ωi eines der n von Null verschiedenen Differential-Produkte ist, die man erhält, wenn man in dem Ausdruck 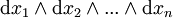 eines der Elementardifferentiale dxν streicht, und zwar das mit ν = i. Ferner ist natürlich
eines der Elementardifferentiale dxν streicht, und zwar das mit ν = i. Ferner ist natürlich 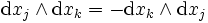 , für i, j, k, ν = 1,...,n.
, für i, j, k, ν = 1,...,n.Folgerung
Sei
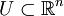 offen und ω eine stetig differenzierbare (k-1)-Form in U. Dann gilt für jede orientierte kompakte k-dimensionale Untermannigfaltigkeit
offen und ω eine stetig differenzierbare (k-1)-Form in U. Dann gilt für jede orientierte kompakte k-dimensionale Untermannigfaltigkeit 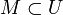
∫ dω = 0. M Beispiel
In
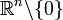 betrachten wir die (n-1)-Form
betrachten wir die (n-1)-FormAuf Grund des Stokes'schen Integralsatzes gilt
Dabei bezeichnet
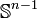 die (n-1)-dimensionale Einheitsphäre und Bn den n-dimensionalen Einheitsball.
die (n-1)-dimensionale Einheitsphäre und Bn den n-dimensionalen Einheitsball.Zugrunde liegendes topologisches Prinzip
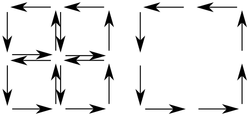
Hinter dem Satz steckt ein allgemeines topologisches Prinzip, das in seiner einfachsten Form besagt, dass sich bei „orientierter Pflasterung eines Flächenstücks“ im Innern die Wege „wegen Gegenverkehrs“ paarweise aufheben, so dass nur die Randkurve übrig bleibt.
Links in der Skizze sieht man vier kleine gleich orientierte „Pflastersteine“. Die in der Mitte eingezeichneten „inneren Wege“ werden paarweise in entgegengesetzter Richtung durchlaufen; ihre Beiträge zum Linienintegral heben sich deshalb gegenseitig auf, so dass nur der Beitrag der Randkurve übrigbleibt. Es genügt also, die Integralsätze nur für möglichst kleine „Pflastersteine“ zu beweisen.
Bei hinreichender Verfeinerung der Pflasterung ist das im Allgemeinen sehr einfach.
Spezialfälle
Mehrere Spezialfälle des allgemeinen Satzes von Stokes sind in der klassischen Vektoranalysis von Bedeutung. Dazu gehört natürlich auch der klassische Satz von Stokes, welcher im ersten Abschnitt schon behandelt wurde. Außerdem sind auch der Hauptsatz der Differential- und Integralrechnung, der Satz von Green und der Gauß'sche Integralsatz Spezialfälle des Stokes'schen Satzes.
Hauptsatz der Differential- und Integralrechnung
Sei
![]a,b[ \subset \R](/pictures/dewiki/98/b325f92eebe54da469d6ffc5737b0619.png) ein offenes Intervall und sei
ein offenes Intervall und sei ![f \colon ]a,b[ \to \R](/pictures/dewiki/98/b877964696acedfc796cbe2d8af02c14.png) eine stetig differenzierbare Funktion, so ist f(x)dx eine 1-Form bzw. Pfaff'sche Form so entartet der Stokes'sche Integralsatz zu
eine stetig differenzierbare Funktion, so ist f(x)dx eine 1-Form bzw. Pfaff'sche Form so entartet der Stokes'sche Integralsatz zuDies ist Hauptsatz der Differential- und Interalrechnung.
Gauß'scher Integralsatz
Für eine kompakte Teilmenge V des
 und ein n-dimensionales Vektorfeld F erhält man als einen weiteren Spezialfall den gaußschen Integralsatz.
und ein n-dimensionales Vektorfeld F erhält man als einen weiteren Spezialfall den gaußschen Integralsatz.Dabei ist ν der n-dimensionale Normalen-Einheitsvektor und die Integrale sind jetzt n- bzw. (n-1)-dimensional. Man kann diesen Satz als Aussage über die Divergenz eines Vektorfeldes auffassen.
Bedeutung
Der Satz von Stokes ist von fundamentaler Bedeutung in der Differentialgeometrie. Darüber hinaus finden er und seine Spezialfälle in vielen Bereichen der Physik Anwendung, beispielsweise in der Elektrodynamik.
Weblinks
Literatur
- Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8
Wikimedia Foundation.

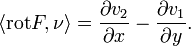
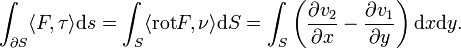
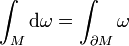
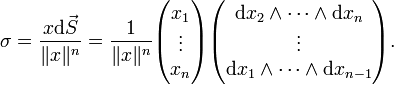
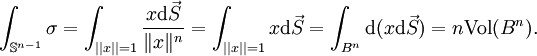
![\int_{]a,b[}\mathrm{d}f(x) = \int_{]a,b[}\frac{\mathrm{d}f}{\mathrm{d} x}(x)\, \mathrm{d}x = \left. f(x)\right|_a^b = f(b) - f(a).](/pictures/dewiki/53/5c1a69b908bcee51fc600bb67e56d770.png)