Satz von Stokes

Der Satz von Stokes oder stokesscher Integralsatz ist ein nach Sir George Gabriel Stokes benannter Satz aus der Differentialgeometrie. In der allgemeinen Fassung handelt es sich um einen sehr tiefliegenden Satz über die Integration von Differentialformen, der den Hauptsatz der Differential- und Integralrechnung erweitert und eine Verbindungslinie von der Differentialgeometrie zur Algebraischen Topologie eröffnet. Dieser Zusammenhang wird durch den Satz von de Rham beschrieben, für den der Satz von Stokes grundlegend ist.

Es geht darum, n-dimensionale Volumenintegrale über das Innere in (n-1)-dimensionale Randintegrale über die Oberfläche des Volumenstücks umzuwandeln. Häufig werden nur spezielle Varianten des allgemeinen Satzes betrachtet, aus denen das allgemeine Prinzip mehr oder minder gut ersichtlich ist, die aber für die jeweiligen Anwendungen wichtig sind. Die beiden wichtigsten Spezialfälle, der Gauß'sche Integralsatz und der spezielle Stokes'sche Integralsatz (siehe unten) entstammen der Vektoranalysis. In der Physik und der Elektrotechnik erlaubt der spezielle Satz von Stokes beziehungsweise der von Gauß elegante Schreibweisen physikalischer Zusammenhänge, zum Beispiel bei den integrierten Formen der Maxwell'schen Gleichungen.

Integralsatz von Stokes

Aussage

Sei M eine orientierte n-dimensionale differenzierbare Mannigfaltigkeit mit abschnittsweise glattem Rand $\partial M$ mit induzierter Orientierung. Dies ist für die meisten anschaulichen Beispiele, wie die Vollkugel mit Rand (Sphäre) oder den Torus (Rettungsring), gegeben.

Sei ferner ω eine auf M (bzw. in einer hinreichend großen offenen Umgebung) definierte alternierende Differentialform vom Grad n−1, die als stetig differenzierbar vorausgesetzt wird.

Dann gilt die folgende Aussage, die nach Stokes benannt wurde:

$\int_M \mathrm{d}\omega = \int_{\partial M} \omega$

wobei d die Cartan-Ableitung bezeichnet. Das rechte Integral kann man als Oberflächenintegral verstehen oder allgemeiner als Integral über die Mannigfaltigkeit $\partial M$.

Die Cartan-Derivation „dω“ ist hier gewissermaßen „dual“ zu der topologischen Operation $\partial M$, wodurch sich die in dieser Formel enthaltene Querbeziehung zwischen Aspekten der Analysis und topologisch-algebraischen Aspekten ergibt.

Anmerkungen

Ein Normalgebiet

Unter der sehr allgemeinen Voraussetzung, dass $\textstyle \omega\equiv \sum_{i=1}^{n} f_i(x_1,x_2,...,x_n)\,\omega_i$   gilt, - mit (n−1)-dimensionalen Basisformen ω_i, zum Beispiel mit $\omega_1=\rm dx_2\wedge \rm dx_3\wedge ...\,\wedge\rm dx_{n-1}\wedge \rm dx_n\,,\,\, \omega_2=\rm dx_3\wedge\rm dx_4 \wedge ...\,\wedge\rm dx_n\wedge\rm dx_1,\, ...\,,$ und mit dem „wedge- Produkt“ $\wedge$, das unter anderem die Bedingung der Antisymmetrie erfüllt, $-\rm dx_k\wedge\rm dx_i=\rm dx_i\wedge\rm dx_k$, besagt die äußere Ableitung konkret das Folgende:

$\textstyle \mathrm{d}\omega \equiv\sum_{k,i=1}^n\,{\frac{\partial f_i}{\partial x_k}}\mathrm{d}x_k\wedge\omega_i\,.$

Besonders einfach wird der Beweis des „Hauptsatzes“, wenn wie beim nebenstehenden Beispiel eines Normalgebietes die Integrationsmannigfaltigkeit (in der Zeichnung D genannt) in vertikale Streifen (in x_n-Richtung) so segmentiert werden kann, dass nur an der gelb eingezeichneten „Oberseite“ und an der rot eingezeichneten „Unterseite“ nichttriviale Beiträge entstehen, und zwar wegen der ebenfalls eingezeichneten Orientierung (die Pfeilrichtungen) mit entgegengesetztem Vorzeichen.

Folgerung

Sei $U \subset \R^n$ offen und ω eine stetig differenzierbare (k-1)-Form in U. Dann gilt für jede orientierte kompakte k-dimensionale Untermannigfaltigkeit $M \subset U$ die Aussage:

∫	dω = 0.
M

Anwendungen

Der (allgemeine) Satz von Stokes wird vor allem in der Mathematik verwendet. Er

• enthält als Spezialfälle für Physiker und Elektro-Ingenieure den Satz von Gauß und den speziellen Satz von Stokes (siehe unten), und
• bildet zweitens eine konkrete Verbindung zwischen differentialgeometrischen und algebraischen Aspekten der Topologie, indem etwa in einer differenzierbaren Mannigfaltigkeit zwei verschiedene Wege $\mathcal W_1$ und $\mathcal W_2$, die vom gleichen Anfangspunkt ausgehen und zum gleichen Endpunkt führen, als topologisch homolog definiert werden, wenn für gewisse einstufige Differentialformen ω das Kurvenintegral $\textstyle \oint_{\,\mathcal W_1-\mathcal W_2}\,\omega$ verschwindet. Entsprechende Begriffe der algebraischen Topologie kann man auch mit dem höherdimensionalen Stokes'schen Satz aufbauen.

Integralsatz von Stokes für Ketten

Integration über Ketten

Sei $\sigma : \Delta_p \to M$ ein glatter p-Simplex und ω eine glatte, geschlossene Differentialform auf der glatten Mannigfaltigkeit M. Dann ist das Integral über σ definiert durch

$\int_\sigma \omega = \int_{\Delta_p} \sigma^*\omega$.

Dabei bezeichnet σ ^* ω den Rücktransport von ω bezüglich σ. Die Definition ergibt Sinn, da Δ_p eine glatte Untermannigfaltigkeit mit Rand und induzierter Orientierung von $\R^p$ ist. (Oder man versteht Δ_p einfach als abgeschlossene Teilmenge des $\R^p$.) Im Fall p = 1 entspricht die Definition dem gewöhnlichen Kurvenintegral. Ist $\textstyle c = \sum_{i=1}^k c_i \sigma_i$ eine glatte p-Kette des singulären Komplexes, dann ist das Integral von ω über c definiert als

$\int_c \omega := \sum_{i=1}^k c_i \int_{\sigma_i} \omega = \sum_{i=1}^k c_i \int_{\Delta_p} \sigma_i^*\omega.$

Für den Fall p = 1 findet man die Definition und weitere Informationen im Artikel Zyklus (Funktionentheorie).

Aussage

Sei c eine glatte p-Kette des singulären Komplexes und ω eine glatte (p-1)-Differentialform auf der glatten Mannigfaltigkeit M. Dann gilt

$\int_{\partial c} \omega = \int_c \mathrm{d} \omega.$

Mit $\partial \colon C_p \to C_{p-1}$ wird der Randoperator des singulären Komplexes bezeichnet.

Anwendung

Dieser Satz zeigt eine Verbindung zwischen differentialgeometrischen und topologischen Eigenschaften einer glatten Mannigfaltigkeit auf. Betrachtet man nämlich die De-Rham-Kohomologie $H_{dR}^*(M)$ und die singuläre Homologie $H^\text{sing}_*(M)$ von M, so erhält man durch

$\begin{align} J \colon H^p_{dR}(M) &\to \operatorname{Hom}(H_p^\text{sing}(M),\R) \\ \omega &\mapsto \left(c \mapsto \int_c \omega \right) \end{align}$

mit $c \in H_p^\text{sing}(M)$ einen Homomorphismus. Aufgrund des Satzes von Stokes ist dieser Homomorphismus wohldefiniert und es kommt nicht auf die Wahl des Repräsentanten c der Homologieklasse an. Seien c₁ und c₂ zwei Repräsentanten der gleichen singulären Homologieklasse, dann gilt $c_1 - c_2 = \partial b$, denn zwei Repräsentanten unterscheiden sich nur um ein Element des Randes. Daher folgt mit dem Satz von Stokes

$\int_{c_1} \omega - \int_{c_2} \omega = \int_{\partial b} \omega = \int_b \mathrm{d} \omega = 0.$

Die letzte Gleichheit gilt, da ω ein Element der De-Rham-Kohomologie ist und daher dω = 0 gilt. Ist ω = dν eine exakte Differentialform dann gilt

$\int_c \omega = \int_c \mathrm{d} \nu = \int_{\partial c} \nu = 0.$

Nach dem zentralen Satz von de Rham ist der Homomorphismus sogar ein Isomorphismus.

Zugrunde liegendes topologisches Prinzip

Hinter dem Stokes'schen Satz steckt ein allgemeines topologisches Prinzip, das in seiner einfachsten Form besagt, dass sich bei „orientierter Pflasterung eines Flächenstücks“ im Innern die Wege „wegen Gegenverkehrs“ paarweise aufheben, so dass nur die Randkurve übrig bleibt.

Pflasterung

Links in der Skizze sieht man vier kleine gleich orientierte „Pflastersteine“. Die in der Mitte eingezeichneten „inneren Wege“ werden paarweise in entgegengesetzter Richtung durchlaufen; ihre Beiträge zum Linienintegral heben sich deshalb gegenseitig auf, so dass nur der Beitrag der Randkurve übrigbleibt. Es genügt also, die Integralsätze nur für möglichst kleine „Pflastersteine“ zu beweisen.

Bei hinreichender Verfeinerung der Pflasterung ist das im Allgemeinen fast elementar.

Spezialfälle

Mehrere Spezialfälle des allgemeinen Satzes von Stokes sind in der klassischen Vektoranalysis von Bedeutung. Dazu gehört natürlich der klassische Satz von Stokes. Er folgt aus dem allgemeinen Satz mit ω:=F₁dx₁+F₂dx₂+F₃dx₃. Außerdem sind auch der Hauptsatz der Differential- und Integralrechnung, der Satz von Green und der Gauß'sche Integralsatz Spezialfälle des allgemeinen Stokes'schen Satzes. Der Gauß'sche Satz ergibt sich z. B. für ω:=F₁dx₂$\wedge$dx₃...$\wedge$dx_n-1$\wedge$dx_n+F₂dx₃$\wedge$dx₄...$\wedge$dx_n$\wedge$dx₁+... .

Hauptsatz der Differential- und Integralrechnung

Sei $(a,b) \subset \R$ ein offenes Intervall und $f \colon [a,b] \to \R$ eine stetig differenzierbare Funktion. Dann ist df(x) eine 1-Form (sog. Pfaff'sche Form), und der allgemeine Stokes'sche Integralsatz entartet zu

$\int_a^b\mathrm{d}f(x) = \int_a^b\frac{\mathrm{d}f}{\mathrm{d} x}(x)\, \mathrm{d}x = \left. f(x)\right|_a^b = f(b) - f(a).$

Dies ist der Hauptsatz der Differential- und Integralrechnung.

Gaußscher Integralsatz

→ Hauptartikel: Gaußscher Integralsatz

Für eine kompakte Teilmenge V des $\mathbb{R}^n$ und ein n-dimensionales Vektorfeld F erhält man als einen weiteren Spezialfall den gaußschen Integralsatz.

$\int_{V} \operatorname{div}F \,\mathrm{d}V = \oint_{\partial V} \langle F, \nu\rangle \, \mathrm{d} S$

Im Dreidimensionalen schreibt man auch explizit

$\iiint_V\operatorname{div} F\,\mathrm{d}V=\iint_{\partial V}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\;\;\;\subset\!\supset \,\,F \cdot \mathrm{d} S$

Dabei ist ν der n-dimensionale Normalen-Einheitsvektor und die Integrale sind jetzt n- beziehungsweise (n−1)-dimensional, wobei die Größe $\operatorname{div} F$ auch als $\nabla\cdot F$ geschrieben wird. Man kann diesen Satz auch zur Definition der Divergenz eines Vektorfeldes benutzen, wobei diese Definition unabhängig von den benutzten Koordinaten ist.

Klassischer Integralsatz von Stokes

Zum klassischen Satz von Stokes: Dargestellt ist die (gekrümmte) Fläche Σ, deren Randkurve $\partial \Sigma$ (angedeutet durch die Pfeile) und der Normalenvektor n (im Text ν genannt).

George Stokes

William Thomson (= Lord Kelvin)

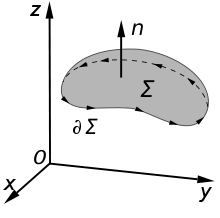
Der klassische Integralsatz von Stokes ist auch als Satz von Kelvin-Stokes oder Rotationssatz bekannt. Er findet bei Physikern und Elektrotechnikern Anwendung vor allem im Zusammenhang mit den Maxwell'schen Gleichungen. Er besagt, dass ein Flächenintegral über die Rotation eines Vektorfeldes in ein geschlossenes Kurvenintegral über die Tangentialkomponente des Vektorfeldes umgewandelt werden kann. Dies ist hilfreich, da das Kurvenintegral das Vektorfeld allein enthält und in der Regel einfacher zu berechnen ist als Flächenintegrale, zumal dann, wenn die betrachtete Fläche gekrümmt ist. Darüber hinaus sind die Kurvenintegrale in vielen Anwendungen unmittelbar betroffen - und erst in zweiter Linie die zugehörigen Flächenintegrale - zum Beispiel beim faradayschen Induktionsgesetz. Ist speziell $\partial \Sigma$ gegeben, so führt die Tatsache, dass viele verschiedene Mannigfaltigkeiten Σ in eine einzige geschlossene Randmannigfaltigkeit $\partial \Sigma$  „eingezwängt“ werden können, zu der Eichinvarianz von Theorien wie der von Maxwell.

Aussage

Es sei $V \subset \R^3$ eine offene Teilmenge des dreidimensionalen Raumes und $F : V \to \R^3$ ein auf V definiertes einmal stetig differenzierbares Vektorfeld. Dies wird gefordert, damit der Ausdruck $\operatorname{rot}(F)$ gebildet werden kann. Weiter sei $\Sigma \subset V$ eine in V enthaltene zweidimensionale reguläre Fläche, die durch ein Einheitsnormalenfeld $\mathbf\nu$ orientiert ist (das heißt, es sei definiert, was die „Oberseite“ der Fläche ist). Außerdem ist τ der Tangenteneinheitsvektor der Randkurve. Mit der Eigenschaft regulär wird sichergestellt, dass der Rand hinreichend glatt ist.

Der Rand von Σ wird mit $\partial \Sigma$ bezeichnet. Im Folgenden wird dieser Rand $\partial \Sigma$ stets mit einer geschlossenen Kurve identifiziert. Mit all diesen Voraussetzungen gilt

$\int_\Sigma \langle \operatorname{rot}\, F, \mathbf\nu \rangle \,\mathrm{d} S = \oint_{\partial \Sigma} \langle F, \mathbf\tau\rangle \,\mathrm{d} s$.

In den Anwendungen schreibt man auch

$\iint_{\Sigma\,\subset \,\mathbb R^3}\mathrm{rot}(F) \cdot \mathrm{d} S = \oint_{\partial\Sigma} F\cdot\mathrm d r$,

mit $\mathrm d S= \nu\,\mathrm{dS}$ und $\mathrm d r= \tau\,\mathrm{ds}$. Ferner ist $\operatorname{rot} F$ die Rotation, und $\langle V_1, V_2\rangle$ (beziehungsweise $V_1\cdot V_2$) das Skalarprodukt der zwei Vektoren V₁,V₂. Die Form dS ist die Volumenform der zweidimensionalen Fläche Σ und ds ist das Längenelement der Randkurve.

Anmerkungen

In dem Fall, dass Σ eine flache Teilmenge darstellt, gilt in geeigneten Koordinaten $\mathrm dS\equiv\mathrm{d} x \mathrm{d}y$. Ist Σ nicht flach, so lässt sich unter der Voraussetzung, dass sich die zweidimensionale Fläche mit der Parametrisierung

$r(u,v)_{\,|i}=\{x(u,v), \,\,y(u,v), z(u,v)\}_{\,|i}$ mit $a_{\,i}\le u\le b_{\,i}\,\,,c_{\,i}\le v\le d_{\,i}\,, i=1,\ldots,N$

in N Segmente zerlegen lässt, die Volumenform für festes i durch

$\textstyle \mathrm dS\equiv\sqrt{\left(\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial y}{\partial u}\frac{\partial x}{\partial v}\right )^2 + \left(\frac{\partial y}{\partial u}\frac{\partial z}{\partial v}-\frac{\partial z}{\partial u}\frac{\partial y}{\partial v}\right )^2 + \left(\frac{\partial z}{\partial u}\frac{\partial x}{\partial v}-\frac{\partial x}{\partial u}\frac{\partial z}{\partial v}\right )^2\,}\mathrm du\mathrm dv$

berechnen. Auch der Vektor ν lässt sich analog berechnen, und zwar ist ν der aus den drei Komponenten des Vektorprodukts $\boldsymbol a=\tfrac{\partial r}{\partial u} \times \tfrac{\partial r}{\partial v}$ gebildete Einheitsvektor, das heißt

$a_1=\frac{\partial y}{\partial u}\frac{\partial z}{\partial v} - \frac{\partial z}{\partial u}\frac{\partial y}{\partial v},\ a_2=\frac{\partial z}{\partial u}\frac{\partial x}{\partial v} - \frac{\partial x}{\partial u}\frac{\partial z}{\partial v},\ a_3=\frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial y}{\partial u}\frac{\partial x}{\partial v}$.

Beispiel

Es sei Σ eine als Normalgebiet bezeichnete flache Mannigfaltigkeit, welche den Anforderungen des Satzes genügt, und das Vektorfeld F gegeben durch $\,F = (v_1, v_2, 0)$. Das Einheitsnormalenfeld ν sei gegeben durch $\,\nu = (0 , 0 , 1)\,.$ Dann gilt

$\langle \operatorname{rot} F , \nu \rangle = \frac{\partial v_2}{\partial x} - \frac{\partial v_1}{\partial y}.$

Nach dem Satz von Stokes gilt

$\oint_{\partial \Sigma} \langle F, \tau \rangle \,\mathrm{d} s = \iint_\Sigma \langle \operatorname{rot} \,F, \nu \rangle \,\mathrm{d} S = \iint_\Sigma\left( \frac{\partial v_2}{\partial x} - \frac{\partial v_1}{\partial y} \right) \mathrm{d} x \mathrm{d} y.$

Dieses Beispiel zeigt, dass der Satz von Green ein Spezialfall des stokesschen Integralsatzes ist.

Literatur

• Herbert Amann, Joachim Escher: Analysis 3. Birkhäuser Verlag, Berlin 2001, ISBN 978-3-7643-8883-6.
• Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg 2000, ISBN 3-540-43580-8.
• John M. Lee: Introduction to Smooth Manifolds. Springer-Verlag, 2. Aufl., New York 2003, ISBN 0-387-95448-1.
• Hans Grauert, Ingo Lieb, Wolfgang Fischer: Differential- und Integralrechnung. Insbesondere Bd. 3: Integrationstheorie. Kurven- und Flächenintegrale. Springer-Verlag, Heidelberger Taschenbücher 1977, ISBN 3-540-08697-8.