- Integritätsbereich
-
In der Algebra ist ein Integritätsring oder Integritätsbereich ein nullteilerfreier kommutativer Ring mit einem Einselement, das von Null verschieden ist.
Alternativ kann man einen Integritätsring definieren als einen kommutativen Ring mit 1, in dem das Nullideal {0} ein Primideal ist, oder als einen Teilring eines Körpers. Es gibt auch eine abgeschwächte Definition, in der kein Einselement gefordert wird, sondern nur, dass es wenigstens ein von Null verschiedenes Element in dem Ring gibt. Ein Großteil der Sätze über Integritätsringe benötigen jedoch eine Eins, deshalb wird diese Eigenschaft meist mit in die Definition aufgenommen.
Inhaltsverzeichnis
Beispiele
Das bekannteste Beispiel ist der Ring
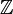 der ganzen Zahlen.
der ganzen Zahlen.Jeder Körper ist ein Integritätsring. Umgekehrt ist jeder artinsche Integritätsring ein Körper. Insbesondere ist jeder endliche Integritätsring ein endlicher Körper.
Ein Polynomring ist ein Integritätsring, wenn die Koeffizienten aus einem Integritätsring stammen. Zum Beispiel ist der Ring
![\Z[X]](/pictures/dewiki/100/dba144b0c7e9c5c01ae1a1d569bfea39.png) der Polynome mit ganzzahligen Koeffizienten ein Integritätsring, ebenso wie der Ring
der Polynome mit ganzzahligen Koeffizienten ein Integritätsring, ebenso wie der Ring ![\R[X,Y]](/pictures/dewiki/50/2a18f9bd780357c6089a42936e95d1e3.png) der reellen Polynome in zwei Variablen.
der reellen Polynome in zwei Variablen.Der Ring aller reellen Zahlen der Form
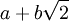 mit ganzen Zahlen a,b ist ein Integritätsring, da er Teilring von
mit ganzen Zahlen a,b ist ein Integritätsring, da er Teilring von  ist.
ist.Ist
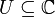 ein Gebiet (eine zusammenhängende offene Teilmenge) in den komplexen Zahlen, so ist der Ring
ein Gebiet (eine zusammenhängende offene Teilmenge) in den komplexen Zahlen, so ist der Ring 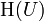 der holomorphen Funktionen
der holomorphen Funktionen 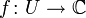 ein Integritätsring.
ein Integritätsring.Ist R ein kommutativer Ring mit 1 und P ein Primideal in R, so ist der Faktorring R / P ein Integritätsring.
Der Restklassenring
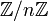 ist genau dann ein Integritätsring, sogar ein Körper, wenn n eine Primzahl ist.
ist genau dann ein Integritätsring, sogar ein Körper, wenn n eine Primzahl ist.Teilbarkeit, Primelemente, Irreduzibilität
- (Hauptartikel: Teilbarkeit)
Sind a und b Elemente des Integritätsrings R, dann nennt man a einen Teiler von b und b ein Vielfaches von a (und sagt auch a teile b), wenn es ein Element x in R gibt, sodass ax = b. Man schreibt dann
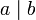 , andernfalls
, andernfalls 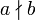 .
.Es gelten die folgenden Teilbarkeitsregeln:
- Gilt
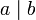 und
und 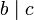 , dann folgt daraus
, dann folgt daraus 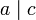 .
. - Gilt
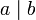 , dann gilt auch
, dann gilt auch 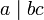 für jedes
für jedes 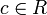 , insbesondere auch
, insbesondere auch 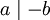 .
. - Gilt
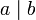 und
und 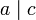 , dann gilt auch
, dann gilt auch 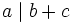 und
und 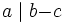 .
.
Die erste Regel besagt, dass Teilbarkeit transitiv ist. Die zweite und dritte Regel besagen, dass die Menge aR der Vielfachen eines Elementes a ein Ideal in R bildet; dieses wird auch als (a) notiert.
Ringelemente, die Teiler der 1 sind, heißen Einheiten von R. Die Einheiten sind identisch mit den invertierbaren Elementen und teilen alle anderen Elemente. Die Menge der Einheiten von R wird mit R * bezeichnet und bildet zusammen mit der Ringmultiplikation als Verknüpfung eine abelsche Gruppe – die sogenannte Einheitengruppe von R.
Gilt
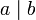 und
und 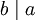 , dann heißen a und b zueinander assoziiert. a und b sind genau dann assoziiert, wenn es eine Einheit u gibt, sodass au = b.
, dann heißen a und b zueinander assoziiert. a und b sind genau dann assoziiert, wenn es eine Einheit u gibt, sodass au = b.Ist q eine Nichteinheit, dann heißt q irreduzibel, falls q nicht als Produkt zweier Nichteinheiten darstellbar ist, falls also aus q = ab stets
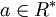 oder
oder 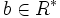 folgt. Ist p eine Nichteinheit ungleich 0, dann heißt p prim (oder Primelement), falls gilt: Aus
folgt. Ist p eine Nichteinheit ungleich 0, dann heißt p prim (oder Primelement), falls gilt: Aus 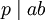 folgt
folgt 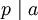 oder
oder 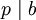 . Das Hauptideal (p) ist dann ein Primideal. Ist andersherum das Hauptideal (p) einer von Null verschiedenen Nichteinheit p ein Primideal, so ist p prim.
. Das Hauptideal (p) ist dann ein Primideal. Ist andersherum das Hauptideal (p) einer von Null verschiedenen Nichteinheit p ein Primideal, so ist p prim.Jedes Primelement ist irreduzibel (für diese Aussage wird die Nullteilerfreiheit des Rings benötigt), aber nicht immer ist jedes irreduzible Element prim (z. B. im Ring
![\mathbb Z[\sqrt{-3}]](/pictures/dewiki/53/5549c5ad93d9f03bb9d826197a6dcc79.png) sind 2,
sind 2, 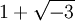 und
und 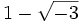 irreduzibel aber nicht prim). In Hauptidealringen und allgemeiner in faktoriellen Ringen stimmen jedoch beide Begriffe überein. So werden in
irreduzibel aber nicht prim). In Hauptidealringen und allgemeiner in faktoriellen Ringen stimmen jedoch beide Begriffe überein. So werden in 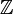 die Primzahlen üblicherweise nur als positive, irreduzible Elemente von
die Primzahlen üblicherweise nur als positive, irreduzible Elemente von 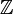 definiert. Diese Elemente sind jedoch auch Primelemente, da
definiert. Diese Elemente sind jedoch auch Primelemente, da 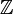 faktoriell und somit jedes irreduzible Element prim ist. Es sind jedoch auch noch die negativen Pendants der Primzahlen Primelemente, woran man sieht, dass der Begriff des Primelements allgemeiner gefasst ist als der Begriff der Primzahl.
faktoriell und somit jedes irreduzible Element prim ist. Es sind jedoch auch noch die negativen Pendants der Primzahlen Primelemente, woran man sieht, dass der Begriff des Primelements allgemeiner gefasst ist als der Begriff der Primzahl.Quotientenkörper
Ist R ein Integritätsring, dann existiert ein kleinster Körper
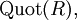 der R als Teilring enthält. Der Körper
der R als Teilring enthält. Der Körper 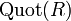 ist bis auf Isomorphie eindeutig bestimmt und heißt Quotientenkörper von R. Seine Elemente haben die Form
ist bis auf Isomorphie eindeutig bestimmt und heißt Quotientenkörper von R. Seine Elemente haben die Form 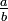 mit
mit 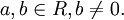 Der Quotientenkörper ist ein Beispiel einer Konstruktion mit einem Integritätsring, in dem keine Eins (in der Definition des Integritätsringes) benötigt wird, sondern lediglich irgendein von Null verschiedenes Element.
Der Quotientenkörper ist ein Beispiel einer Konstruktion mit einem Integritätsring, in dem keine Eins (in der Definition des Integritätsringes) benötigt wird, sondern lediglich irgendein von Null verschiedenes Element.Der Quotientenkörper des Rings der ganzen Zahlen ist der Körper der rationalen Zahlen. Der Quotientenkörper eines Körpers ist der Körper selbst.
Alternativ kann man Quotientenkörper über Lokalisierungen von R nach dem Nullideal {0} konstruieren.
Abstrakt definiert man Quotientenkörper durch folgende universelle Eigenschaft:
- Ein Quotientenkörper eines Ringes R ist ein Paar (K,φ) aus einer Menge K und einem Ringhomomorphismus φ von R nach K mit der Eigenschaft, dass es für jeden Körper L mit Ringhomomorphismus
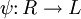 genau einen Körperhomomorphismus
genau einen Körperhomomorphismus 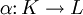 mit
mit 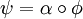 gibt.
gibt.
Charakteristik
Die Charakteristik eines Integritätsrings ist entweder 0 oder eine Primzahl.
Ist R ein Integritätsring mit der Primzahl-Charakteristik p, dann ist die Abbildung
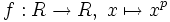 ein injektiver Ringhomomorphismus und heißt Frobeniushomomorphismus.
ein injektiver Ringhomomorphismus und heißt Frobeniushomomorphismus.Literatur
- Bosch: Algebra. 5. Auflage. Springer, 2003, ISBN 3-540-40388-4.
- Jantzen und Schwermer: Algebra. Springer, 2005, ISBN 3-540-21380-5.
- Kurt Meyberg: Algebra Teil 1 & 2. Carl Hanser Verlag, München 1975/76.
Wikimedia Foundation.
