- Ameisenkolonieoptimierung
-
Ameisenalgorithmen gehören zu den Metaheuristiken für Verfahren der kombinatorischen Optimierung, die auf dem modellhaften Verhalten von realen Ameisen bei der Futtersuche basieren. Die meisten Ameisenalgorithmen erfüllen auch die von Marco Dorigo vorgestellte ACO (Ant Colony Optimization)-Metaheuristik.
Inhaltsverzeichnis
Natürliches Vorbild
Bei der Futtersuche scheiden einzelne Ameisen einen Duftstoff (sog. Pheromon) aus, der andere Ameisen anzieht. Gibt es zwischen Nest und Futterquelle mehrere mögliche Wege, so wird mit der Zeit auf dem kürzesten Pfad eine höhere Pheromonkonzentration als auf den anderen vorherrschen, so dass die Ameisen bevorzugt diesen Weg wählen werden: Sie scheinen entlang einer Straße zu laufen, eine Ameisenstraße ist entstanden.
Ähnliches gibt es auch beim Menschen: Zum Beispiel wurde auf einem Campus beobachtet, wie die Fußspuren durch den Schnee verlaufen, und im Frühjahr wurden danach die Wege (Verlauf und Breite) gestaltet.
Übertragung auf Algorithmen
Dieses Vorgehen ist eine Form von Schwarmintelligenz: eine Leistung – hier als Beispiel die Lösung eines Optimierungsproblems, nämlich die Suche nach der kürzesten Route – wird durch das Zusammenspiel einer Vielzahl von wenig intelligenten und damit leicht nachprogrammierbaren Einzelakteuren wie den Ameisen hervorgebracht.
Der erste vorgestellte Ameisenalgorithmus, das so genannte Ant System (AS), wurde vom italienischen Wissenschaftler Marco Dorigo vorgestellt. Er wandte das AS auf das Problem des Handlungsreisenden an, da eine Übertragung von der Suche nach kürzesten Wegen auf dieses Problem am naheliegendsten ist.
Weitere wichtige Ameisenalgorithmen sind das Ant Colony System (ACS) von Luca Maria Gamberdella sowie das Max-Min Ant System (MMAS) von Thomas Stützle, mit dem bisher die besten Ergebnisse für das Problem des Handlungsreisenden erzielt wurden.
Mit Ameisenalgorithmen lassen sich vor allem kombinatorische Optimierungsprobleme lösen, z.B. für Projektplanungsprobleme oder das Quadratische Zuordnungsproblem, doch auch andere Aufgaben können damit angegangen werden. Wichtig ist, dass zwar Annäherungen an ein mögliches Optimum gefunden werden, allerdings in den meisten Fällen kein optimaler Wert.
Anwendungen
- Busrouten, Müllabfuhr, Post- und Auslieferungsrouten.
- Maschinenbelegungsproblem: Minimierung der Transportzeit bei räumlich weit auseinander liegenden Produktionsstätten: Realisiert bei Unilever in England und Vincent Darley von der Bios-Gruppe in Santa Fe (New Mexico)
- Beschickung von Lackieranlagen: Losbildung zur Minimierung der Farbwechsel: Realisiert bei DaimlerChrysler
- Proteinfaltung: 20 Aminosäuren werden zu Proteinen mit 100 Aminosäuren kombiniert => 20100, dies ergibt ca. 10130 verschiedene Proteine.
- Telefonnetzwerk und Internet: Durch ACO können schnell freie Strecken gefunden werden und zwar während des Betriebs (z.B. Antnet)
- Personaleinsatzplanung bei Fluggesellschaften: Flugbegleiter und Piloten werden unter Berücksichtigung von Ruhephasen etc. monatlich geplant.
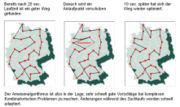
Screendump TSP mit ACO
Das Problem des Handlungsreisenden (TSP) kann sehr effizient mit ACO bearbeitet werden. Im Beispiel wird TSP mit 30 "Städten" bzw. Zielen berechnet (etwa 4,4·1030 mögliche Wege). Die Stärke von ACO, Änderungen im laufenden Suchprozess selbstadaptiv zu verarbeiten, wird im Beispiel deutlich. Bei Verschieben eines Zielpunktes in der nach 20 sec. gefundenen Route, wird bereits 10 sec. später (ohne Reinitialisierung) vom Algorithmus erneut ein guter Wegevorschlag gemacht (siehe Kombinatorik).
Siehe auch
Weblinks
- http://www.ameisenalgorithmus.de/
- http://www.carpe-retem.com/Index.php?seite=Handbuch.AntColonyOptimization
- http://www.m-boehmer.de/pdf/Schwarmintelligenz_Artikel.pdf (PDF; 640 KB)
- AntSim v1.0 Werkzeug zur Visualisierung des Ameisenalgorithmus (Windows)
- Schwarmlogistik - Was wir von den Ameisen noch lernen können: Film über die Adaption der Schwarmintelligenz in die Logistik
Wikimedia Foundation.