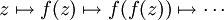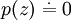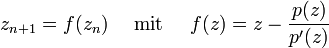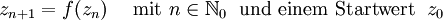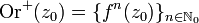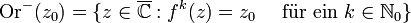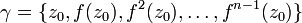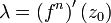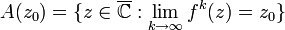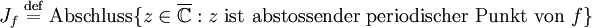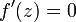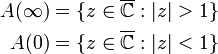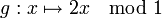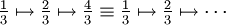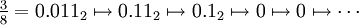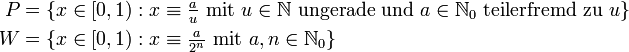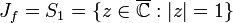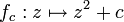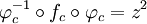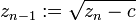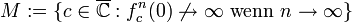- Julia-Mengen
-
Die Julia-Mengen, erstmals von Gaston Maurice Julia und Pierre Fatou beschrieben, sind Teilmengen der komplexen Zahlenebene, wobei zu jeder holomorphen oder meromorphen Funktion eine Julia-Menge gehört. Oft sind die Julia-Mengen fraktale Mengen. Das Komplement der Julia-Menge heißt Fatou-Menge.
Wendet man eine auf ganz ℂ definierte Funktion f immer wieder auf ihre Funktionswerte an, dann ergibt sich eine Folge komplexer Zahlen:
Abhängig vom Startwert z kann diese Folge zwei grundlegend verschiedene Verhalten zeigen
- Eine kleine Änderung des Startwertes führt zu praktisch der gleichen Folge, die Dynamik ist in gewissem Sinne stabil: der Startwert wird der Fatou-Menge zugeordnet.
- Eine noch so kleine Änderung des Startwertes führt zu einem komplett anderen Verhalten der Folge, die Dynamik hängt "chaotisch" vom Startwert ab: der Startwert gehört zur Julia-Menge.
Inhaltsverzeichnis
Hintergrund
Das Newton-Verfahren ist eines der bekanntesten und am weitesten verbreiteten Verfahren zur Lösung nichtlinearer Gleichungen. Hat man die zu lösende Gleichung in der Form
geschrieben, dann sind Nullstellen z einer Funktion p zu finden. Ist die Funktion p differenzierbar, dann transformiert das Newton-Verfahren das statische Problem "p(x) = 0" in einen dynamischen Prozess: es liefert eine Iterationsvorschrift der Gestalt
mit folgenden Eigenschaften
- Die Nullstellen von p werden zu anziehenden Fixpunkten von f
- Liegt der Startwert z0 der Iteration nahe an einer Nullstelle von p, dann konvergiert die Newton-Iteration gegen den zugehörenden Fixpunkt von f, und damit gegen diese Nullstelle.
Man muss also nur eine ungefähre Lösung des Problems haben. Die Fixpunkte agieren dabei ähnlich wie die Zentren von Kraftfeldern, die Teilchen in ihrer Nähe anziehen. Mit jedem Iterationsschritt wandern die Teilchen näher zur Kraftquelle.
Von seiner Konzeption her ist das Newton-Verfahren – wie andere Fixpunktiterationen auch – also ein lokales Verfahren, dessen Verhalten bekannt ist, wenn man sich nahe an einer Nullstelle befindet. Was geschieht jedoch, wenn wir uns weiter von den Anziehungspunkten entfernen, und wie sehen die Grenzen zwischen den Einzugsbereichen der einzelnen Kraftquellen aus?
 Julia-Menge der Newton-Iteration (das Newton-Fraktal) eines kubischen Polynoms. Die türkis-, pink- und beigefarbene Bereiche sind die drei Einzugsgebiete der drei Nullstellen des Polynoms. Startwerte aus den schwarz-roten Gebieten werden von einem Zyklus der Länge 2 angezogen, konvergieren also nicht gegen eine Nullstelle. Startwerte aus der weißen Julia-Menge, welche die Grenze zwischen den einzelnen Einzugsbereichen bildet, konvergieren ebenfalls nicht gegen eine Nullstellen, sie hüpfen wild umher.
Julia-Menge der Newton-Iteration (das Newton-Fraktal) eines kubischen Polynoms. Die türkis-, pink- und beigefarbene Bereiche sind die drei Einzugsgebiete der drei Nullstellen des Polynoms. Startwerte aus den schwarz-roten Gebieten werden von einem Zyklus der Länge 2 angezogen, konvergieren also nicht gegen eine Nullstelle. Startwerte aus der weißen Julia-Menge, welche die Grenze zwischen den einzelnen Einzugsbereichen bildet, konvergieren ebenfalls nicht gegen eine Nullstellen, sie hüpfen wild umher.Ernsthafte Untersuchungen über die globale Dynamik des Verfahrens reichen zurück bis ins Jahre 1879, als Lord Arthur Cayley das Problem von den reellen Zahlen auf die komplexen Zahlen ausdehnte und globale Untersuchungen vorschlug:
- In connexion herewith, throwing aside the restrictions as to reality, we have what I call the Newton-Fourier Imaginary Problem. [...] The problem is to determine the regions of the plane, such that P being taken at pleasure anywhere within one region we arrive ultimately at the point A; anywhere within another region at the point B; and so for the several points representing the roots of the equation.[1]
Dabei stieß er jedoch schon für den Fall, dass p ein Polynom dritten Grades ist, auf unüberwindliche Probleme, so dass er seine Untersuchungen schließlich einstellte:
- The solution is easy and elegant in the case of a quadratic equation, but the next succeeding case of the cubic equation appears to present considerable difficulty.
Vor diesem Hintergrund entwickelten die Franzosen Pierre Fatou und Gaston Julia zu Beginn des 20. Jahrhunderts ihre Theorie der Iterationen rationaler Funktionen in der komplexen Ebene, das heißt die Theorie diskreter dynamischer Systeme der Form
mit einer meromorphen Funktion f. Dazu wird jedoch nicht die Standardmetrik der Ebene verwendet. Stattdessen wird die komplexe Zahlenebene mittels einer stereographischen Projektion auf die Oberfläche einer Kugel projiziert. Jedem Punkt auf der Kugel außer dem Nordpol entspricht dann eine komplexe Zahl. Durch Hinzunahme des Nordpols, der mit ∞ identifiziert wird, entsteht die Riemannsche Zahlenkugel. Die Metrik ist dann der Abstand zweier Punkte auf der Kugeloberfläche.
Eigenschaften
Sei f also eine meromorphe Funktion auf dem Abschluss der komplexen Zahlen, also der Quotient zweier teilerfremden Polynome. Zudem sei der Grad von f größer als Eins. Der Grad einer meromorphen Funktion ist das Maximum der teilerfremden Polynome in Zähler und Nenner. Der Grad gibt im allgemeinen an, wie viele Urbilder ein Punkt besitzt. Je nachdem, welche Dynamik der Prozess
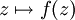 für einen bestimmten Startwert zeigt, wird dieser Wert einer von zwei Mengen zugeordnet:
für einen bestimmten Startwert zeigt, wird dieser Wert einer von zwei Mengen zugeordnet:- Fatou-Menge
- Die Startwerte aus dieser Menge führen unter Iteration zu einer "stetigen" Dynamik, das heißt wenn sich der Startwert nur ein klein wenig ändert, dann zeigt auch die Dynamik ein ähnliches Verhalten
- Julia-Menge
- Die Punkte in dieser Menge führen zu "instabilen" Prozessen: Jede noch so kleine Änderung des Startwertes führt zu einer komplett anderen Dynamik.
Die Zahlenkugel ist die disjunkte Vereinigung dieser beiden Mengen. Jeder Punkt gehört also entweder zur Fatou-Menge oder zur Julia-Menge. Die Julia-Menge einer Funktion wird als Jf bezeichnet und die Fatou-Menge als Ff.
Die historische Definition der Julia-Menge, wie sie von Fatou und Julia stammt und unten nachzulesen ist, ist weder sonderlich intuitiv noch anschaulich. Daher werden hier einige Eigenschaften[2] dieser Mengen zusammengestellt, wozu zunächst ein paar grundlegende Begriffe gebraucht werden.
Begriffe
Für jeden Wert
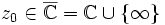 definiert die Rekursion
definiert die Rekursioneine Folge von Punkten auf der Riemannschen Zahlenkugel. Diese Folge wird auch als Orbit von z0 bezeichnet:
fn bedeutet dabei immer n-malige Hintereinanderausführung von f und ist nicht mit der n-ten Potenz zu verwechseln. Die Definition des inversen Orbits erfolgt etwas anders, weil f im Allgemeinen nicht eindeutig umkehrbar ist. Der inverse Orbit eines Punktes z0 besteht aus allen Punkten, die irgendwann auf diesen abgebildet werden:
Falls für ein n gilt zn = z0, dann heißt z0 ein periodischer Punkt und der Orbit
heißt periodischer Orbit oder Zyklus. Ist n die kleinste natürliche Zahl mit dieser Eigenschaft, dann heißt n die Periode des Zyklus. Falls dies für n = 1 zutrifft, also wenn f(z0) = z0 gilt, dann ist z0 ein Fixpunkt von f. Offenbar ist ein periodischer Punkt von f, dessen Periode gleich n ist, ein Fixpunkt von fn. Anhand der Ableitung kann man die Stabilität eines periodischen Punktes charakterisieren. Sei dazu
Dann heißt der periodische Punkt
- stark anziehend, wenn λ = 0
- anziehend, wenn 0 < | λ | < 1
- indifferent, wenn | λ | = 1
- abstoßend, wenn | λ | > 1
Durch Anwendung der Kettenregel sieht man, dass (fn)' für alle Punkte des Zyklusses den gleichen Wert hat, und analog heißt dieser Zyklus dann (stark) anziehend, indifferent oder abstoßend.
Diese Namensgebung ist durch folgende Beobachtung motiviert: Für den Fall
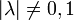 verhält sich fn in einer Umgebung des Fixpunktes z0 genauso wie g(z) = λz in einer Umgebung von Null. Unter Iteration wandern daher Werte immer näher an den Fixpunkt heran, wenn | λ | < 1 gilt, und für | λ | > 1 entfernen sich die Werte immer weiter vom Fixpunkt. Unter der Iteration zieht der Fixpunkt also Werte in seiner Umgebung an oder er stößt sie ab. Für | λ | = 1 ist der Fall komplizierter, und für λ = 0 werden die Werte mindestens so stark angezogen, wie von
verhält sich fn in einer Umgebung des Fixpunktes z0 genauso wie g(z) = λz in einer Umgebung von Null. Unter Iteration wandern daher Werte immer näher an den Fixpunkt heran, wenn | λ | < 1 gilt, und für | λ | > 1 entfernen sich die Werte immer weiter vom Fixpunkt. Unter der Iteration zieht der Fixpunkt also Werte in seiner Umgebung an oder er stößt sie ab. Für | λ | = 1 ist der Fall komplizierter, und für λ = 0 werden die Werte mindestens so stark angezogen, wie von 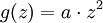 in einer Umgebung von 0.
in einer Umgebung von 0.Ist z0 ein anziehender Fixpunkt von f, dann heißt die Menge
das Einzugsgebiet des Fixpunktes. Die Menge A(z0) besteht also aus allen Punkten, deren Orbit gegen z0 konvergiert. Offenbar enthält diese Menge den inversen Orbit von z0. Das A kommt vom englischen basin of attraction (Einzugsgebiet/Sammelbecken des Attraktors, hier also Sammelbecken eines anziehenden Fixpunktes oder Zyklusses). Wenn γ ein anziehender periodischer Zyklus der Periode n ist, dann hat jeder der Fixpunkte
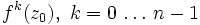 sein Einzugsgebiet, und A(γ) bezeichnet die Vereinigung dieser Einzugsgebiete.
sein Einzugsgebiet, und A(γ) bezeichnet die Vereinigung dieser Einzugsgebiete.Definition
Eine mögliche Definition der Julia-Menge geschieht über die Menge ihrer abstoßenden periodischen Punkte:
wobei Abschluss den topologischen Abschluss meint.
Jedes Element der Julia-Menge lässt sich also als Grenzwert einer konvergenten Folge darstellen, die nur aus abstoßenden periodischen Punkten von f besteht.
Grundlegende Eigenschaften
Einige Eigenschaften der Julia-Menge sind:
-
- Die Menge der abstoßenden periodischen Punkte ist dicht in Jf
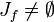 und enthält überabzählbar viele Punkte
und enthält überabzählbar viele Punkte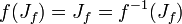
- Die Julia-Mengen von f und
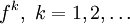 sind identisch
sind identisch - Für jedes z aus Jf ist der inverse Orbit
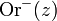 dicht in Jf
dicht in Jf - Ist γ ein anziehender Zyklus von f, dann gilt für das Einzugsgebiet des Zuklusses und dessen Rand:
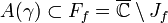 und
und 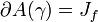
- Sei z ein Element der Julia-Menge und U eine Umgebung von z. Dann gibt es eine natürliche Zahl n = n(U) mit
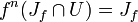
- Falls die Julia-Menge innere Punkte hat, dann gilt
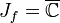
Erläuterungen
-
- Dies folgt direkt aus der gegebenen Definition
- Jede rationale Funktion hat einen beachtlichen Vorrat an abstoßenden periodischen Punkten
- Die Julia-Mengen ist invariant unter f: wendet man f punktweise auf die Julia-Menge an, ist das Ergebnis wieder die Julia-Menge. Gleiches gilt für die Menge der Urbilder.
- Folgt durch Induktion aus dem vorherigen Punkt
- Dieser Punkt inspiriert zu einem Verfahren zur Visualisierung der Julia-Menge durch Rückwärts-Iteration. Allerdings sind die Urbilder nicht gleichverteilt in Jf und die Urbilder im Allgemeinen nicht einfach zu bestimmen
- Diese Eigenschaft ist für ein bildgebendes Verfahren einsetzbar, wenn man einen anziehenden Zyklus kennt. Liegt ein Punkt im Einzugsgebiet dieses Zyklus, färbt man ihn zum Beispiel weiß, ansonsten schwarz. Die Julia-Menge ist dann die Grenze zwischen den beiden Gebieten. Außerdem sagt diese Eigenschaft, dass die Julia-Menge in vielen Fällen fraktale Eigenschaften haben muss. Hat die Funktion f z.B: mehr als zwei anziehende Fixpunkte a, b, c, ... dann gilt
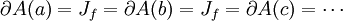
das heißt jeder Punkt der Julia-Menge liegt auf dem Rand jedes Einzugsgebietes. Und alle Einzugsgebiete haben denselben Rand. - Aus einem beliebig kleinen Stück lässt dich die Julia-Menge rekonstruieren, in dem man die Funktion f endlich oft (punktweise) darauf anwendet. Zudem besitzt die Julia-Menge keine isolierten Punkte.
Kritische Punkte
Ein Punkt z heißt kritischer Punkt von f, wenn f in keiner Umgebung von z umkehrbar ist. Ist f differenzierbar, dann ist ein kritischer Punkt durch
charakterisiert. In jedem Einzugsgebiet, das zu einem (stark) anziehenden Attraktor gehört, liegt mindestens ein kritischer Punkt. Indem man die kritischen Punkte einer Funktion betrachtet, können daher Aussagen über die Dynamik dieser Funktion getroffen werden.
Ein bekanntes Beispiel dafür ist die Mandelbrotmenge, deren Bezug zu bestimmten Julia-Mengen weiter unten erläutert wird. Die Mandelbrotmenge kartographiert die unterschiedlichen Verhalten des kritischen Punktes 0 der Abbildung z→z²+c für verschiedene Werte von c.
Julia-Mengen von Polynomen
Eine einfache Art, die Julia-Menge eines Polynoms p zu definieren, ist folgende Rekursion:
- zn+1 = p(zn)
mit einem Startwert z0.
Die Menge Kp definiert man als die Menge aller komplexer Zahlen z0, deren Betrag nach beliebig vielen Iterationsschritten beschränkt bleibt. Die Julia-Menge Jp ist dann der Rand dieser Menge. Kp wird als ausgefüllte Julia-Menge oder gelegentlich auch unpräzise als Julia-Menge selbst bezeichnet. Man kann nachweisen, dass Kp beschränkt ist.
Diese Definition ist die direkte Umsetzung der Eigenschaft 6: Für ein Polynom ist ∞ ein anziehender Fixpunkt. Die Julia-Menge ergibt sich also als Rand des Einzugsgebietes dieses Fixpunkts. Falls ein Punkt darin liegt, dann konvergiert er schließlich gegen ∞ oder – bei Verwendung der Standardmetrik – wächst sein Betrag über alle Grenzen. Bleibt sein Betrag beschränkt, dann gehört er zum Einzugsgebiet eines anderen Attraktors oder zur Julia-Menge selbst.
Dieses "Definition" wird in der Regel zur Erzeugung von Grafiken verwendet, da sie leicht in ein Computerprogramm übersetzt werden kann.
Für meromorphe Funktionen, deren Zählergrad um mindestens 2 größer ist als ihr Nennergrad, kann man die gleiche Definition verwenden, da auch für solche Funktionen ∞ ein anziehender Fixpunkt ist.
Dynamik am Beispiel z→z2
An diesem einfachen Beispiel lassen sich schon viele Eigenschaften der Julia-Menge nachweisen.
Die Funktion f(z) = z2 hat drei Fixpunkte: 0, 1 und ∞. Für diese Punkte gilt f(z) = z. Da die Ableitung in 0 und in ∞ verschwindet, sind diese beiden Fixpunkte anziehende Fixpunkte, während 1 abstoßend ist. Alle Startwerte, deren Betrag kleiner als 1 ist, konvergieren gegen 0, und alle Startwerte, deren Betrag größer als 1 ist, konvergieren gegen ∞:
Im verbleibenden Fall | z | = 1 liegt z auf dem Einheitskreis und hat die Darstellung
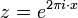 , und es ist
, und es ist 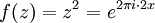 . Anwendung von f verdoppelt also lediglich den (reellen) Exponenten in der Polarkoordinatendarstellung, der Betrag der Zahl bleibt immer gleich 1. Der Exponent x kann immer so gewählt werden, dass er im halboffenen Intervall [0,1) liegt. Betrachtet man nur die Wirkung von f auf die Variable x im Exponenten, dann entspricht f der Abbildung
. Anwendung von f verdoppelt also lediglich den (reellen) Exponenten in der Polarkoordinatendarstellung, der Betrag der Zahl bleibt immer gleich 1. Der Exponent x kann immer so gewählt werden, dass er im halboffenen Intervall [0,1) liegt. Betrachtet man nur die Wirkung von f auf die Variable x im Exponenten, dann entspricht f der Abbildungauf dem Intervall [0,1) der reellen Zahlen, das heißt einer Multiplikation mit 2 wobei nur die Nachkommastellen relevant sind. Der Fixpunkt 1 von f wird zum Fixpunkt 0 von g. Iteriert man den Wert 1/3 mit g, dann ergibt sich die Folge
Also ist 1/3 ein periodischer Punkt, ebenso 2/3. In der Darstellung einer Zahl als Dualbruch werden durch die Multiplikation mit 2 nur die Ziffern um eine Stelle nach links geschoben, und die Vorkommastelle wird durch das mod immer auf 0 gesetzt, wie im Beispiel 3/8 zu sehen:
Betrachtet man die Mengen
dann sieht man direkt, dass P die Menge der periodischen Punkte von g ist, weil die Nachkommastellen der Elemente von P periodisch sind. Die Menge der periodischen Punkte – dies sind die rationalen Zahlen mit ungeradem Nenner – liegen dicht im Intervall [0,1). Mit der obigen Definition entspricht das Intervall der Julia-Menge von f. Die Julia-Menge von f ist also der Rand des Einheitskreises S1:
Alle Elemente von W werden schließlich auf Null abgebildet, denn die Elemente von W haben eine abbrechende Dualentwicklung. W ist also der inverse Orbit von 0 unter g. Gemäß Eigenschaft 5 ist diese Menge dicht in der Julia-Menge: die Zahlen mit abbrechender Dualentwicklung sind dicht im Intervall [0,1). Die Julia-Menge ist sowohl der Rand des Einzugsgebietes von ∞ als auch der Rand des Einzugsgebietes von Null (Eigenschaft 6).
Eigenschaft 7 lässt sich auch direkt nachweisen: Sei U eine Umgebung eines Punktes von Jf, das heißt ein Teilstück des Einheitskreises der Länge
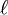 . Ist die Länge kleiner als der Halbkreis, dann verdoppelt sich die Länge des Teilstücks mit jeder Anwendung von f. Man wähle das n daher so, dass
. Ist die Länge kleiner als der Halbkreis, dann verdoppelt sich die Länge des Teilstücks mit jeder Anwendung von f. Man wähle das n daher so, dass 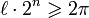 gilt und hat die komplette Julia-Menge überdeckt.
gilt und hat die komplette Julia-Menge überdeckt.Alle rationalen Zahlen führen zu Folgen, die schließlich periodisch werden. Grund dafür ist, dass rationale Zahlen eine periodische Dualentwicklung haben. Entsprechend führen irrationale Zahlen zu Folgen, die nicht periodisch werden.
Dynamik quadratischer Polynome
Im allgemeinen Fall quadratischer Polynome genügt es, Polynome der Gestalt
zu betrachten, denn alle anderen quadratischen Polynome lassen sich durch eine lineare Koordinatentransformation in diese Darstellung bringen.
Ebenso wie bei der Normalparabel ist ∞ ein anziehender Fixpunkt der Abbildung, und in einer Umgebung von ∞ gibt es eine Transformation
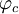 , welche fc in eine Normalparabel überführt:
, welche fc in eine Normalparabel überführt:Liegt ein Punkt zn in dieser Umgebung und ist fc dort umkehrbar, dann lässt sich zu dem Punkt mittels der Iterationsvorschrift das Urbild zn−1 finden:
Das Urbild wird so ausgewählt, dass die Transformation
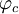 stetig auf den neuen, größeren Bereich fortgesetzt werden kann. Durch dieses Verfahren kann die Umgebung, in der fc die gleiche Dynamik hat wie z2, sukzessive vergrößert werden — zumindest so lange, wie die Funktion umkehrbar ist, also man durch Rückwärtsiteration nicht zu einem kritischen Punkt der Funktion gelangt. Entscheidend für die Dynamik ist daher das Verhalten des kritischen Punktes 0. Dies ist der einzige kritische Punkt außer ∞.
stetig auf den neuen, größeren Bereich fortgesetzt werden kann. Durch dieses Verfahren kann die Umgebung, in der fc die gleiche Dynamik hat wie z2, sukzessive vergrößert werden — zumindest so lange, wie die Funktion umkehrbar ist, also man durch Rückwärtsiteration nicht zu einem kritischen Punkt der Funktion gelangt. Entscheidend für die Dynamik ist daher das Verhalten des kritischen Punktes 0. Dies ist der einzige kritische Punkt außer ∞.Liegt 0 im Einzugsbereich von ∞, dann kann die Transformation irgendwann nicht mehr weitergeführt werden, weil die Rückwärtsiteration zu diesem Punkt der Nicht-Umkehrbarkeit von fc gelangt. Falls der Punkt 0 nicht gegen ∞ strebt, dann kann der Homöomorphismus
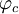 für alle Punkte außerhalb der Kreisscheibe ausgedehnt werden. In diesem Fall ist die Julia-Menge von fc zusammenhängend.
für alle Punkte außerhalb der Kreisscheibe ausgedehnt werden. In diesem Fall ist die Julia-Menge von fc zusammenhängend.Liegt 0 hingegen im Einzugsgebiet von ∞, dann kann die Transformation nicht bis zur Kreisscheibe ausgedehnt werden, weil man zu einem Verzweigungspunkt, nämlich dem kritischen Punkt, gelangt. In diesem Fall kann es neben dem Attraktor ∞ keinen anderen anziehenden Attraktor geben, denn jeder anziehende Attraktor enthält mindestens einen kritischen Punkt. In diesem Fall besteht die Julia-Menge aus Cantor-Staub und die Fatou-Menge hat nur eine einzige Zusammenhangskomponente.
Beziehung zur Mandelbrot-Menge
Diese beiden grundlegend verschiedenen Eigenschaften geben Anlass zur Definition einer Parametermenge, welche alle komplexen Zahlen beinhaltet, für welche der kritische Punkt 0 von fc nicht nach ∞ entweicht: die Mandelbrot-Menge
Das heißt die Mandelbrot-Menge ist die Menge der Parameter c, für welche die Rekursion zn+1 = zn2 + c beschränkt bleibt, wenn man z0 = 0 wählt.
Die Mandelbrotmenge ist also eine Beschreibungsmenge der Julia-Mengen quadratischer Polynome. Jedem Punkt c der komplexen Zahlenebene entspricht eine Julia-Menge. Eigenschaften der Julia-Menge lassen sich an der Lage von c relativ zur Mandelbrot-Menge beurteilen: Wenn der Punkt c Element der Mandelbrot-Menge ist, dann sind sowohl die Julia-Menge Jc als auch Kc zusammenhängend. Andernfalls sind beide Cantormengen unzusammenhängender Punkte. Liegt der Punkt in M, dann besteht die Fatou-Menge aus zwei Zusammenhangskomponeten, nämlich aus dem von der Julia-Menge umgrenzten Gebiet sowie dem Einzugsgebiet von ∞. Liegt c nicht in der Mandelbrot-Menge, dann besteht die Fatou-Menge nur aus dem Einzugsgebiet von ∞.
Falls c in der Nähe des Randes der Mandelbrotmenge liegt, dann ähnelt die entsprechende Julia-Menge den Strukturen der Mandelbrot-Menge in der näheren Umgebung von c.
Graphische Darstellung der Julia-Mengen
Zur graphischen Darstellungen der ausgefüllten Julia-Mengen Kc in der zweidimensionalen komplexen Zahlenebene wird die Farbe eines Punktes danach gewählt, wie viele Iterationen notwendig waren, bis
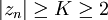 , da die Iteration für alle z mit
, da die Iteration für alle z mit 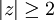 divergiert. Punkte, die nach einer vorgegebenen Maximalzahl von Iterationsschritten betragsmäßig kleiner als K sind, werden als konvergierend angenommen und in der Regel schwarz dargestellt. Die Wahl von K=2 ist zwar möglich, allerdings ergeben sich für größere Werte wie K=1000 harmonischere Färbungen, die zudem gut den Äquipotentiallinien einer elektrisch aufgeladenen Julia-Menge entsprechen.
divergiert. Punkte, die nach einer vorgegebenen Maximalzahl von Iterationsschritten betragsmäßig kleiner als K sind, werden als konvergierend angenommen und in der Regel schwarz dargestellt. Die Wahl von K=2 ist zwar möglich, allerdings ergeben sich für größere Werte wie K=1000 harmonischere Färbungen, die zudem gut den Äquipotentiallinien einer elektrisch aufgeladenen Julia-Menge entsprechen.Die allgemeine Definition
Für holomorphe oder meromorphe Funktionen f, die keine Polynome sind, kann obiges Verfahren nicht angewendet werden, da die iterierten Funktionswerte im Allgemeinen für keinen einzigen Anfangswert gegen Unendlich laufen. Es gibt mehrere Möglichkeiten, die Julia-Menge J(f)für solche allgemeinen Funktionen zu definieren:
- J(f) ist dann die kleinste unendliche und abgeschlossene Teilmenge der komplexen Ebene, die invariant unter f ist, d.h. deren Bild und Urbild wieder ganz in der Menge enthalten ist. Beispielsweise ist für jedes Polynom p(z) vom Grad ≥ 2 über den komplexen Zahlen der Rand der Menge { z | Die Folge
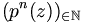 ist beschränkt} abgeschlossen, unendlich groß und invariant unter p(z). Deswegen muss er die Julia-Menge von p(z) enthalten. Dass der Rand in der Tat gleich der Julia-Menge ist, verlangt allerdings noch einige Arbeit.
ist beschränkt} abgeschlossen, unendlich groß und invariant unter p(z). Deswegen muss er die Julia-Menge von p(z) enthalten. Dass der Rand in der Tat gleich der Julia-Menge ist, verlangt allerdings noch einige Arbeit. - J(f) ist die Menge der Punkte, bei denen die Familie der iterierten Funktionen (f)n nicht gleichgradig stetig auf jeder kompakten Teilmenge von J(f) ist. Konkret: Gibt es zu gegebenem
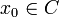 ein ε > 0, so dass in jeder noch so kleinen Umgebung um x0 ein Punkt z liegt, für den die iterierten Werte fn(z0) und fn(z) irgendwann einen Abstand großer ε haben, so gehört z0 zur Julia-Menge von f. Hierbei darf man allerdings die komplexe Zahlenebene nicht mit der euklidischen Metrik versehen. Vielmehr muss man die komplexen Zahlen als Riemannsche Zahlenkugel auffassen und mit der entsprechenden sphärischen Metrik versehen.
ein ε > 0, so dass in jeder noch so kleinen Umgebung um x0 ein Punkt z liegt, für den die iterierten Werte fn(z0) und fn(z) irgendwann einen Abstand großer ε haben, so gehört z0 zur Julia-Menge von f. Hierbei darf man allerdings die komplexe Zahlenebene nicht mit der euklidischen Metrik versehen. Vielmehr muss man die komplexen Zahlen als Riemannsche Zahlenkugel auffassen und mit der entsprechenden sphärischen Metrik versehen.
Allerdings lautet die historische Definition nach Julia und Fatou:
- Sei f eine rationale (oder meromorphe) Funktion auf der Riemannschen Zahlenkugel
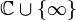 . Dann heißt ein Punkt
. Dann heißt ein Punkt 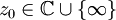 normaler Punkt von f, falls die Familie der Iterierten
normaler Punkt von f, falls die Familie der Iterierten 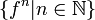 in einer offenen Umgebung des Punktes z0 eine normale Familie ist. Die Menge aller normalen Punkte bezeichnen wir als Fatou-Menge F(f) und ihr Komplement
in einer offenen Umgebung des Punktes z0 eine normale Familie ist. Die Menge aller normalen Punkte bezeichnen wir als Fatou-Menge F(f) und ihr Komplement 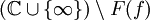 bezeichnen wir als Julia-Menge J(f) von f.
bezeichnen wir als Julia-Menge J(f) von f.
Verallgemeinerung
Man kann auch die ursprüngliche Definition auf die Algebra der Quaternionen ausweiten. Diese ist ein reell vierdimensionaler Raum, weshalb eine vollständige Darstellung einer Juliamenge darin problematisch ist. Es ist aber möglich, den Schnitt einer solchen Julia-Menge mit einer dreidimensionalen Hyperebene zu visualisieren.
Bildgebung
Siehe auch
Literatur
- Alan F. Beardon: Iteration of rational functions. Springer, 1991.
- Christoph Dötsch: Dynamik meromorpher Funktionen auf der Riemannschen Zahlenkugel. Diplomica GmbH Hamburg, 2008.
Weblinks
- Dynamik meromorpher Funktionen auf der Riemannschen Zahlenkugel - Zur Charakterisierung von Julia - Mengen (PDF) (Christoph Dötsch, 2008)
- Julia-Fraktale erforschen (Java-Plugin erforderlich)
Einzelnachweise
Wikimedia Foundation.