- K-partiter Graph
-
Ein k-partiter Graph ist in der Graphentheorie ein einfacher Graph, dessen Knotenmenge in k disjunkte Teilmengen zerfällt, sodass die Knoten jeder dieser Teilmengen untereinander nicht benachbart sind. Für k = 2 heißen diese Graphen bipartite Graphen.
Jeder k-partite Graph ist auch immer ein k+x-partiter Graph, wobei x eine natürliche Zahl und k+x kleiner als die Knotenzahl ist.
Definitionen
Ein Graph G=(V,E) heißt k-partit, falls
 eine Partition von V ist und
eine Partition von V ist und .
.
Man beachte, dass die Partition nicht eindeutig ist. Es ist durchaus möglich, dass es mehrere Partitionen gibt, die diese Eigenschaft erfüllen.
Man nennt den Graphen dann vollständig k-partit, falls außerdem jeder Knoten mit allen Knoten aller anderen Partitionen verbunden ist, wenn also gilt:
 .
.
Mit
 notiert man einen vollständig k-partiten Graphen, mit | Vi | = ni.
notiert man einen vollständig k-partiten Graphen, mit | Vi | = ni.Beispiel Turán-Graph
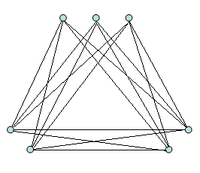
Die Turán-Graphen Tm(n) (
 ) sind vollständige m-partite Graphen. Das nebenstehende Beispiel T3(7) ist 3-partit. Bezeichnet
) sind vollständige m-partite Graphen. Das nebenstehende Beispiel T3(7) ist 3-partit. Bezeichnet  die Floor-Funktion, so ist
die Floor-Funktion, so ist .
.Für das nebenstehende Beispiel gilt damit
T3(7) = K2,2,3.
Kategorie:- Graphenklasse
Wikimedia Foundation.