Satz von Turán

Der Satz von Turán (nach Pál Turán) ist eine Aussage aus dem mathematischen Teilgebiet der Graphentheorie. Er macht eine Aussage über die maximale Anzahl von Kanten, die ein Graph mit gegebener Knotenzahl haben kann, ohne einen vollständigen Untergraphen mit m Knoten enthalten zu müssen.

Der Fall der Dreiecke

Es sei G ein ungerichteter Graph mit n Knoten. Ein Untergraph aus drei Knoten heißt in naheliegender Weise ein Dreieck, wenn je zwei dieser drei Knoten durch eine Kante verbunden sind. Der Satz von Turán präzisiert die Aussage, dass der Graph, wenn er keine Dreiecke enthalten soll, nicht zu viele Kanten haben kann:

• Satz von Turán (Dreiecke)^[1]: Hat ein Graph G mit n Knoten keine Dreiecke, so hat er höchstens $\left\lfloor \frac{n^2}{4} \right\rfloor$ Kanten.

Dabei ist $\lfloor x \rfloor$ die größte ganze Zahl, die kleiner gleich x ist.

Für kleine n ist die Aussage klar:

Graphen mit 4 Knoten und mindestens 5 Kanten enthalten mindestens ein Dreieck.

• n = 1: Dieser Graph hat weder Kanten noch Dreiecke und es ist $\left\lfloor \frac{1^2}{4} \right\rfloor = 0$.
• n = 2: Solche Graphen haben keine Dreiecke und höchstens eine Kante; es ist $\left\lfloor \frac{2^2}{4} \right\rfloor = 1$.
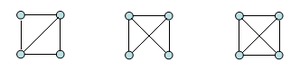
• n = 3: Solche Graphen haben genau dann ein Dreieck, wenn die Kantenzahl 3 ist; und es ist $\left\lfloor \frac{3^2}{4} \right\rfloor = 2$.
• n = 4: Es ist $\left\lfloor \frac{4^2}{4} \right\rfloor = 4$ und tatsächlich hat jeder 4er-Graph mit 5 Kanten mindestens ein Dreieck.

Für größere n führt man die Aussage auf Graphen mit n − 2 Knoten zurück, was dann einen Induktionsbeweis ermöglicht, wobei man gerade und ungerade n unterscheiden muss. Hier soll nur der Fall für gerade n kurz angedeutet werden:

Entfernt man a und b aus G so verbleiben nur die schwarzen Kanten.

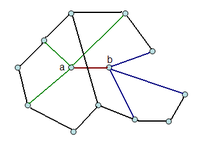
Man entferne eine Kante, die zwei Knoten a und b verbindet, aus G. Der so erhaltene Untergraph enthält ebenfalls keine Dreiecke und nur n − 2 Knoten, also gemäß Induktionsvoraussetzung höchstens $\left\lfloor \frac{(n-2)^2}{4}\right\rfloor = \frac{(n-2)^2}{4}$ Kanten. Der Graph G hat darüber hinaus noch die entfernte Kante und weitere Kanten, die von a oder b ausgehen und in $G\setminus\{a,b\}$ enden. Gehen etwa k von a aus, so müssen die von b ausgehenden Kanten in anderen Knoten von $G\setminus \{a,b\}$ enden, denn anderenfalls enthielte G ein Dreieck, das heißt von b können höchstens n − 2 − k Kanten in $G\setminus \{a,b\}$ endende ausgehen. Die maximal mögliche Kantenzahl von G ist daher $\frac{(n-2)^2}{4}+1+k+(n-2-k) \,=\, \frac{n^{2}-4n+4}{4} + 1 + n - 2 \,=\, \frac{n^2}{4} - n +1 + 1 + n - 2 \,=\, \frac{n^2}{4}$. Daraus folgt die Behauptung für gerade n. Der Fall ungerader n kann ganz ähnlich behandelt werden.

Die durch den Satz von Turán angegebene Grenze ist scharf, wie das Beispiel des bipartiten Graphen K_n,n zeigt, denn dieser Graph hat 2n Knoten und $n^2 = \frac{(2n)^2}{4}$ Kanten.

Der Turán-Graph

Ein Dreieck ist der vollständige Graph K₃. Es stellt sich daher die Frage, ob man eine Obergrenze für die Anzahl von Kanten eines Graphen, der keinen zu K_m isomorphen Untergraphen enthält, angeben kann. Um diese Frage beantworten zu können, wird der so genannte Turán-Graph wie folgt definiert:

Der Turán-Graph T₃(7)

Der Turán-Graph T_m(n) ist der vollständige m-partite Graph, der in der k-ten Klasse $\lfloor \frac{n+k-1}{m} \rfloor$ Elemente hat. Beachte dazu, dass

$\lfloor \frac{n}{m}\rfloor + \lfloor \frac{n+1}{m}\rfloor + \ldots + \lfloor \frac{n+m-1}{m}\rfloor = n$

gilt und T_m(n) daher n Knoten hat. Die Anzahl der Kanten von T_m(n) werde mit t_m(n) bezeichnet. Man kann zeigen, dass

$t_m(n) = \frac{(m-1)(n^2-r^2)}{2m} + \frac{r(r-1)}{2}$

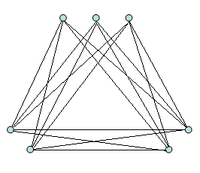
wobei $r \equiv n \,\mathrm{mod} \,m,\,\, 0 \le r < m$ ist und mod für die Division mit Rest steht.

Der nebenstehende Turán-Graph T₃(7) hat demnach $\frac{(3-1)(49-1)}{2\cdot 3} + \frac{1\cdot(1-1)}{2} = \frac {2\cdot 48}{6} = 16$ Kanten.

Eine leichte Rechnung zeigt $t_m(n) = \frac{n^2}{2}(1-\frac{1}{m} +\frac{r^2}{mn^2}-\frac{r}{n^2}) \le \frac{n^2}{2}(1-\frac{1}{m})$. Diese obere Abschätzung der Kantenzahl des Turán-Graphen wird häufig verwendet.

Der allgemeine Fall

• Satz von Turán^[2]: Hat ein Graph G mit n Knoten keinen zu K_m isomorphen Untergraphen ($m \ge 3$), so hat er höchstens t_{m − 1}(n) Kanten. Jeder Graph ohne einen zu K_m isomorphen Untergraphen mit n Knoten und t_{m − 1}(n) Kanten ist isomorph zum Turán-Graphen T_{m − 1}(n).

In der extremalen Graphentheorie definiert man zu einem Graphen H die Zahl ex(n,H) als die maximale Kantenzahl, die ein Graph mit n Knoten und ohne einen zu H isomorphen Untergraphen haben kann. Der Satz von Turán hat daher folgendes Korollar:

$\mathrm{ex}(n,K_m) \,=\, t_{m-1}(n) \le \frac{n^2}{2}\cdot(1-\frac{1}{m-1})$

Der Satz von Turán sagt aber mehr aus, nämlich dass je zwei Graphen mit n Knoten ohne einen zu K_m isomorphen Untergraphen, die diesen Extremwert realisieren, isomorph zu T_{m − 1}(n) sind.

Ist m = 3 und n gerade, so ist $0 \equiv n \,\mathrm{mod}\, 2$ und daher $t_2(n) = \frac{(2-1)(n^2-0^2)}{2\cdot 2} + 0 = \frac{n^2}{4}$. Ist n ungerade, so ist $1 \equiv n \,\mathrm{mod}\, 2$ und daher $t_2(n) = \frac{(2-1)(n^2-1^2)}{2\cdot 2} + 0 = \frac{n^2-1}{4} = \lfloor \frac{n^2}{4}\rfloor$. Daher ist $\mathrm{ex}(n,K_3) \,=\, \lfloor \frac{n^2}{4} \rfloor$ und man erhält den bereits oben besprochenen Spezialfall der Dreiecke.

Die im Satz vorgenommene Einschränkung $m\ge 3$ kann zu $m\ge 2$ abgeschwächt werden, auch wenn der dadurch entstehende Fall nicht sonderlich interessant ist. Ein Graph ohne einen zu K₂ isomorphen Untergraphen ist ein kantenloser Graph und tatsächlich ist t₁(n) = 0 für alle n. Auch die Fälle $m \ge n$ müssen nicht ausgeschlossen werden. Für m = n ist r = 1 in der oben für t_m(n) angegebenen Formel, und es ist daher $t_{n-1}(n) = \frac{(n-2)(n^2-1)}{2(n-1)}+0 = \frac{(n-2)(n+1)}{2} = \frac{n(n-1)}{2} - 1$; man erhält daher die triviale Aussage, dass ein Graph mit n Knoten genau dann einen zu K_n isomorphen Untergraphen enthält, wenn er vollständig ist, denn K_n hat $\frac{n(n-1)}{2}$ Kanten. Ist m = n + 1, so ist r = 0 und daher $t_m(n) = \frac{n(n-1)}{2}$, ist m > n + 1 so ist r = n und daher ebenfalls $t_{m-1}(n) = \frac{r(r-1)}{2} = \frac{n(n-1)}{2}$; das heißt, in den Fällen m > n kann der Graph so viele Kanten wie möglich haben, was klar ist, da er ohnehin keinen zu K_m isomorphen Untergraphen enthalten kann.

Einzelnachweise

1. ↑ Frank Harary: Graphentheorie. R. Oldenburg, München 1974, ISBN 3-486-34191-X.
2. ↑ Béla Bollobás: Graph Theory, An Introductory Course, Springer Verlag New York (1979), ISBN 0-387-90399-2, IV, §2, Theorem 6

Literatur

• K. Wagner: Graphentheorie, Bibliographisches Institut AG, Mannheim (1970), ISBN 3-411-00248-4
• P. Turan: Eine Extremalaufgabe aus der Graphentheorie, Mat. Fiz. Lapok. 48 (1941), Seiten 436-452 (Ungarisch)