Einfacher Graph

Einfacher Graph

In der Graphentheorie ist ein einfacher Graph (auch schlichter Graph) ein ungerichteter Graph ohne Mehrfachkanten und ohne Schleifen.

Ein einfacher Graph ist also ein geordnetes Paar (V,E), wobei V eine endliche Menge von Knoten und E eine Menge von Kanten ist. Die Menge E ist dabei Teilmenge der 2-elementigen Teilmengen von V, das heißt, jede Kante ist eine Menge von zwei Knoten. Ein einfacher Graph mit n Knoten kann demzufolge maximal {n \choose 2} = \frac{n (n-1)}{2} Kanten haben. Sind sie alle vorhanden, wird er der vollständige Graph Kn genannt.

Weitere Begriffe und Verallgemeinerungen werden im Artikel Typen von Graphen in der Graphentheorie erklärt.

Beispiel

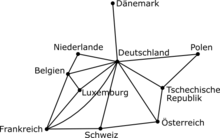
Beispielgraph: Deutschland und Nachbarländer

Die Nachbarschaftsbeziehungen zwischen Deutschland und seinen Nachbarländern können als einfacher Graph modelliert werden. In diesem Beispiel umfasst die Menge V die Länder und jede Kante steht dafür, dass zwei Länder benachbart sind. In der nebenstehenden Abbildung wird dieser Graph dargestellt, wobei die Knoten als Punkte und die Kanten als Verbindungslinien gezeichnet sind. Man beachte, dass der Graph nur die bestehenden Beziehungen umfasst, dagegen sind Position und Größe der Knoten und Kanten frei gewählt.

Wenn die Kanten zusätzlich mit Werten versehen sind (z.B. Entfernungen), spricht man von einer Gewichtung (auch Bewertung) der Kanten und des Graphen.

Literatur


Wikimedia Foundation.

Игры ⚽ Нужен реферат?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Graph mit Mehrfachkanten — Ein Graph besteht in der Graphentheorie anschaulich aus einer Menge von Punkten, zwischen denen Linien verlaufen. Die Punkte nennt man Knoten oder Ecken, die Linien nennt man meist Kanten, manchmal auch Bögen. Auf die Form der Knoten und Kanten… …   Deutsch Wikipedia

  • Graph ohne Mehrfachkanten — Ein Graph besteht in der Graphentheorie anschaulich aus einer Menge von Punkten, zwischen denen Linien verlaufen. Die Punkte nennt man Knoten oder Ecken, die Linien nennt man meist Kanten, manchmal auch Bögen. Auf die Form der Knoten und Kanten… …   Deutsch Wikipedia

  • Bogen (Graph) — Dieses Stichwortverzeichnis enthält kurze Definitionen und Erklärungen zu den wichtigsten graphentheoretischen Begriffen. A Abstand Siehe: Distanz. Achromatische Zahl Die achromatische Zahl ψ(G) eines Graphen G ist die größte Zahl k, für die G… …   Deutsch Wikipedia

  • K-regulärer Graph — Dieses Stichwortverzeichnis enthält kurze Definitionen und Erklärungen zu den wichtigsten graphentheoretischen Begriffen. A Abstand Siehe: Distanz. Achromatische Zahl Die achromatische Zahl ψ(G) eines Graphen G ist die größte Zahl k, für die G… …   Deutsch Wikipedia

  • Kubischer Graph — Dieses Stichwortverzeichnis enthält kurze Definitionen und Erklärungen zu den wichtigsten graphentheoretischen Begriffen. A Abstand Siehe: Distanz. Achromatische Zahl Die achromatische Zahl ψ(G) eines Graphen G ist die größte Zahl k, für die G… …   Deutsch Wikipedia

  • Metrischer Graph — Dieses Stichwortverzeichnis enthält kurze Definitionen und Erklärungen zu den wichtigsten graphentheoretischen Begriffen. A Abstand Siehe: Distanz. Achromatische Zahl Die achromatische Zahl ψ(G) eines Graphen G ist die größte Zahl k, für die G… …   Deutsch Wikipedia

  • Regulärer Graph — Dieses Stichwortverzeichnis enthält kurze Definitionen und Erklärungen zu den wichtigsten graphentheoretischen Begriffen. A Abstand Siehe: Distanz. Achromatische Zahl Die achromatische Zahl ψ(G) eines Graphen G ist die größte Zahl k, für die G… …   Deutsch Wikipedia

  • Schleifenfreier Graph — Dieses Stichwortverzeichnis enthält kurze Definitionen und Erklärungen zu den wichtigsten graphentheoretischen Begriffen. A Abstand Siehe: Distanz. Achromatische Zahl Die achromatische Zahl ψ(G) eines Graphen G ist die größte Zahl k, für die G… …   Deutsch Wikipedia

  • Schleifenloser Graph — Dieses Stichwortverzeichnis enthält kurze Definitionen und Erklärungen zu den wichtigsten graphentheoretischen Begriffen. A Abstand Siehe: Distanz. Achromatische Zahl Die achromatische Zahl ψ(G) eines Graphen G ist die größte Zahl k, für die G… …   Deutsch Wikipedia

  • Ungerichteter Graph — Dieses Stichwortverzeichnis enthält kurze Definitionen und Erklärungen zu den wichtigsten graphentheoretischen Begriffen. A Abstand Siehe: Distanz. Achromatische Zahl Die achromatische Zahl ψ(G) eines Graphen G ist die größte Zahl k, für die G… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”