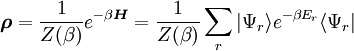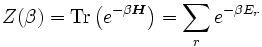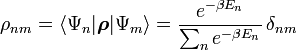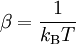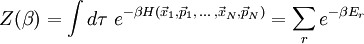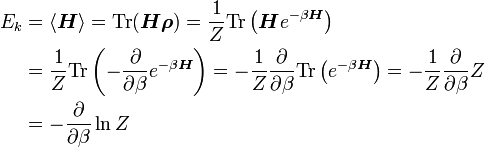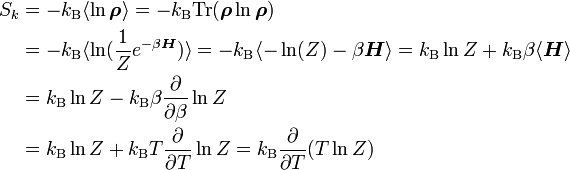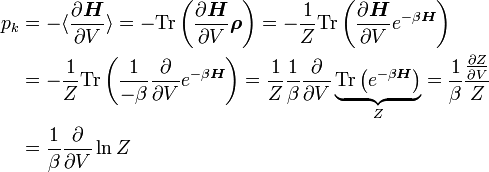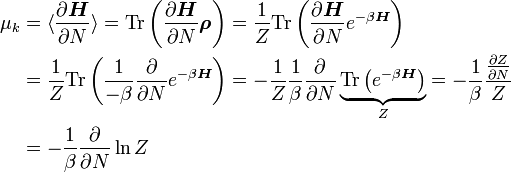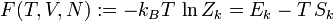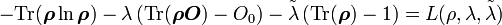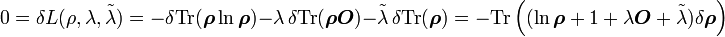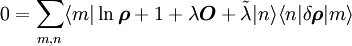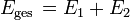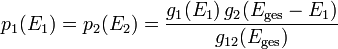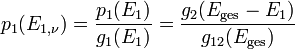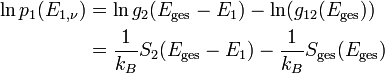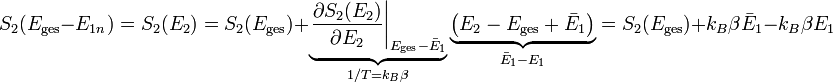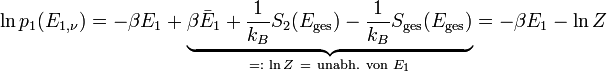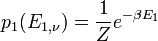Kanonischer Zustand

Das kanonische Ensemble ist in der statistischen Physik ein System mit festgelegter Teilchenzahl in einem konstanten Volumen, das Energie mit einem Reservoir austauschen kann und mit diesem im thermischen Gleichgewicht ist. Dies entspricht einem System mit vorgegebener Temperatur, wie ein geschlossenes System (kein Teilchenaustausch) in einem Wärmebad (makroskopisches System, das sehr viel größer ist als das betrachtete System).

Ein solches Ensemble wird durch einen kanonischen Zustand ρ beschrieben. Dies ist der Gleichgewichtszustand, dessen statistische Entropie S(ρ), unter Berücksichtigung der Nebenbedingung $\langle \boldsymbol{H}\rangle=\textrm{Tr}(\boldsymbol{\rho H})=E$ (der Energieerwartungswert ist festgelegt), nach der Maximum-Entropie-Methode maximal ist, wobei der Zustand mit von außen vorgegebenen Parametern, wie Volumen und Teilchenzahl, verträglich sein muss.

Quantenmechanisch

Der Dichteoperator des kanonischen Zustands ist festgelegt durch

$\boldsymbol{\rho}=\frac{1}{Z(\beta)}e^{-\beta\boldsymbol{H}}=\frac{1}{Z(\beta)}\sum_{r}|\Psi_{r}\rangle e^{-\beta E_{r}}\langle\Psi_{r}|$

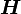wobei die $|\Psi_{r}\rangle$ die zu $\boldsymbol{H}$ gehörenden Energieeigenzustände zur Energie E_r sind und die kanonischen Zustandssumme durch

$Z(\beta)=\textrm{Tr}\left(e^{-\beta\boldsymbol{H}}\right)=\sum_{r}e^{-\beta E_{r}}$

gegeben ist.

Die Spur eines Operators ist folgendermaßen definiert: 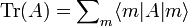$\textrm{Tr}(A)=\sum\nolimits_{m}\langle m|A|m\rangle$ für beliebiges vollständiges Orthonormalsystem $\left\{ |m\rangle\right\}$.

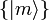In der Energieeigenbasis ist die zugehörige Dichtematrix diagonal

$\rho_{nm}=\langle\Psi_{n}|\boldsymbol{\rho}|\Psi_{m}\rangle=\frac{e^{-\beta E_{n}}}{\sum_{n}e^{-\beta E_{n}}}\,\delta_{nm}$

Der Parameter β kann als inverse Temperatur aufgefasst werden

$\beta=\frac{1}{k_{{\rm B}}T}$

Klassisch

Analog ergibt sich der klassische kanonische Zustand (Phasenraumdichte)

$\rho=\frac{1}{Z(\beta)}e^{-\beta H(\vec{x}_{1},\vec{p}_{1},\,...\,,\vec{x}_{N},\vec{p}_{N})}=\frac{1}{Z(\beta)}e^{-\beta E_{r}}$

mit der klassischen kanonischen Zustandssumme

$Z(\beta)=\int d\tau\; e^{-\beta H(\vec{x}_{1},\vec{p}_{1},\,...\,,\vec{x}_{N},\vec{p}_{N})}=\sum_{r}e^{-\beta E_{r}}$

mit $d\tau =\frac{1}{\xi} \frac{1}{(2\pi\hbar)^{3N}}\;d^3x_1d^3p_1\,...\,d^3x_Nd^3p_N$

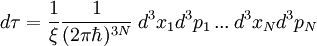
wobei für N identische Teilchen der Faktor ξ = N! die Mehrfachzählung ununterscheidbarer Teilchen verhindert,

und für n verschiedene Teilchensorten mit N₁,...,N_n Teilchenzahlen und 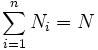$\sum^{n}_{i=1}N_i=N$ der Faktor $\xi=N_1!\,...\,N_n!$.

Erwartungswerte

Im Folgenden werden Erwartungswerte verschiedener makroskopischer Größen gebildet. Der Index k bedeutet kanonisch. Der Hamiltonoperator ist vom Volumen und der Teilchenzahl abhängig H(V,N), die Zustandssumme von Temperatur, Volumen und Teilchenzahl Z(T,V,N) bzw. Z(β,V,N).

Der Energieerwartungswert kann über die Zustandsumme berechnet werden

$\begin{align} E_{k} & =\langle\boldsymbol{H}\rangle = \textrm{Tr}(\boldsymbol{H\rho})=\frac{1}{Z}\textrm{Tr}\left(\boldsymbol{H}e^{-\beta\boldsymbol{H}}\right)\\ & = \frac{1}{Z}\textrm{Tr}\left(-\frac{\partial}{\partial\beta}e^{-\beta\boldsymbol{H}}\right) = -\frac{1}{Z}\frac{\partial}{\partial\beta}\textrm{Tr}\left(e^{-\beta\boldsymbol{H}}\right)=-\frac{1}{Z}\frac{\partial}{\partial\beta}Z\\ & = -\frac{\partial}{\partial\beta}\ln Z \end{align}$

Die statistische Entropie lässt sich nun durch die Zustandssumme ausdrücken

$\begin{align} S_{k} & =-k_{{\rm B}}\langle\ln\boldsymbol{\rho}\rangle= -k_{{\rm B}}\textrm{Tr}(\boldsymbol{\rho}\ln\boldsymbol{\rho})\\ & = -k_{{\rm B}}\langle\ln(\frac{1}{Z}e^{-\beta\boldsymbol{H}})\rangle=-k_{{\rm B}}\langle-\ln(Z)-\beta\boldsymbol{H}\rangle=k_{{\rm B}}\ln Z+k_{{\rm B}}\beta\langle\boldsymbol{H}\rangle\\ & = k_{{\rm B}}\ln Z-k_{{\rm B}}\beta\frac{\partial}{\partial\beta}\ln Z \\ & =k_{{\rm B}}\ln Z+k_{{\rm B}}T\frac{\partial}{\partial T}\ln Z=k_{{\rm B}}\frac{\partial}{\partial T}(T\ln Z) \end{align}$

Der Druckerwartungswert ist gleich:

$\begin{align} p_{k} & = -\langle\frac{\partial\boldsymbol{H}}{\partial V}\rangle=-\textrm{Tr}\left(\frac{\partial\boldsymbol{H}}{\partial V}\boldsymbol{\rho}\right)=-\frac{1}{Z}\textrm{Tr}\left(\frac{\partial\boldsymbol{H}}{\partial V}e^{-\beta\boldsymbol{H}}\right)\\ & = -\frac{1}{Z}\textrm{Tr}\left(\frac{1}{-\beta}\frac{\partial}{\partial V}e^{-\beta\boldsymbol{H}}\right)=\frac{1}{Z}\frac{1}{\beta}\frac{\partial}{\partial V}\underbrace{\textrm{Tr}\left(e^{-\beta\boldsymbol{H}}\right)}_{Z}=\frac{1}{\beta}\frac{\frac{\partial Z}{\partial V}}{Z}\\ & = \frac{1}{\beta}\frac{\partial}{\partial V}\ln Z \end{align}$

Für große Systeme lässt sich auch das chemische Potential berechnen (die Teilchenzahl N ist eine diskrete Größe; erst im thermodynamischen Limes lässt sich N quasi-kontinuierlich behandeln und Ableitungen nach N sind möglich):

$\begin{align} \mu_{k} & = \langle\frac{\partial\boldsymbol{H}}{\partial N}\rangle=\textrm{Tr}\left(\frac{\partial\boldsymbol{H}}{\partial N}\boldsymbol{\rho}\right)=\frac{1}{Z}\textrm{Tr}\left(\frac{\partial\boldsymbol{H}}{\partial N}e^{-\beta\boldsymbol{H}}\right)\\ & = \frac{1}{Z}\textrm{Tr}\left(\frac{1}{-\beta}\frac{\partial}{\partial N}e^{-\beta\boldsymbol{H}}\right)=-\frac{1}{Z}\frac{1}{\beta}\frac{\partial}{\partial N}\underbrace{\textrm{Tr}\left(e^{-\beta\boldsymbol{H}}\right)}_{Z}=-\frac{1}{\beta}\frac{\frac{\partial Z}{\partial N}}{Z}\\ & = -\frac{1}{\beta}\frac{\partial}{\partial N}\ln Z \end{align}$

Offensichtlich spielt bei der Berechnung von Erwartungswerten der Logarithmus der Zustandssumme ein wichtige Rolle. Deswegen definiert man die Freie Energie:

$F(\beta,V,N):=-\frac{1}{\beta}\ln Z_{k}=E_{k}-\frac{1}{k_{B}\beta}S_{k}$

$F(T,V,N):=-k_{B}T\,\ln Z_{k}=E_{k}-T\,S_{k}$

Die freie Energie ist das thermodynamische Potential des kanonischen Zustands. Obige Erwartungswerte lassen sich nun kompakt als Gradient des Potentials schreiben:

$\begin{pmatrix}-S_{k}\\ -p_{k}\\ \mu_{k}\end{pmatrix}=\begin{pmatrix}\partial_{T}\\ \partial_{V}\\ \partial_{N}\end{pmatrix}F(T,V,N)$

Herleitung des Gleichgewichtszustands bei festgelegtem Erwartungswert

Variationsproblem

Der Gleichgewichtszustand bei festgelegtem Erwartungswert(en) kann als Variationsproblem aufgefasst werden und mit der Methode der Lagrange-Multiplikatoren hergeleitet werden.

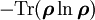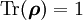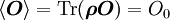Der Ausdruck $-\textrm{Tr}(\boldsymbol{\rho}\ln\boldsymbol{\rho})$ soll mit den Nebenbedingungen $\textrm{Tr}(\boldsymbol{\rho})=1$ und $\langle\boldsymbol{O}\rangle = \textrm{Tr}(\boldsymbol{\rho}\boldsymbol{O})=O_{0}$ maximiert werden. Sind mehrere Erwartungswerte festgelegt, so sind 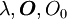$\lambda,\boldsymbol{O},O_0$ mehrkomponentige Größen

$-\textrm{Tr}(\boldsymbol{\rho}\ln\boldsymbol{\rho})-\lambda\left(\textrm{Tr}(\boldsymbol{\rho O})-O_{0}\right)-\tilde{\lambda}\left(\textrm{Tr}(\boldsymbol{\rho})-1\right)=L(\rho,\lambda,\tilde{\lambda})$

Die Variation von L liefert eine stationäre Lösung. Verwendet wird dabei die Relation $\delta\textrm{Tr}\left(f(\rho)\right)=\textrm{Tr}\left(f'(\rho)\,\delta \rho\right)$

$0=\delta L(\rho,\lambda,\tilde{\lambda})=-\delta\textrm{Tr}(\boldsymbol{\rho}\ln\boldsymbol{\rho})-\lambda\,\delta\textrm{Tr}(\boldsymbol{\rho O})-\tilde{\lambda}\,\delta\textrm{Tr}(\boldsymbol{\rho})=-\textrm{Tr}\left( (\ln\boldsymbol{\rho}+1+\lambda\boldsymbol{O}+\tilde{\lambda})\delta\boldsymbol{\rho}\right)$

$0=\sum_{m,n}\langle m|\ln\boldsymbol{\rho}+1+\lambda\boldsymbol{O}+\tilde{\lambda}|n\rangle\langle n|\delta\boldsymbol{\rho}|m\rangle$

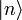wobei die $|m\rangle$ und $|n\rangle$ jeweils ein VONS bilden; die Summe über m beschreibt die Spurbildung, die Summe über n ist das Einschieben einer 1 (Ausnutzen der Vollständigkeit)

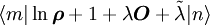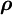
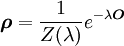Der Ausdruck ist für alle m,n gleich 0, wenn $\langle m|\ln\boldsymbol{\rho}+1+\lambda\boldsymbol{O}+\tilde{\lambda}|n\rangle$ gleich 0 ist. Daraus ergibt sich der Dichteoperator $\boldsymbol{\rho}$

$\boldsymbol{\rho}=\frac{1}{Z(\lambda)}e^{-\lambda\boldsymbol{O}}$    mit    $Z(\lambda)=e^{\tilde{\lambda}+1}$

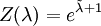
Die Definition eines Dichteoperators fordert, dass die Spur darüber 1 wird: 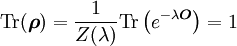$\textrm{Tr}(\boldsymbol{\rho})=\frac{1}{Z(\lambda)}\textrm{Tr}\left(e^{-\lambda\boldsymbol{O}}\right)=1$ daraus folgt der Boltzmann-Gibbs-Zustand

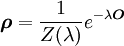$\boldsymbol{\rho}=\frac{1}{Z(\lambda)}e^{-\lambda\boldsymbol{O}}$    mit    $Z(\lambda)=\textrm{Tr}\left(e^{-\lambda\boldsymbol{O}}\right)$

Aus der Variationsrechnung folgt nur das stationäre Verhalten; das Maximum bezüglich der Entropie lässt sich mit der Gibbs-Ungleichung zeigen.

Ist 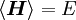$\langle\boldsymbol{H}\rangle=E$ die einzige Information über das System, so ergibt sich der oben dargestellte kanonische Zustand (ist 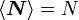$\langle\boldsymbol{N}\rangle=N$ eine weitere Nebenbedingung erhält man den großkanonischen Zustand).

Anschauliche Herleitung

Das Wärmebad (Index 2) und das interessierende System (Index 1) haben schwach-energetischen Kontakt. Sie bilden zusammen ein Gesamtsystem, das nach außen vollständig abgeschlossen ist und somit mikrokanonisch beschrieben werden muss. Die Gesamtenergie bleibt stets konstant:

$E_{\text{ges}\,}=E_{1}+E_{2}$

Die Energie E₂ = E_ges − E₁ des Wärmebads sei g₂(E₂)-fach entartet, die Energie E₁ des angekoppelten Systems sei g₁(E₁)-fach entartet. Der Entartungsgrad des Gesamtsystems zur Energie E_ges ist

$g_{12}(E_{\text{ges}})=\sum_{E_{1}^{\prime}=0}^{E_{\text{ges}}}g_{1}(E_{1}^{\prime})\, g_{2}(E_{\text{ges}}-E_{1}^{\prime})$.

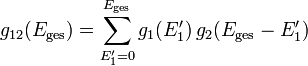Im mikrokanonischen Ensemble hat jeder mögliche Basiszustand dieselbe Wahrscheinlichkeit 1 / g₁₂(E_ges). Die Wahrscheinlichkeit p₁(E₁), dass das System 1 die Energie E₁ besitzt, ist gleich der Wahrscheinlichkeit p₂(E₂), dass das Wärmebad die Energie E_ges − E₁ hat; diese ist der Quotienten aus Gesamtentartungsgrad zur Energie E₁ des Systems 1, nämlich 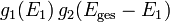$g_{1}(E_{1})\, g_{2}(E_{\text{ges}}-E_{1})$, und des Gesamtentartungsgrads g₁₂(E_ges):

$p_{1}(E_{1})=p_{2}(E_{2})=\frac{g_{1}(E_{1})\, g_{2}(E_{\text{ges}}-E_{1})}{g_{12}(E_{\text{ges}})}$

Die Wahrscheinlichkeit das System 1 in einem bestimmten Basiszustand (Quantenzahl ν) mit Energie E₁ zu finden ist:

$p_{1}(E_{1,\nu})=\frac{p_{1}(E_{1})}{g_{1}(E_{1})}=\frac{g_{2}(E_{\text{ges}}-E_{1})}{g_{12}(E_{\text{ges}})}$

Man logarithmiert und kann die Entropie des Wärmebades S₂ = k_Blng₂ und die Gesamtentropie S_ges = k_Blng₁₂ identifizieren:

$\begin{align} \ln p_{1}(E_{1,\nu}) & =\ln g_{2}(E_{\text{ges}}-E_{1})-\ln(g_{12}(E_{\text{ges}}))\\ & =\frac{1}{k_{B}}S_{2}(E_{\text{ges}}-E_{1})-\frac{1}{k_{B}}S_{\text{ges}}(E_{\text{ges}})\end{align}$

Da das Wärmebad viel größer als das angekoppelte System ist, entspricht die Gesamtenergie fast ausschließlich der Energie des Bades (minus einer vergleichsweise kleinen mittleren Energie des Systems 1) und man kann die Entropie S₂(E_ges − E_1n) in eine Taylorreihe um 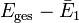$E_{\text{ges}}-\bar{E}_{1}$ bis zur ersten Ordnung entwickeln:

$S_{2}(E_{\text{ges}}-E_{1n})=S_{2}(E_{2})=S_{2}(E_{\text{ges}})+\underbrace{\left.\frac{\partial S_{2}(E_{2})}{\partial E_{2}}\right|_{E_{\text{ges}}-\bar{E}_{1}}}_{1/T=k_{B}\beta}\underbrace{\left(E_{2}-E_{\text{ges}}+\bar{E}_{1}\right)}_{\bar{E}_{1}-E_{1}}=S_{2}(E_{\text{ges}})+k_{B}\beta\bar{E}_{1}-k_{B}\beta E_{1}$

Dabei wurde ausgenutzt, dass die Ableitung der Entropie nach der Energie die inverse Temperatur ist. Dies setzt man in die logarithmierte Wahrscheinlichkeit ein. Außerdem werden noch die E₁-unabhängigen Terme als Konstante ( − lnZ) zusammengefasst

$\ln p_{1}(E_{1,\nu})=-\beta E_{1}+\underbrace{\beta\bar{E}_{1}+\frac{1}{k_{B}}S_{2}(E_{\text{ges}})-\frac{1}{k_{B}}S_{\text{ges}}(E_{\text{ges}})}_{=:\,\,\ln Z\ =\ \text{unabh. von }E_{1}}=-\beta E_{1}-\ln Z$

Exponenzieren liefert die Wahrscheinlichkeit, dass sich das System 1 im Basiszustand ν zur Energie E₁ befindet:

$p_{1}(E_{1,\nu})=\frac{1}{Z}e^{-\beta E_{1}}$

Die Konstante Z lässt sich über die Normierungsbedingung für Wahrscheinlichkeiten $\sum\nolimits_{n}p_{n}=1$ direkt aus den Eigenschaften des Systems 1 bestimmen (es muss eine minimale Energie geben; angenommen das Energiespektrum erstrecke sich bis $-\infty$, so würde die Summe divergieren):

$Z=\sum_{E_{1},\nu}e^{-\beta E_{1}}$

Da man normalerweise nur am System 1 interessiert ist, geht das System 2, das Wärmebad, nur über die Temperatur ein.

Literatur

• Balian: From Microphysics to Macrophysics 1. Springer-Verlag, Berlin, 2. Auflage 2006, ISBN 3-540-45469-1
• Schwabl: Statistische Mechanik. Springer-Verlag, Berlin, 3. Auflage 2006, ISBN 978-3-540-31095-2

Siehe auch

• Ensemble (Physik)
• Mikrokanonischer Zustand
• Zustandssumme