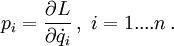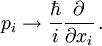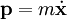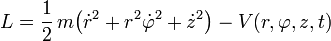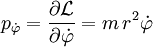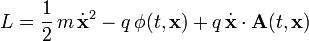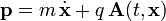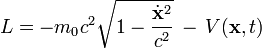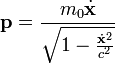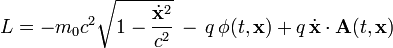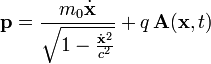Kanonischer Impuls

Der generalisierte Impuls (auch verallgemeinerter, kanonischer, kanonisch konjugierter oder konjugierter Impuls) tritt in der Hamiltonschen Mechanik auf. Zusammen mit dem Ort kennzeichnet er den jeweiligen Zustand des Systems, der sich mit der Zeit gemäß der Hamiltonschen Bewegungsgleichungen ändert.

Als Funktion des Ortes und der Geschwindigkeit ist der generalisierte Impuls die Ableitung der Lagrange-Funktion L nach der Geschwindigkeit $\dot q$

$p_{i}={\frac{{\partial L}}{{\partial \dot q_i }}}\,,\ i=1 .... n\,.$

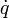
Beim Übergang von der klassischen Physik zur Quantenmechanik wird der kanonische Impuls (im Gegensatz zum kinetischen Impuls) mit dem Impulsoperator ersetzt,

$p_i\rightarrow\frac{\hbar}{i}\frac{\partial}{\partial x_i}\,.$

Beispiele

Klassische Bewegung

• Bei Bewegung eines Teilchens der Masse m in einem Potential 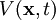$V(\mathbf{x},t)$ ohne Zwangsbedingungen in kartesischen Koordinaten

$L = \frac{1}{2}\, m\, \dot{\mathbf{x}}^2-V(\mathbf{x},t)$,

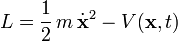ist der generalisierte Impuls gleich dem kinetischen Impuls

$\mathbf p = m \dot \mathbf x$

• Bei Bewegung eines Teilchens der Masse m in einem Potential $V(r,\varphi,z,t)$

$L = \frac 1 2\, m \bigl(\dot r^2 + r^2 \dot\varphi^2 + \dot z^2 \bigr)- V(r,\varphi,z,t)$

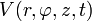
ist in Zylinderkoordinaten der zum Winkel konjugierte generalisierte Impuls die Komponente des Drehimpulses in Richtung der Zylinderachse.

$p_{\dot\varphi} = \frac{\partial \mathcal L}{\partial \dot \varphi}= m\,r^2\dot \varphi$

• Bei Bewegung einer Punktladung q mit Masse m im elektromagnetischen Feld

$L = \frac{1}{2}\, m\, \dot \mathbf x^2 - q\, \phi(t, \mathbf x) + q\, \dot \mathbf x\cdot \mathbf A(t, \mathbf x)$

hat der generalisierte Impuls zusätzlich zum kinetischen Impuls einen Beitrag vom Vektorpotential des Feldes

$\mathbf p = m\,\dot \mathbf x + q\, \mathbf A(t,\mathbf x)$

Relativistische Bewegung

• Bei der relativistischen Bewegung eines Teilchens der Ruhemasse m₀ in einem Potential 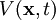$V(\mathbf{x},t)$ ohne Zwangsbedingungen in kartesischen Koordinaten

$L=-m_{0}c^{2}\sqrt{1-\frac{\dot{\mathbf{x}}^{2}}{c^{2}}}\,-\, V(\mathbf{x},t)$

ist der generalisierte Impuls gleich dem kinetischen Impuls

$\mathbf{p}=\frac{m_{0}\dot{\mathbf{x}}}{\sqrt{1-\frac{\dot{\mathbf{x}}^{2}}{c^{2}}}}$

• Bei relativistischer Bewegung einer Punktladung q mit Ruhemasse m₀ im elektromagnetischen Feld

$L = -m_{0}c^{2}\sqrt{1-\frac{\dot{\mathbf{x}}^{2}}{c^{2}}}\,-\, q\, \phi(t, \mathbf x) + q\, \dot \mathbf x\cdot \mathbf A(t, \mathbf x)$

hat der generalisierte Impuls zusätzlich zum kinetischen Impuls einen Beitrag vom Vektorpotential des Feldes

$\mathbf{p}=\frac{m_{0}\dot{\mathbf{x}}}{\sqrt{1-\frac{\dot{\mathbf{x}}^{2}}{c^{2}}}}+q\,\mathbf{A}(\mathbf{x},t)$