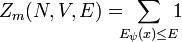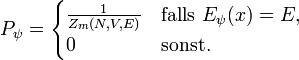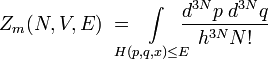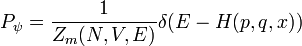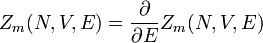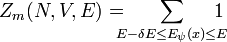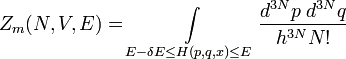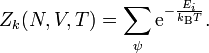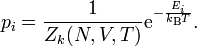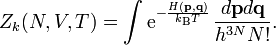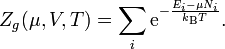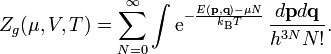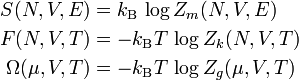Großkanonische Zustandssumme

Zustandssummen sind wesentliche Werkzeuge der statistischen Physik. Aus einer Zustandssumme (der Funktion, nicht dem Wert) lassen sich alle thermodynamischen Größen ableiten. Wenn die Teilchenzahlen N groß genug sind, kann man das System auch als kontinuierlich ansehen und die Zustandssummen als Zustandsintegrale formulieren.

Mikrokanonische Zustandssumme

Zunächst werden solche Systeme betrachtet, die sich in einem aus einer endlichen oder abzählbaren Zahl von Mikrozuständen (siehe auch: Mikrokanonischer Zustand) befinden können (Systeme mit überabzählbaren / kontinuierlichen Zuständen werden weiter unten diskutiert). Das zugehörige Ensemble heißt mikrokanonisches Ensemble. Dann ist die mikrokanonische Zustandssumme Z_m(E) gegeben durch die Zahl jener Mikrozustände ψ eines abgeschlossenen Systems im Gleichgewicht bei gegebener Energie E und festen äußeren Parametern N (Teilchenzahl) und V (Volumen), deren Gesamtenergie E_ψ(x) kleiner oder gleich E ist:

$Z_m(N,V,E) = \!\!\!\sum_{ E_{\psi} (x) \le E } \!\!\!1$

Die in der Mikrokanonik betrachteten abgeschlossenen Systeme haben eine konstante Energie. Befindet sich das System im Gleichgewicht (Entropie maximal) ist die Wahrscheinlichkeit, einen bestimmten Mikrozustand ψ anzutreffen:

$P_\psi = \begin{cases} \frac{1}{Z_m(N,V,E)} & \mbox{falls } E_\psi(x) = E,\\ 0 & \mbox{sonst.} \\ \end{cases}$

Hierbei ist Z_m(N,V,E) die Anzahl der Zustände mit Energie E.

In der klassischen Mechanik werden häufig Systeme betrachtet, deren Mikrozustand sich kontinuierlich ändern kann. Ein Beispiel ist das klassische Gas. Der Γ-Raum (auch Phasenraum genannt) eines klassischen Gases hat 6N Dimensionen: 3N Dimensionen für die Ortskoordinaten und 3N für die Impulskoordinaten der N Teilchen. Jeder Punkt (p,q) im Phasenraum entspricht einem Zustand ψ des Systems mit Energie E_ψ(x) = H(p,q,x), wobei H(p,q,x) die Hamiltonfunktion des Systems ist. Die in der Mikrokanonik betrachteten abgeschlossenen Systeme haben eine konstante Energie, die im Γ-Raum als Hyperfläche erscheint, auf der sich das System bewegen kann. Die Zustandssumme für ein solches Gas ist das von dieser H(p,q,x) = E-Hyperfläche umschlossene Volumen, welches sich als Zustandsintegral schreiben lässt: ^[1]

$Z_m(N,V,E) \;= \!\!\!\!\!\int\limits_{ H(p,q,x) \le E} \!\!\!\!\! \frac{d^{3N}p\; d^{3N} q}{h^{3N} N!}$

Die Wahrscheinlichkeit, das Gas in einem bestimmten Mikrozustand ψ anzutreffen, ist:

$P_\psi = \frac{1}{Z_m(N,V,E)} \delta(E - H(p,q,x) )$

mit

$Z_m(N,V,E) = \frac{\partial}{\partial E} Z_m(N,V,E)$

und der Dirac'schen δ-Funktion.

Oft findet man auch folgende abgewandelte Definition der mikrokanonische Zustandssumme. Summiert bzw. integriert wird dann über die Energieschale von E − δE bis E um die E = const-Hyperfläche des Systems im Γ-Raum. Die Schale hat dabei die Breite δE. Die diskrete Variante lautet:

$Z_m (N,V,E) = \!\!\!\!\sum_{ E - \delta E \le E_{\psi} (x) \le E } \!\!\!\!\!1$

Für kontinuierliche Systeme ist die Zustandssumme dann:

$Z_m(N,V,E) = \int\limits_{E - \delta E \le H(p,q,x) \le E} \frac{d^{3N}p\; d^{3N} q}{h^{3N} N!}$

In der Praxis ist jedoch die Integration über das gesamte umschlossene Volumen einfacher und führt für N > > 1 in sehr guter Näherung zum gleichen Ergebnis, da sich fast alle Zustände in der Randschale befinden.

Kanonische Zustandssumme

In der kanonischen Gesamtheit wird nicht die Energie des Systems vorgegeben, sondern die Temperatur. Diese Gesamtheit heißt auch Gibbs-Ensemble (siehe auch Kanonischer Zustand). Die Zustandssumme ist

$Z_k(N,V,T) = \sum_\psi\mathrm{e}^{-\frac{E_i}{k_\mathrm{B}T}}.$

Die Wahrscheinlichkeit eines Mikrozustandes i ist

$p_i = \frac{1}{Z_k(N,V,T)} \mathrm{e}^{-\frac{E_i}{k_\mathrm{B} T}}.$

Das kanonische Zustandsintegral ist ^[2]

$Z_k(N,V,T) = \int \mathrm{e}^{-\frac{H(\mathbf{p,q})}{k_\mathrm{B}T}} \, \frac{d\mathbf{p} d\mathbf{q}}{h^{3N} N!}.$

H ist die Hamilton-Funktion. Der Gibbs-Faktor 1 / N! stammt von der Ununterscheidbarkeit der Teilchen. Wenn man diesen Faktor wegließe, hätte man stattdessen N unterscheidbare Zustände und im Vergleich N! zu viele Mikrozustände.

Großkanonische Zustandssumme

In der großkanonischen Gesamtheit wird statt der Teilchenzahl N das chemische Potential μ vorgegeben. Die Wahrscheinlichkeit eines bestimmten Mikrozustandes i ist

$p_i = \frac{1}{Z_g(\mu, V, T)}\mathrm{e}^{-\frac{E_i - \mu N_i}{k_\mathrm{B} T}}$.

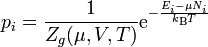Die Zustandssumme ist

$Z_g(\mu, V, T) = \sum_i\mathrm{e}^{-\frac{E_i - \mu N_i}{k_\mathrm{B}T}}.$

In integraler Schreibweise lautet die Zustandssumme bzw. das Zustandsintegral

$Z_g(\mu, V, T) = \sum\limits_{N=0}^{\infty} \int \mathrm{e}^{-\frac{E(\mathbf{p,q}) - \mu N}{k_\mathrm{B}T}} \, \frac{d\mathbf{p} d\mathbf{q}}{h^{3N} N!}.$

Man kann die großkanonische Zustandssumme aus der kanonischen Zustandssumme und der Fugazität z = exp(μ / k_BT) erhalten:

$Z_g(\mu, V, T) = \sum\limits_{N=0}^{\infty} Z_k(N,V,T) z^N = \sum_{N=0}^\infty Z_k(N,V,T)\,\mathrm{e}^{\frac{\mu N}{k_\mathrm{B}T}}$.

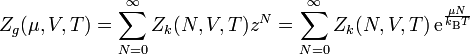Berechnung der thermodynamischen Potentiale

$\begin{align} S(N,V,E) &= k_\mathrm{B} \,\log Z_m(N,V,E)\\ F(N,V,T) &= - k_\mathrm{B}T \,\log Z_k(N,V,T)\\ \Omega(\mu, V, T) &= - k_\mathrm{B}T \,\log Z_g(\mu, V, T) \end{align}$

Hier ist S die Entropie, F die Freie Energie und Ω das großkanonische Potential.

Hinweis

Die englische Übersetzung von Zustandssumme ist partition function, nicht zu verwechseln mit Partitionsfunktion.

Referenzen

1. ↑ P. Hertz, Ann. Phys. (Leipzig) 33, 225 (1910). P. Hertz, Ann. Phys. (Leipzig) 33, 537 (1910).
2. ↑ Kanonisches Zustandsintegral

Literatur

• Richard Becker und Wolfgang Ludwig: Theorie der Wärme (Springer, Berlin, 1988), ISBN 3-540-15383-7
• Torsten Fließbach: Statistische Physik (1995), ISBN 3-86025-715-3 - Eine Einführung in die Statistische Physik und Thermodynamik

Siehe auch

• Ununterscheidbare Teilchen