- Kaufmännische Rundung
-
Rundung ist eine arithmetische Operation, bei der eine Zahl in Stellenschreibweise (meist eine Dezimalzahl) ersetzt wird durch eine Zahl mit einer geringeren Anzahl signifikanter (bedeutungstragender) Stellen. Dabei wird der Unterschied zwischen ursprünglicher und gerundeter Zahl (der Rundungsfehler) so gering wie möglich gehalten.
Inhaltsverzeichnis
Grundlagen
Zweck einer Rundung ist,
- Platz für die Darstellung zu sparen, insbesondere bei Dezimalbrüchen und Gleitkommazahlen, oder
- die Anzahl der Ziffern der Genauigkeit eines Rechenergebnisses anzupassen (siehe Fehlerrechnung).
Meist verringert man die Anzahl der Dezimalstellen und damit die Anzahl der dargestellten Ziffern. Doch werden auch große Ganzzahlen gerundet. Zum Beispiel rundet die Bundesagentur für Arbeit die errechnete Anzahl der Arbeitslosen auf volle 100. Hier bleibt die Anzahl der dargestellten Ziffern unverändert, aber die letzten zwei Stellen werden als nicht signifikant gekennzeichnet.
Wird eine positive Zahl vergrößert, so spricht man von Aufrunden, wird sie verkleinert, von Abrunden. Bei negativen Zahlen sind diese Wörter doppeldeutig. – Werden Nachkommastellen nur weggelassen, spricht man von Abschneiden.
Das Runden verändert in den meisten Fällen den Wert der gerundeten Zahl. Gängige Rundungsverfahren lassen sich gemäß der Richtung einteilen:
- aufwärts
- abwärts
- Richtung null
- zur nächstgelegenen Rundungszahl.
Kaufmännisches Runden
Das Kaufmännische Runden geschieht wie folgt:
- Ist die Ziffer an der ersten wegfallenden Dezimalstelle eine 0,1,2,3 oder 4, dann wird abgerundet.
- Ist die Ziffer an der ersten wegfallenden Dezimalstelle eine 5,6,7,8 oder 9, dann wird aufgerundet.
Diese Rundungsregel wird durch die Norm DIN 1333 beschrieben. Das Runden wird so auch häufig in der Schule gelehrt.
Beispiele (jeweils Rundung auf zwei Nachkommastellen)):
- 13,3749... € ≈ 13,37 €
- 13,3750... € ≈ 13,38 €
Negative Zahlen werden nach ihrem Betrag gerundet, bei einer 5 also weg von null:
- −13,3749... € ≈ −13,37 €
- −13,3750... € ≈ −13,38 €
Ist die Ausgangszahl jedoch ihrerseits das Ergebnis einer Rundung, so muss für den Grenzfall, dass alle bekannten Stellen nach der neuen Rundungsstelle Nullen sind, wenn möglich auf die exakte Zahl zurückgegriffen werden (etwa bei mathematischen Konstanten):
- exakte Zahl bekannt: 13,374999747…, gerundete Ausgangszahl: 13,3750
→ gerundete Zahl = 13,37 - exakte Zahl unbekannt, gerundete Ausgangszahl: 13,3750
→ gerundete Zahl = 13,38
In wissenschaftlichen Arbeiten und Logarithmentafeln wird manchmal kenntlich gemacht, ob die letzte Ziffer durch Auf- oder Abrunden erhalten wurde. Eine Ziffer, die durch Aufrunden erhalten wurde, wird mit einem Strich unter (oder auch oberhalb) der Ziffer kenntlich gemacht, eine Ziffer, die durch das Runden nicht verändert wurde (die Zahl wurde also abgerundet), wird mit einem Punkt über der Ziffer gekennzeichnet.
Beispiele:
- 3,4124928... wird zu
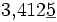 . Beim Runden auf drei Stellen nach dem Komma ist daher abzurunden.
. Beim Runden auf drei Stellen nach dem Komma ist daher abzurunden. - 2,6245241... wird zu
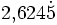 . Beim Runden auf drei Stellen nach dem Komma ist daher aufzurunden.
. Beim Runden auf drei Stellen nach dem Komma ist daher aufzurunden.
Sind keine weiteren Stellen bekannt, so wird die Ausgangszahl als exakt angenommen. Im Fall von Währungen wird das Ergebnis, ungeachtet des rein mathematischen Ergebnisses, auf fünf Stellen nach der Haupteinheit kaufmännisch gerundet und dann als exakt angesehen. So wurde der Umrechnungsfaktor von DM nach €,
1 € ≡ 1,95583 DM,
als exakt festgelegt.
Unverzerrte oder mathematische Rundung
Die Mathematische oder Unverzerrte Rundung ist wie folgt definiert:[1]
- Folgt auf die letzte beizubehaltende Ziffer eine 0, 1, 2, 3 oder 4, so wird abgerundet.
- Folgt auf die letzte beizubehaltende Ziffer eine 9, 8, 7, 6 oder eine 5, gefolgt von weiteren Ziffern, die nicht alle null sind, so wird aufgerundet.
- Folgt auf die letzte beizubehaltende Ziffer lediglich eine 5 (oder eine 5, auf die nur Nullen folgen), so wird derart gerundet, dass die letzte beizubehaltende Ziffer gerade wird.
Diese Art der Rundung wird in der Mathematik und Ingenieurswissenschaften verwendet. Sie ist im IEEE-754-Standard für das Rechnen mit binären Gleitkommazahlen in Computern vorgesehen. Weitere Namen für diese Art der Rundung sind Wissenschaftliches oder Symmetrisches Runden[2]; in englischsprachiger Literatur Round to Even oder Banker's Rounding[3].
Beispiele (Rundung auf eine Nachkommastelle):
- 2,2499 ≈ 2,2 (nach Regel 1)
- 2,2500 ≈ 2,2 (nach Regel 3 zur geraden Ziffer hin gerundet)
- 2,2501 ≈ 2,3 (nach Regel 2)
Kaufmännisches und unverzerrtes mathematisches Runden unterscheiden sich nur darin, wohin eine Zahl genau in der Mitte zwischen zwei Zahlen mit der gewählten Anzahl von Dezimalziffern gerundet wird.
Das kaufmännische Runden erzeugt kleine systematische Fehler, da das Aufrunden um 0,5 vorkommt, das Abrunden um 0,5 jedoch nie; das kann Statistiken geringfügig verzerren. Außerdem ist das Verhalten bei positiven und negativen Zahlen unterschiedlich, wenn die zu rundende Ziffer eine 5 ist.
Die mathematisch unverzerrte Rundung (englisch round to even) rundet von der genauen Mitte zwischen zwei Ziffern immer zur nächsten geraden Ziffer auf oder ab. Dadurch wird im Mittel genauso oft auf- wie abgerundet und der oben angesprochene systematische Fehler vermieden.
Summenerhaltendes Runden
Beim summenerhaltenden Runden werden die Teilbeträge so gerundet, dass die Summe der gerundeten Teilbeträge der Summe der ursprünglichen Beträge entspricht. Dieser Ansatz ist beispielsweise notwendig, wenn auf einer Rechnung zu jedem Posten einzeln die Mehrwertsteuerbeträge aufgeführt sind. Da die Summe der gerundeten Steuerbeträge der Einzelposten der Mehrwertsteuer aus der Summe der Nettobeträge entsprechen soll, ist hier summenerhaltendes Runden zwingend notwendig.
Eine mögliche Umsetzung ist das Mitführen des kumulierten Rundungsfehlers: Beim Runden der ersten Zahl entsteht ein Rundungsfehler. Der Rundungsfehler wird vor dem Runden der zweiten Zahl zu dieser addiert. Der neue Rundungsfehler ist dann die Differenz dieser Summe zu ihrem gerundeten Wert. Dieses Verfahren setzt man fort bis zur letzten Zahl. Der kumulierte Fehler liegt dabei immer im Intervall ( − 0,5;0,5). Das Verfahren ist einfach, aber statistisch betrachtet nicht optimal, da die erste Zahl anders behandelt wird als die folgenden. Andere Ansätze benutzen eine quadratische Ausgleichsrechnung um den Rundungsfehler auf die Teilbeträge zu verteilen.
Abrunden
Die Gaußklammer, auch Gauß-, Ganzzahl- oder Abrundungs-Funktion genannt, bildet jede reelle Zahl auf die größte ganze Zahl ab, die nicht größer ist als die reelle Zahl.
Folgerungen:
- Die Gaußfunktion ändert nicht das Vorzeichen, kann aber eine positive Zahl auf null abbilden.
- Für positive Zahlen in Stellenschreibweise ist die Anwendung der Gaußfunktion identisch mit dem Abschneiden der Nachkommastellen.
- Für jede negative nicht ganze Zahl ist der Betrag des Funktionswerts größer als der Betrag der Eingangszahl.
Rappenrundung
Eine Besonderheit in der Schweiz ist die Rappenrundung. Obwohl in der Schweiz durchaus nach Bedarf mit Rappen gerechnet wird, werden jedoch keine Beträge kleiner als 5 Rappen in Bargeld bezahlt oder in Rechnung gestellt. Effektive Geldbeträge müssen entsprechend gerundet werden. Sofern kaufmännisch gerundet wird, geschieht dies nach folgendem Schema:
Ausschlaggebend für die Rundung ist die Mitte zwischen 0 und 5 Rappen, resp. zwischen 5 und den nächsten 10 Rappen. Wenn die zu rundende Zahl gleich oder höher als die Mitte ist, wird aufgerundet, ansonsten abgerundet.
Beispiel:
- 1,000–1,024 → 1,00
- 1,025–1,074 → 1,05
- 1,075–1,099 → 1,10
Soll nicht kaufmännisch gerundet, sondern grundsätzlich abgerundet werden, geschieht dies nach dem folgenden Schema:
Beispiel:
- 1,000–1,049 → 1,00
- 1,050–1,099 → 1,05
- 1,100–1,149 → 1,10
Für die Berechnung der kaufmännischen Rappenrundung muss der zu rundende Betrag mal 20 gerechnet werden. Anschließend wird dieses Resultat auf 0 Stellen kaufmännisch gerundet. Am Ende wird der gerundete Betrag wieder durch 20 geteilt.
Rechnen mit gerundeten Zahlen
Werden gerundete Zahlen in eine Berechnung einbezogen, muss das Endergebnis auf die gleiche Anzahl signifikanter Stellen gerundet werden. Wenn z. B. eine Kraft mit 12,2 Newton gemessen wird, dann müssen alle Endergebnisse, die von dieser Kraft abhängen, so gerundet werden, dass maximal drei signifikante Stellen übrig bleiben. So wird dem Leser nicht eine höhere Genauigkeit vorgetäuscht, als wirklich vorhanden ist.
Rundung im Computer
Da Gleitkommazahlen im Computer nur einen bestimmten, endlichen Speicherbereich belegen, ist die Genauigkeit von Natur aus eingeschränkt. Nach mathematischen Operationen (wie der Multiplikation) entstehen zudem in der Regel Zahlen, die eine höhere Genauigkeit benötigen würden. Um das Ergebnis dennoch darstellen zu können, muss in irgendeiner Weise so gerundet werden, dass die Zahl in das vorgesehene Zahlenformat (z. B. IEEE 754) passt.
Das einfachste Rundungsschema ist das Abschneiden (engl. truncation oder chopping): Eine Zahl wird links eines bestimmten Punktes stehen gelassen, der Rest fallen gelassen. Dadurch wird sie auf die nächstmögliche Zahl abgerundet. Zum Beispiel wird, wenn man auf null Nachkommastellen rundet, aus 10,112 = 2,7510 eine 102 = 210. Diese Methode ist sehr schnell, sie leidet aber unter einem verhältnismäßig großen Rundungsfehler (im Beispiel beträgt er 0,7510).
Als weiteres Rundungsschema wird ebenfalls das kaufmännische Runden verwendet (engl. round-to-nearest). Man addiert dabei vor dem Runden 0,12 = 0,510 auf die zu rundende Zahl und schneidet danach ab. Im Beispiel hieße das, dass 2,75 + 0,5 = 3,25 abgeschnitten wird zu 3. Der Fehler beträgt hierbei nur 0,25. Allerdings ist dieses Runden positiv verzerrt.
Daher zieht man das mathematische Runden in Betracht (engl. round-to-nearest-even), das bei Zahlen x,510 = x,12 jeweils zur nächsten geraden Zahl rundet. Dieses Rundungsverfahren ist im IEEE-754-Standard vorgesehen. Alternativ kann auch auf die nächste ungerade Zahl gerundet werden (engl. round-to-nearest-odd).
Wenngleich das mathematische Runden eine gute numerische Leistung zeigt, benötigt es doch eine vollständige Addition, da das Übertragsbit im schlimmsten Fall durch alle Stellen der Zahl wandert. Damit besitzt es eine verhältnismäßig schlechte Laufzeitleistung. Als mögliche Umgehung dieser Problematik bietet sich eine vorgefertigte Tabelle an, die die gerundeten Ergebnisse enthält, welche nur noch abgerufen werden müssen.
Einzelnachweise
- ↑ Bronstein: Taschenbuch der Mathematik
- ↑ Didaktik der Zahlbereiche – Universität Augsburg, Prof. Dr. C. Bescherer
- ↑ How To Implement Custom Rounding Procedures – Article 196652, Microsoft Support (2004)
Weblinks
- Die Einführung des Euro und die Rundung von Währungsbeträgen – Europäische Kommission (1999)
Wikimedia Foundation.
