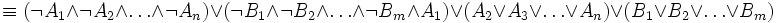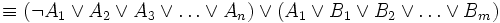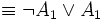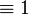- Klauselresolution
-
Die Resolution ist ein Verfahren der , um eine logische auf Gültigkeit zu testen.
Das Resolutionsverfahren, auch Resolutionskalkül genannt, ist ein : Statt direkt die einer Formel zu zeigen, leitet es einen logischen Widerspruch aus deren Verneinung ab.
Diese Herleitung geschieht mittels eines auf rein formalem Weg und kann deshalb von einem Computerprogramm durchgeführt werden. Die Resolution ist eine der bekanntesten Techniken des .
Inhaltsverzeichnis
Das Resolutionsverfahren in der Aussagenlogik
Resolvente (auch: Resolvent)
Seien C1, C2 einer Formel, die in vorliegt. Gibt es ein L, welches in C1 positiv und in C2 negativ vorkommt, ist die Vereinigung beider Klauseln ohne das positive und negative Literal L eine Resolvente (auch: der Resolvent)CR. Das heißt insbesondere: Gibt es kein komplementäres Literal, so gibt es auch keine Resolvente (
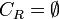 ).
).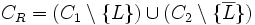
Es darf immer nur genau ein Literal resolviert werden. Je nach Ausgangsklauseln ist die Bildung verschiedener Resolventen möglich.
Anders notiert: Aus
wird auf die Resolvente
geschlossen.
Die Resolvente ist nicht äquivalent zu den Ausgangsklauseln. Die Bedeutung der Resolvente liegt vielmehr darin, dass die Ausgangsklauseln nur dann beide gleichzeitig erfüllbar sind, wenn auch die Resolvente erfüllbar ist (). Gelingt es die leere Klausel zu resolvieren, die stets unerfüllbar ist, ist somit die Unerfüllbarkeit der gesamten Formel gezeigt.
Beweis
Da die Resolvente CR eine für die Ausgangsklauseln C1 und C2 ist, gilt
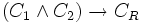 .
.
Man sagt CR folgt aus C1 und C2. Hieraus folgt der Beweis zur Korrektheit der Resolution:
Res-Operator
Das Ausführen eines einzelnen Resolutionsschrittes wird mit dem Res-Operator notiert:
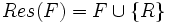 , wobei R eine Resolvente zweier Klauseln aus F ist
, wobei R eine Resolvente zweier Klauseln aus F ist
Mit
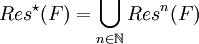 bezeichnet man die Vereinigung aller möglichen Resolutionsschritte auf F.
bezeichnet man die Vereinigung aller möglichen Resolutionsschritte auf F.Somit sind folgende Aussagen möglich:
- ist die leere Klausel Element von
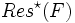 , ist F unerfüllbar und
, ist F unerfüllbar und - ist die leere Klausel Element von
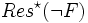 , ist F eine
, ist F eine
Resolution und Prädikatenlogik
Problemstellung
Für interessantere Problemstellungen ist das Instrumentarium der Aussagenlogik nicht ausreichend. Das Prinzip der Resolution sollte von der einfachen Aussagenlogik auf die erster Stufe ausgeweitet werden können. Neben logischen Literalen sind dabei zu berücksichtigen:
- Variablen (beispielsweise Zahlenvariablen), üblicherweise mit Symbolen wie x und y bezeichnet
- die Quantoren
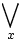 (es existiert ein x, für das gilt ...) und
(es existiert ein x, für das gilt ...) und 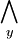 (für alle y gilt ...),
(für alle y gilt ...), - Konstanten, beispielsweise
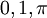
- ein- und mehrwertige , üblicherweise mit Symbolen wie f(x) oder g(x,y) bezeichnet.
Ein durchaus typisches Beispiel für eine prädikatenlogische Aussage ist:
1) 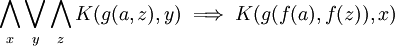
(Anmerkung: Setzen wir
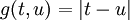 und
und 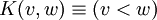 , so liefert uns die obige Formel die formal-logische Definition der der Funktion
, so liefert uns die obige Formel die formal-logische Definition der der Funktion 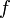 im Punkt
im Punkt 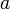 .)
.)Damit auf solche Aussagen die Resolution angewendet werden kann, müssen sie umgeformt und das oben beschriebene Verfahren erweitert werden.
Normalisierung
Die ersten Schritte bestehen darin, die zu widerlegende Aussage in eine Form zu bringen, die der konjunktiven Normalform der Aussagenlogik ähnelt.
- Man bringt die zu widerlegende Formel in die . Nach dieser Umformung stehen die Quantoren alle am Anfang der Formel, und der Rest der Formel hat die Gestalt einer konjunktiven Normalform.
- Durch die Anwendung von Skolemfunktionen eliminiert man alle Existenzquantoren
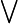 aus der Formel und bringt sie in die .
aus der Formel und bringt sie in die . - Nun sind alle Variablen in der Funktion an Allquantoren
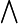 gebunden. Trifft man die Übereinkunft, Konstanten und Variablen unterschiedlich zu bezeichnen, beispielsweise Konstanten mit
gebunden. Trifft man die Übereinkunft, Konstanten und Variablen unterschiedlich zu bezeichnen, beispielsweise Konstanten mit 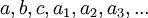 und Variablen mit
und Variablen mit 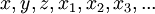 , dann kann auch auf die explizite Notation des Allquantors verzichtet werden. Man lässt ihn ebenfalls weg und erhält die der Aussage.
, dann kann auch auf die explizite Notation des Allquantors verzichtet werden. Man lässt ihn ebenfalls weg und erhält die der Aussage.
Beispielsweise lautet die Klauselform der Formel 1) aus dem vorigen Abschnitt:
2) 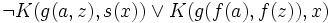
Substitution und Vereinheitlichung
Die Formeln
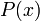
und 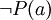
scheinen auf den ersten Blick nicht resolvierbar zu sein, da sie sich in
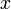 und
und 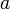 unterscheiden. Da die freie Variable
unterscheiden. Da die freie Variable 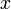 jedoch implizit ein Stellvertreter für alle
jedoch implizit ein Stellvertreter für alle 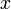 ist, darf (unter anderem)
ist, darf (unter anderem) 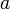 für
für 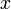 eingesetzt werden.
eingesetzt werden.Man erhält also die beiden Terme
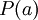
und 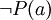
die sich offensichtlich miteinander resolvieren lassen.
Folgende Ersetzungen sind möglich:
3a) Ersetze Variable durch Konstante: 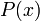

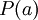
3b) Ersetze Variable durch eine andere Variable: 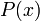

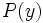
3c) Ersetze Variable durch Funktion einer Variablen: 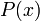

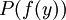
Die Ersetzung von Variablen in einem Literal muss in konsistenter Weise durchgeführt werden: Wird eine Variable an einer Stelle durch einen Term ersetzt, so muss dies innerhalb des Literals überall geschehen:
4a) Korrekte Ersetzung: 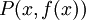

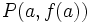
4b) Verbotene Ersetzung: 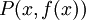
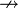
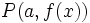
Sei
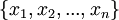 eine Menge von Variablen. Sei
eine Menge von Variablen. Sei 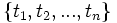 eine Menge von Termen, die aus Funktionen, Variablen oder Konstanten zusammengesetzt sein können.
eine Menge von Termen, die aus Funktionen, Variablen oder Konstanten zusammengesetzt sein können.- Ein System
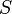 von Ersetzungen
von Ersetzungen 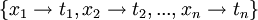 heißt eine Substitution.
heißt eine Substitution.
Seien
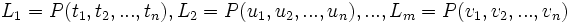 Literale über demselben Prädikat
Literale über demselben Prädikat 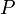 , wobei die
, wobei die 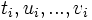 wiederum Terme sind.
wiederum Terme sind.- Eine Substitution
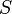 heißt eine Vereinheitlichung (oder auch Unifikator) von
heißt eine Vereinheitlichung (oder auch Unifikator) von 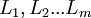 , wenn durch die Anwendung von
, wenn durch die Anwendung von 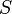 die Argumente aller Literale zur Übereinstimmung gebracht werden, das heißt, wenn
die Argumente aller Literale zur Übereinstimmung gebracht werden, das heißt, wenn 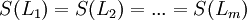 .
.
Zwei Literale über demselben Prädikat haben nicht notwendigerweise eine Vereinheitlichung. Beispielsweise lassen sich
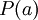 und
und 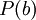 nicht vereinheitlichen, wenn
nicht vereinheitlichen, wenn 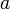 und
und 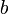 unterschiedliche Konstanten sind.
unterschiedliche Konstanten sind.- Eine Vereinheitlichung
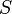 von Literalen heißt allgemeinste Vereinheitlichung, wenn es für jede andere Vereinheitlichung dieser Literale eine Substitution
von Literalen heißt allgemeinste Vereinheitlichung, wenn es für jede andere Vereinheitlichung dieser Literale eine Substitution 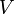 gibt, so dass
gibt, so dass 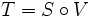 .
.
Wenn eine Menge von Literalen eine Vereinheitlichung besitzt, dann besitzt sie eine allgemeinste Vereinheitlichung. Diese kann mit Hilfe eines relativ einfachen Algorithmus ermittelt werden.
Resolution prädikatenlogischer Klauseln
Mit diesem Instrumentarium kann das Resolutionsverfahren auf Aussagen der Prädikatenlogik ausgeweitet werden.
- Seien
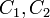 zwei Klauseln einer normalisierten prädikatenlogischen Aussage. darf vorausgesetzt werden, dass diese keine übereinstimmenden Variablen enthalten.
zwei Klauseln einer normalisierten prädikatenlogischen Aussage. darf vorausgesetzt werden, dass diese keine übereinstimmenden Variablen enthalten. - Seien
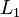 und
und 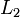 positive bzw. negiert vorkommende Literale in
positive bzw. negiert vorkommende Literale in 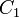 bzw.
bzw. 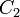 , die eine allgemeinste Vereinheitlichung
, die eine allgemeinste Vereinheitlichung 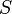 besitzen.
besitzen.
Dann heißt
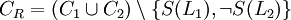 ein binärer Resolvent von
ein binärer Resolvent von 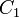 und
und 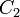 .
.
- Sei ferner
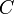 eine Klausel mit einer Teilmenge von Literalen, die eine allgemeinste Vereinheitlichung
eine Klausel mit einer Teilmenge von Literalen, die eine allgemeinste Vereinheitlichung 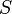 besitzt.
besitzt.
Dann heißt
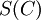 ein Faktor von
ein Faktor von 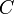 .
.
Ein Resolvent zweier Klauseln
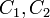 ist
ist- entweder ein binärer Resolvent von
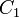 und
und 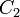 .
. - oder ein binärer Resolvent von
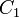 und eines Faktors von
und eines Faktors von 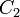 .
. - oder ein binärer Resolvent von eines Faktors von
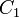 und
und 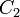 .
. - oder ein binärer Resolvent eines Faktors von
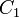 und eines Faktors von
und eines Faktors von 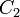 .
.
Das Resolutionsverfahren für prädikatenlogische Aussagen besteht darin, so lange solche Resolventen zu erzeugen, bis die leere Klausel erzeugt und damit der Widerspruchsbeweis erbracht ist.
Beispiel
Ein logisches Rätsel
Wir wollen das Prinzip am Beispiel eines kleinen, nicht wörtlich zu nehmenden logischen Rätsels illustrieren:
Seit dem Altertum ist bekannt, dass alle Athener klug (1) und alle Spartaner heldenmütig (2) sind. Außerdem ist bekannt, dass ein profundes Misstrauen zwischen beiden Städten herrscht, so dass doppelte Stadtbürgerschaften ausgeschlossen sind (3). Unser nach Griechenland entsandter Forscher war neulich zu Gast bei einer Konferenz. Mit Ausnahme unseres Forschers stammte jeder der Anwesenden aus einer der beiden Städte (4).
Der Forscher kam ins Gespräch mit den Herren Diogenes, Platon und Euklid. Mit ihren berühmten Vorbildern hatten diese nur den Namen gemein. Die Herren zogen kräftig übereinander vom Leder. Euklid sagte: „Wenn Platon Spartaner ist, dann ist Diogenes feige!“ (5) - Platon behauptete: „Diogenes ist auch dann eine Memme, wenn Euklid Spartaner ist!“ (6) „Wenn Diogenes allerdings Athener ist, dann ist Euklid ein Waschlappen!“ (7) - Worauf sich Diogenes den Bart glatt strich und postulierte: „Wenn Platon Athener ist, dann ist Euklid ein Dummkopf!“ (8)
Bei aller Spitzzüngigkeit blieben die drei Herren mit ihren Behauptungen bei der Wahrheit. Wer kommt aus welcher Stadt?
Das Rätsel in Klauselform
Wir setzen p für Platon, d für Diogenes, e für Euklid. Die Prädikate „ist Athener“, „ist Spartaner“, „ist heldenmütig“ und „ist klug“ bezeichnen wir mit A, S, H und K. Wir übersetzen die oben genannten Aussagen in die Klauselform und erhalten:
¬A(x) v K(x) (1) ¬S(x) v H(x) (2) ¬A(x) v ¬S(x) (3) A(x) v S(x) (4) ¬S(p) v ¬H(d) (5) ¬S(e) v ¬H(d) (6) ¬A(d) v ¬H(e) (7) ¬A(p) v ¬K(e) (8) Die Auflösung
Wir nehmen an, Platon sei Athener:
A(p) {Annahme} (9) Nun wenden wir das Resolutionsprinzip an und erhalten:
¬K(e) {aus Resolution von (9) mit (8)} (10) ¬A(e) {aus Substitution von e für x und Resolution (10,1)} (11) S(e) {Subs. (e:x), Res. (11,4)} (12) ¬H(d) {Res. (12,6)} (13) ¬S(d) {Subs. (d:x), Res. (13,2)} (14) A(d) {Subs. (d:x), Res. (14,4)} (15) ¬H(e) {Res. (15,7)} (16) ¬S(e) {Subs. (e:x), Res. (16,2)} (17) leere Klausel {Res. (17,12)} (18) Somit ist die Annahme (9) zum Widerspruch geführt. Sie ist mitsamt den aus ihr abgeleiteten Klauseln (10) bis (18) zu verwerfen. Wir erhalten stattdessen:
¬A(p) {da (9) falsch ist} (19) S(p) {Subs. (p:x), Res. (19,4)} (20) Nehmen wir nun an, Diogenes sei Spartaner, und wenden wir weiterhin das Resolutionsprinzip an:
S(d) {Annahme} (21) H(d) {Subs. (d:x), Res. (21,2)} (22) ¬S(p) {Res. (22,5)} (23) leere Klausel {Res. (23,20)} (24) Somit ist die Annahme (21) widerlegt und mitsamt den aus ihr abgeleiteten Klauseln (22) – (24) zu verwerfen. Wir erhalten stattdessen:
¬S(d) {da (21) falsch ist} (25) A(d) {Subs. (d:x), Res. (25,4)} (26) Nehmen wir an, Euklid sei Spartaner. Wir erhalten:
S(e) {Annahme} (27) H(e) {Subs. (e:x), Res. (27, 2)} (28) ¬A(d) {Res. (28, 7)} (29) leere Klausel {Res. (29,26)} (30) Also ist (27) falsch und samt (28) - (30) zu verwerfen. Wir erhalten stattdessen:
¬S(e) {da (27) falsch ist} (31) A(e) {Subs. (e:x), Res. (31,4)} (32) Platon ist Spartaner (20). Diogenes ist Athener (26), ebenso Euklid (32).
Terminierung und Komplexität
Im Falle der Aussagenlogik das Verfahren: Es liefert in endlicher Zeit ein Ergebnis, ob eine vorgelegte Aussage erfüllbar ist. Die Rechenzeit wächst im allgemeinen Fall und mit den derzeit bekannten Verfahren exponentiell mit der Anzahl der Literale, da es sich um ein Problem handelt.
Im Falle der Prädikatenlogik terminiert das Verfahren zwar stets mit dem korrekten Ergebnis, wenn ihm eine unerfüllbare Formel vorgelegt wird. Im allgemeinen Fall, bei einer erfüllbaren Formel, kommt es jedoch vor, dass das Verfahren kein Ende findet. Mit jedem Resolutionsschritt entstehen neue Klauseln, aber nicht die leere Klausel, die für den zu zeigenden Widerspruch steht. Man spricht also von . Wäre es anders, dann wäre das Resolutionsverfahren ein Algorithmus, um prädikatenlogische Formeln allgemein zu entscheiden - was unmöglich ist, da das Gültigkeitsproblem in der Prädikatenlogik nicht ist.
Andere Kalküle im logischen Einsatz
Quellen
- Davis, Martin: Eliminating the Irrelevant from Mechanical Proofs. in: Journal of Symbolic Logic, ISSN 0022-4812, Vol. 32, No. 1 (Mar., 1967), pp. 118-119
- Chang, Chin-Liang; Lee, Richard Char-Tung: Symbolic Logic and Mechanical Theorem Proving, Academic Press, 1973, ISBN 0-12-170350-9, S. 77ff
- Chang, Chin-Liang; Lee, Richard Char-Tung: Symbolic Logic and Mechanical Theorem Proving, Academic Press, 1973, ISBN 0-12-170350-9, S. 80-81
- Haken, A. "The Intractability of Resolution", Theoretical Computer Science 39 (1985), pp. 297-308.
Literatur
- Chang, Chin-Liang; Lee, Richard Char-Tung: Symbolic Logic and Mechanical Theorem Proving, Academic Press, 1973, ISBN 0-12-170350-9
Weblinks
- Vorlesungsskript von Habel und Eschenbach, 2002, Fachbereich Informatik, Universität Hamburg, mit anschaulichen grafischen Darstellungen
- Vorlesungsskript von Bernhard Beckert, 2006, Universität Koblenz-Landau
- Logic for Computer Scientists, von , Universität Koblenz-Landau
Wikimedia Foundation.

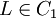
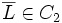
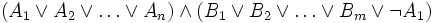
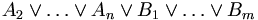
![[(A_1 \vee A_2 \vee \dots \vee A_n) \wedge (B_1 \vee B_2 \vee \dots \vee B_m \vee \neg A_1)] \rightarrow (A_2 \vee A_3 \vee \dots \vee A_n \vee B_1 \vee B_2 \vee \dots \vee B_m)](/pictures/dewiki/48/0d920861c8ddb727440683a423b46d1e.png)
![\equiv \neg [(A_1 \vee A_2 \vee \dots \vee A_n) \wedge (B_1 \vee B_2 \vee \dots \vee B_m \vee \neg A_1)] \vee (A_2 \vee A_3 \vee \dots \vee A_n \vee B_1 \vee B_2 \vee \dots \vee B_m)](/pictures/dewiki/54/6039b0a754365210a2122eceba651983.png)