Klauselnormalform

Die Klauselform oder Klauselnormalform beschreibt in der Logik eine Formel in konjunktiver Normalform (KNF), bei der die Konjunktionen jeweils in Mengenschreibweise zusammengefasst wurden.

Eine Formel in Klauselform (selten auch Klausenform) ist eine logische Verknüpfung von Literalen, notiert als disjunktive Normalform oder konjunktive Normalform, wobei festgelegt ist, dass die leere verallgemeinerte Disjunktion interpretiert den Wahrheitswert falsch ergibt und die leere verallgemeinerte Konjunktion interpretiert den Wahrheitswert wahr ergibt.

Klauselnormalformen sind über eine Transformation erstellbar und dienen zur maschinellen Beweisführung über logischen Formeln.

Beispiel 1

$((a \vee b) \wedge (b \vee c) \wedge (a \vee \neg d \vee \neg e) \wedge d)$

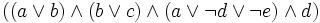
ist eine Formel in KNF, welche in Klauselform einfach so dargestellt wird:

$\{ \{a,b\}, \{b,c\}, \{a, \neg d, \neg e\}, \{d\} \}$

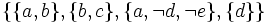
Diese Schreibweise ist kompakter und erleichtert beispielsweise den Test auf (Un)Erfüllbarkeit mittels Resolution.

Beispiel 2

Die aussagenlogische Formel 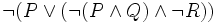$\neg(P\or (\neg(P\and Q)\and \neg R))$ soll in konjunktive Klauselform transformiert werden (verallgemeinerte Konjunktion):

$\{\neg(P\or (\neg(P\and Q) \and \neg R))\}$

$\{\{\neg P\}, \{\neg(\neg(P \and Q)\and \neg R))\}\}$

$\{\{\neg P\}, \{\neg \neg (P \and Q) , \neg \neg R\}\}$

$\{\{\neg P\}, \{(P \and Q), R\}\}$

$\{\{\neg P\}, \{P,R\}, \{Q, R\}\}$

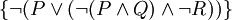
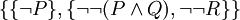
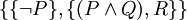
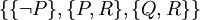
Hornklauseln

Hornklauseln stellen eine spezielle Klauselnormalform dar, bei der jede Klausel maximal ein positives Literal enthält.

• negative Hornklausel: Klausel enthält kein positives Literal
• positive Hornklausel: Klausel enthält ein positives Literal

Diese Schreibweise ist deswegen beliebt, da sich Hornklauseln schnell in eine Menge von Implikationen umformen lassen.

Beispiel

• Hornklausel: $\{ \{a, \neg b\}, \{ \neg c, \neg d\}, \{b\} \}$
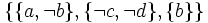
• Äquivalenter Ausdruck: $(\neg a \Rightarrow \neg b) \wedge (c \Rightarrow \neg d) \wedge (true \Rightarrow b)$
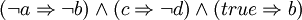
• Weitere mögliche Schreibweise: $(b \Rightarrow a) \wedge (c \wedge d \Rightarrow false) \wedge (true \Rightarrow b)$

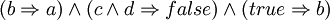
siehe auch: Horn-Formel