- Kleinsche Fläche
-
Die Kleinsche Flasche (auch Kleinscher Schlauch), benannt nach dem deutschen Mathematiker Felix Klein, ist ein geometrisches Objekt. Umgangssprachlich formuliert hat sie die Eigenschaft, dass innen und außen nicht unterschieden werden können, oder anders formuliert, dass sie nur eine einzige Seite besitzt, die gleichzeitig innen und außen ist. Dies wird in der Mathematik eine nicht-orientierbare Fläche genannt.
Wie auch das Möbiusband ist die Kleinsche Flasche eine zweidimensionale differenzierbare Mannigfaltigkeit, die nicht orientierbar ist. Im Gegensatz zum Möbiusband kann die Kleinsche Flasche nur mit Selbstdurchdringung in den dreidimensionalen Euklidischen Raum
 eingebettet werden. Ohne Selbstdurchdringung ist dies aber für den
eingebettet werden. Ohne Selbstdurchdringung ist dies aber für den 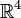 und höhere Dimensionen möglich.
und höhere Dimensionen möglich.Der Name „Kleinsche Flasche“ soll aus einem Übersetzungsfehler ins Englische entstanden sein. Ursprünglich soll dieses Objekt im Deutschen Kleinsche Fläche geheißen haben, und durch eine Verwechslung von Flasche und Flaeche als Klein Bottle übersetzt worden sein. Nachdem sich diese anschauliche Bezeichnung durchgesetzt hat, wird nun auch im Deutschen der Begriff Flasche verwendet.
Inhaltsverzeichnis
Formale Beschreibung
Die Kleinsche Flasche wird durch folgende Gleichungen dargestellt:
Für
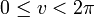 und
und 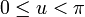 gilt:
gilt:- x = acos(u)(1 + sin(u)) + rcos(u)cos(v)
- y = bsin(u) + rsin(u)cos(v)
- z = rsin(v)
Für
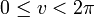 und
und 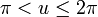 gilt:
gilt:- x = acos(u)(1 + sin(u)) + rcos(v + π)
- y = bsin(u)
- z = rsin(v)
Die Konstanten a und b verändern das Aussehen der Figur.
Konstruktion
Man beginnt mit einem Quadrat und klebt die Ecken und Ränder mit den entsprechenden Farben zusammen, so dass die Pfeile zueinander passen. Dies ist in der nachfolgenden Skizze dargestellt. Formell gesagt wird die kleinsche Flasche beschrieben durch die Quotiententopologie des Quadrates [0,1] × [0,1] mit Kanten, welche die folgende Relationen erfüllen: (0,y) ~ (1,y) für 0 ≤ y ≤ 1 und (x,0) ~ (1-x,1) für 0 ≤ x ≤ 1.
Das Quadrat ist ein Fundamentalpolygon der kleinschen Flasche.
Man beachte, dass diese Beschreibung das „Kleben“ in einem abstrakten Sinn meint, das versucht, die dreidimensionale kleinsche Flasche mit sich selbst überkreuzenden Kanten zu konstruieren. Faktisch hat die kleinsche Flasche keine sich überkreuzende Kanten. Dessen ungeachtet ist es eine Möglichkeit, dieses Objekt in seiner Konstruktion zu veranschaulichen.
Man klebe die roten Pfeile vom Quadrat zusammen (linke und rechte Kanten), so dass man einen Zylinder erhält. Man ziehe den Zylinder etwas auseinander und klebe weiterhin die Enden so zusammen, dass die Pfeile auf den Kreis passen. Dabei wird die Kreisfläche der einen Zylinderfläche durch die der anderen geschoben. Beachte, dass dieser Vorgang zur Überkreuzung von Kanten führt. Man bezeichnet dies als Immersion der kleinschen Flasche im dreidimensionalen Raum.
Bettet man die kleinsche Flasche in den vierdimensionalen reellen Raum ein, kann eine Selbstdurchdringung vermieden werden. Anschaulich geschieht dies folgendermaßen: Man nimmt die oben abgebildete Immersion in den dreidimensionalen Raum und belässt die vierte Koordinate zunächst bei null. In der Nähe der Selbstdurchdringung erhöht man den Wert der vierten Koordinate für eine der (lokalen) Komponenten stetig auf eins und senkt sie danach wieder ab. Grafisch lässt sich die vierte Koordinate durch eine unterschiedliche Farbwahl veranschaulichen.
Siehe auch
Weblinks
- Die Kleinsche Flasche, aus Glas gefertigt von Clifford Stoll
- Die Banchoff-Kleinsche Flasche
- Darstellende Geometrie im weiteren Sinn
- „Kleinsche Flaschen aus Glas“ von Ian Stewart
- „Mathematiker häkeln vierdimensionale Wollmützen“ von Imker Peter
- Konstruktion von 2D-Mannigfaltigkeiten
- Bouteille de Klein (französisch, gute Abbildungen)
- Konstruktion der Kleinschen Flasche als Video.
Wikimedia Foundation.








