Kobon-Dreiecke

Kobon-Dreiecke sind Dreiecke, die durch Zeichnen mehrerer Gerade entstehen. Das dazugehörige Kobon-Dreiecke-Problem ist, wie viele nicht-überlappende Dreiecke N(k) sich maximal erzeugen lassen, wenn man k Geraden in die Ebene zeichnet^[1]. Der Namensgeber Kobon Fujimura, ein japanischer Mathematiklehrer und Puzzleautor, veröffentlichte die Aufgabenstellung in seinem 1978 erschienen Buch "The Tokyo Puzzle".

Kobon-Zahl

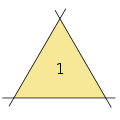
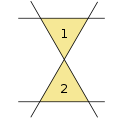
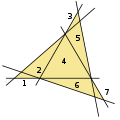
Für bis zu sechs Geraden ist es einfach, durch Ausprobieren Anordnungen zu finden, die möglichst viele Dreiecke formen. Während mit drei Geraden nur ein Dreieck gebildet werden kann, sind es für vier, fünf und sechs Geraden maximal 2,5 respektive 7.

• 

  Aus drei Geraden lässt sich ein Dreieck erzeugen.

• 

  Zwei Dreiecke aus vier Geraden

• 

  Fünf Dreiecke aus fünf Geraden

• 

  Sieben Dreiecke aus sechs Geraden

• 

  Elf Dreiecke aus sieben Geraden

Wie viele Dreiecke sich für eine beliebige Anzahl Geraden k erzeugen lassen (die sogenannte Kobon-Zahl), ist ein bisher ungelöstes Problem der kombinatorischen Geometrie, dessen Lösung als sehr schwer vermutet wird^[2].

Obere Schranke

Der folgende Beweis von Saburo Tamura ermöglicht es, für ein gegebenes k das Maximum der Kobon-Zahl zu bestimmen. Jede der k Geraden schneidet die restlichen k-1-Linien höchstens einmal. Die k-1-Schnittpunkte formen k-2 Liniensegmente (Zaunpfahlproblem), wodurch also die Figur total maximal k*(k-2) Segmente aufweist (im oben gezeigten Beispiel für k=5 sind beispielsweise 15 Segmente entstanden). Jedes freistehende Dreieck benötigt nun genau drei dieser Liniensegmente, außer es teilt eine oder mehrere Kanten mit einem weiteren Dreieck (z.B. im Beispiel k=6). In diesen Fällen müssen jedoch pro zwei Dreiecke sich drei Geraden in einen Punkt schneiden, was die Anzahl der Liniensegmente um drei verringert - mehr als die zwei eingesparten Liniensegmente.

Somit benötigt jedes Dreieck (mindestens) drei Segmente, wodurch

$\lfloor k\left(k-2\right)/3\rfloor$

eine obere Schranke für die maximale Anzahl an nicht-überlappenden Dreiecken aus k Geraden bildet. Die daraus resultierende Sequenz ist die Folge A032765 in OEIS. Die Schranke wird nicht immer erreicht, so lassen sich mit 6 Geraden maximal 7 Dreiecke - somit ein Dreieck weniger als die obere Schranke - bilden. Dies lässt sich mit weiterführenden Überlegungen erklären, aus welchen die engere obere Schranke

$\lfloor k\left(k-2\right)/3\rfloor - \chi_{\{ n | (n\mod 6) \in \{0,2\} \}}(n)$

von Clément und Bader hervorgeht ^[3]. χ bezeichnet dabei die charakteristische Funktion.

Bekannte Lösungen

Größte bekannte perfekte Lösung (85 Dreiecke aus 17 Geraden)

Perfekte Lösungen, also Kobon-Dreiecke, welche die obere Schranke erreichen, sind bekannt für k = 3, 4, 5, 6, 7, 8, 9, 13, 15 und 17.^[2] Außer für diese k ist die maximale Anzahl an Dreiecken nicht bekannt. Für k = 10 und 11 enthält die beste bekannte Lösung ein Dreieck weniger als die obere Schranke, für k = 12, 16 und 18 zwei Dreiecke weniger.

Die folgende Auflistung zeigt die obere Schranke sowie die beste bekannte Lösung für verschiedene k.

k	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	...
Obere Schranke für N(k)	1	2	5	7	11	15	21	26	33	40	47	55	65	74	85	95	107	119	133	...
Beste bekannte Lösung	1	2	5	7	11	15	21	25	32	38	47	53	65	72	85[3]	93	104	115	130	...

Die bekannten Kobon-Dreieckszahlen sind fett gedruckt. Sie sind die Folge A006066 in OEIS.

Weblinks

1. ↑ Kobon Triangle bei Mathworld
2. ↑ ^{a b} Kolumne von Ed Pegg Jr. auf Math Games
3. ↑ ^{a b} Verschiedene Lösungen und Beweis für obere Schranke