Kommutatoruntergruppe

In der Mathematik bezeichnet die Kommutatorgruppe (oder Kommutator-Untergruppe) zu einer Gruppe G diejenige Untergruppe, die von den Kommutatoren von G erzeugt wird:

$K(G) = \langle\{[a,b]\ |\ a,b\in G\}\rangle,\qquad [a,b]=aba^{-1}b^{-1}.$

Die Kommutatorgruppe wird auch mit [G,G] bezeichnet.

Im Allgemeinen ist die Menge aller Kommutatoren keine Untergruppe von G, die Phrase erzeugt von in der Definition kann also nicht weggelassen werden.

Eigenschaften

K(G) ist Normalteiler von G, da für alle 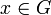$x\in G$ gilt: x ^{− 1}[a,b]x = [x ^{− 1}ax,x ^{− 1}bx].

Die Kommutatorgruppe misst, wie weit eine Gruppe von Kommutativität entfernt ist. G ist genau dann abelsch, wenn K(G) = {e}. Ist G = K(G), nennt man G eine perfekte Gruppe.

Die Faktorgruppe G / K(G) ist stets abelsch, sie wird als Abelisierung der Gruppe bezeichnet. Für jeden Normalteiler N gilt:

G / N ist genau dann abelsch, wenn $K(G) \subseteq N.$

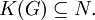
Das heißt, die Kommutatorgruppe ist der kleinste Normalteiler, für den die Faktorgruppe abelsch ist.

Beispiel

Es sei S_n die symmetrische Gruppe und A_n die alternierende Gruppe. Dann gilt:

• K(S_n) = A_n für $n\geq 2.$
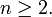
• K(A_n) = A_n für $n\geq 5.$
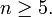
• K(A₄) = V, wobei V die Kleinsche Vierergruppe bezeichnet.
• K(A₃) = K(A₂) = {e}.

Höhere Kommutatorgruppen

Das Bilden der Kommutatorgruppe lässt sich iterieren, man bezeichnet die n-te Kommutatorgruppe mit K_n(G). Die rekursive Definition lautet:

1. K₀(G): = G.
2. K_{n + 1}(G): = K(K_n(G)).

Eine Gruppe G heißt auflösbar genau dann, wenn eine Kette von sukzessiven Normalteilern 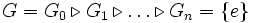$G=G_0\triangleright G_1\triangleright\ldots\triangleright G_n=\{e\}$ (Subnormalreihe) existiert, so dass die Faktorgruppen G_k / G_{k + 1} abelsch sind. Die Konstruktion der iterierten Kommutatorgruppe liefert ein Kriterium für die Auflösbarkeit von G:

G ist genau dann auflösbar, wenn es ein $n \in \mathbb{N}$ gibt mit K_n(G) = {e}.

In der Tat ist die bei fortgesetzter Kommutatorbildung entstehende absteigende Reihe von Untergruppen oder eine Verfeinerung dieser Reihe äquivalent zu jeder solchen Subnormalreihe oder einer Verfeinerung derselben.

Der Zusammenhang zwischen den beiden äquivalenten Definitionen der Auflösbarkeit, über fortgesetzte Kommutatorenbildung einerseits und über eine Subnormalreihe andererseits sowie der Begriff der Subnormalreihe werden im Artikel „Reihe (Gruppentheorie)“ erläutert.

Beispiel

Die symmetrische Gruppe S_n bzw. die alternierende Gruppe A_n ist genau dann auflösbar, wenn n < 5. Für 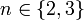$n\in\{2,3\}$ sieht man das sofort mit obigem Beispiel ein. Für n = 4 gilt:

K(S₄) = A₄, K(A₄) = V, K(V) = {e}, da V abelsch ist.

Für 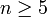$n\geq 5$ wird die Kette der iterierten Kommutatorgruppen stationär bei 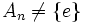$A_n \neq \{e\}$, also ist dann weder S_n noch A_n auflösbar.