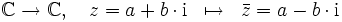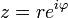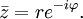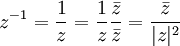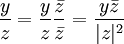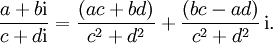- Komplex konjugiert
-
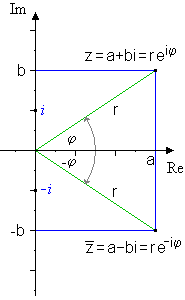
Komplexe Zahl z = a + bi und
ihre Konjugierte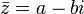
In der Mathematik bezeichnet man als komplexe Konjugation die Abbildung
im Körper der komplexen Zahlen. Sie ist ein Körperautomorphismus von
 , also mit der Addition und Multiplikation verträglich:
, also mit der Addition und Multiplikation verträglich: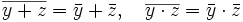 .
.
Die zu
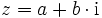 konjugierte Zahl
konjugierte Zahl 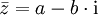 hat also denselben Realteil, aber den entgegengesetzten Imaginärteil.
hat also denselben Realteil, aber den entgegengesetzten Imaginärteil.In der Exponentialform ist die Konjugierte der Zahl
die Zahl
Sie hat also bei unverändertem Betrag gerade den negativen Winkel von z. Man kann die Konjugation in der komplexen Zahlenebene also als die Spiegelung an der reellen Achse identifizieren. Insbesondere werden bei der Konjugation genau die reellen Zahlen wieder auf sich selbst abgebildet.
Inhaltsverzeichnis
Rechenregeln
Für alle komplexen Zahlen
 gilt:
gilt:Anwendung
Mit Hilfe der Konjugation können die Inverse und auch der Quotient komplexer Zahlen bequem angegeben werden:
- Zu
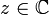 mit
mit 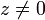 ist
ist
-
- das multiplikativ Inverse.
- Für die Division zweier komplexer Zahlen erhalten wir:
-
- oder ausführlicher:
Komplexe Konjugation bei Matrizen
Die komplex Konjugierte einer Matrix ist die Matrix, deren Komponenten die komplex konjugierten Komponenten der ursprünglichen Matrix sind. Die Transposition einer zuvor komplex konjugierten Matrix wird hermitesche Transposition genannt. Für Matrizen auf dem Euklidischen Raum gilt weiterhin, dass die hermitesch transponierte Matrix identisch ist mit der adjungierten Matrix.
Verallgemeinerung
In der abstrakten Algebra wird dieser Begriff folgendermaßen erweitert:
Zwei über K algebraische Elemente einer Körpererweiterung L / K heißen zueinander konjugiert, wenn sie dasselbe Minimalpolynom über K haben. Die Nullstellen des Minimalpolynoms von a in L heißen „Konjugierte von a (in L)“. Jeder K-Automorphismus von L (d. h. ein L-Automorphismus, der K punktweise festhält) bildet a auf eine seiner Konjugierten ab.
Wikimedia Foundation.