Komponente (Graphentheorie)

Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!

Sei das Paar (V,E) = :G ein ungerichteter Graph (Graphentheorie) mit der Knotenmenge V und der Kantenmengen E.

Kantenfolge

Die endliche alternierende Folge v₀,e₁,v₁,...,v_{n − 1},e_n,v_n mit den Knoten v_i aus V und den Kanten e_i aus E heißt genau dann Kantenfolge der Länge n vom Knoten v₀ zum v_n, wenn für alle 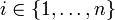$i\in\{1, \ldots, n\}$ gilt, dass e_i = {v_{i − 1},v_i}.

verbindbar

Zwei Knoten v, v' aus V heißen genau dann verbindbar in G, wenn eine Kantenfolge vom Knoten v zu dem Knoten v' in G existiert

zusammenhängend

G heißt genau dann zusammenhängend, wenn für alle paarweise verschiedenen Knoten aus V gilt, dass sie verbindbar sind.

Nun könnte man intuitiv formulieren, dass eine Komponente von G ein maximal zusammenhängender Untergraph von G ist. Dann wäre ein Graph genau dann zusammenhängend, wenn er aus genau einer Komponente besteht.

Etwas formaler kann man sich über legen, dass die Beziehung "verbindbar", die zwischen zwei Knoten bestehen kann, eine Äquivalenzrelation ist. Trivialerweise ist jeder Knoten mit sich selbst verbindbar (Reflexive Relation). Außerdem, ist ein Konten v mit einem Knoten v' verbindbar, dann gilt dies auch umgekehrt (Symmetrische Relation). Ist schließlich ein Knoten v mit einem Knoten v' verbindbar, welcher wiederum mit einem Knoten v'' verbindbar ist, dann ist offenbar auch v mit v'' verbindbar (Transitive Relation).

Erzeugter Untergraph

Sei V_U eine Teilmenge von V. Sei weiter E_U die Teilmenge von E, die entsteht, wenn man aus E alle Kanten entfernt die einen Knoten enthalten, der nicht in V_U ist. Genau dann heißt das Paar (V_U,E_U) der von V_U erzeugte Untergraph von G.

Komponente

Ein Untergraph U von G heißt genau dann Komponente von G, wenn die Knotenmenge V_U von U eine Äquivalenzklasse auf V bezüglich der Beziehung verbindbar ist, und U der durch V_U erzeugte Untergraph von G ist.

Literatur

• Lutz Volkmann: Fundamente der Graphentheorie, Springer, Wien (Dezember 2001), ISBN 3-211-82774-9
• Reinhard Diestel: Graphentheorie. Springer 2006, ISBN 3-540-21391-0 (elektronische Online-Version)

Weblinks

• Graph Theory with Applications Die elektronische Ausgabe des Buches "Graph Theory with Applications" von J.A. Bondy und U.S.R. Murty
• Vorlesungen zur Graphentheorie Die elektronische Ausgabe des Buches "Fundamente der Graphentheorie" von L. Volkmann
• Graphentheorie Die elektronische Ausgabe des Buches "Graphentheorie" von R. Diestel