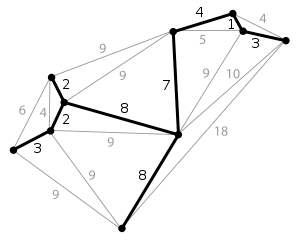
Aufspannender Baum

Ein Graph mit einem minimalen Spannbaum.

Ein Spannbaum (auch aufspannender Baum oder manchmal spannender Baum genannt; englisch spanning tree) ist in der Graphentheorie ein Teilgraph eines ungerichteten Graphen, der ein Baum ist und alle Knoten dieses Graphen enthält. Spannbäume existieren nur in zusammenhängenden Graphen.

Ein Teilgraph, der in einem Graphen für jede Komponente einen Spannbaum ergibt, wird Gerüst, Spannwald oder aufspannender Wald genannt. Dabei muss der Graph nicht notwendigerweise zusammenhängend sein. In zusammenhängenden Graphen sind Gerüst und Spannbaum identische Begriffe, während Spannbäume für unzusammenhängende Graphen nicht definiert sind.

In kantengewichteten Graphen lässt sich als Gewicht eines Graphen die Summe seiner Kantengewichte definieren. Ein Spannbaum bzw. ein Gerüst heißt minimal, wenn kein anderer Spannbaum bzw. kein anderes Gerüst in demselben Graphen mit geringerem Gewicht existiert. Häufig wird minimaler Spannbaum auch mit MST (Abkürzung des englischen Begriffs Minimum Spanning Tree) oder MCST (Minimum Cost Spanning Tree - ein Spannbaum mit minimalen Kosten) abgekürzt. Statt minimales Gerüst sagt man auch Minimalgerüst.

Wichtige Algorithmen

Zum Finden eines minimalen Spannbaumes gibt es u.a. den Algorithmus von Kruskal und den Algorithmus von Prim. Letzterer ist der effizientere und besitzt die Worst-Case-Laufzeit 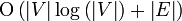$\mathrm{O} \left( \left| V \right| \log \left( \left| V \right| \right) + \left| E \right| \right)$. Allerdings benötigt er dafür eine recht komplexe Datenstruktur, die sogenannten Fibonacci-Heaps. Es kann gezeigt werden, dass der Algorithmus von Prim optimal ist, da mit seiner Hilfe auch Zahlen sortiert werden können.

Anwendungen

Die Berechnung minimaler Spannbäume findet direkte Anwendung in der Praxis, beispielsweise für die Erstellung von kostengünstigen zusammenhängenden Netzwerken, wie beispielsweise Telefonnetze oder elektrische Netze. Auch bei Computernetzwerken mit redundanten Pfaden werden zur Vermeidung von Paketverdopplungen Spannbäume genutzt (siehe Spanning Tree Protocol).

In der Graphentheorie selbst sind MST-Algorithmen häufig Grundlage komplexerer Algorithmen für schwierigere Probleme. Die Berechnung minimaler Spannbäume ist zum Beispiel Bestandteil von Approximationsalgorithmen für das Problem des Handlungsreisenden, oft auch Traveling-Salesman-Problem genannt (siehe MST-Heuristik), oder für das Steinerbaum-Problem. Letzteres ist auch eine Verallgemeinerung des Problems, einen minimalen Spannbaum zu finden.

Des Weiteren spielen Spannbäume bei der algorithmischen Erzeugung von Labyrinthen eine Rolle. Ein Knoten im Spannbaum entspricht dabei einem Feld, während eine Kante einen möglichen Übergang zu einem Nachbarfeld darstellt. Eine fehlende Kante beschreibt folglich eine Wand. Da Spannbäume wie alle Bäume zyklenfrei sind, besitzt ein mittels Spannbäumen erzeugtes Labyrinth stets nur einen einzigen Lösungsweg.

Literatur

• Effiziente Algorithmen und Datenstrukturen II. Vorlesungsmitschrift, Technische Universität München, 2004, Seite 28.
• Jaroslav Nesetril, Eva Milková, Helena Nesetrilová: Otakar Borůvka on minimum spanning tree problem: Translation of both the 1926 papers, comments, history, Discrete Mathematics, 233 (2001), Seiten 3–36.
• Bernard Chazelle: A minimum spanning tree algorithm with inverse-Ackermann type complexity. Journal ACM 47 (2000), Seiten 1028–1047.

Weblinks

• Minimal spannende Bäume, Ronny Harbich, 2006
• Katharina Langkau, Martin Skutella: Minimal aufspannende Bäume, Algorithmus der Woche, 25. Juli 2006. Fakultätentag Informatik.