Kontingenzanalyse

Der Kontingenzkoeffizient C (nach Karl Pearson) ist ein statistisches Zusammenhangsmaß. Der Pearsonsche Kontingenzkoeffizient drückt die Stärke des Zusammenhangs zwischen zwei (oder mehreren) nominalen oder ordinalen Variablen aus. Er basiert auf dem Vergleich von tatsächlich ermittelten Häufigkeiten zweier Merkmale mit den Häufigkeiten, die man bei Unabhängigkeit dieser Merkmale erwartet hätte.

χ²-Koeffizient (Chi-Quadrat)

Der χ²-Koeffizient ist abhängig von der Größe der Kontingenztafel und n und gibt ein Maß für die "Stärke" des Zusammenhanges der beiden betrachteten Merkmale an:

$\sum_{i=1}^k \sum_{j=1}^m \frac{(h_{i,j} -\frac{h_i. h._j}{n})^2}{\frac{h_i. h._j}{n}}$

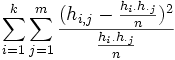
Zum Beispiel sei folgende Kontingenztafel gegeben:

	Limousine	Kombi	Summen
Arbeiter	19	18	37
Angestellte	43	20	63
Summen	62	38	100

Berechnung des χ²-Koeffizienten:

$\frac{(19 -\frac{37 * 62}{100})^2}{\frac{37 * 62}{100}} + \frac{(18 -\frac{37 * 38}{100})^2}{\frac{37 * 38}{100}} + \frac{(43 -\frac{63 * 62}{100})^2}{\frac{63 * 62}{100}} + \frac{(20 -\frac{63 * 38}{100})^2}{\frac{63 * 38}{100}} = 2,83$

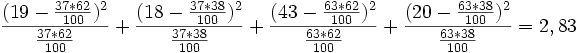
Der Aussagewert des χ²-Koeffizienten ist aber gering; jedoch wird er benötigt, um den Kontingenzkoeffizienten C zu ermitteln.

Zum Test vergleiche den Chi-Quadrat-Vierfeldertest.

Kontingenzkoeffizient C (auch CC oder K) nach Karl Pearson

χ² kann grundsätzlich sehr große Werte annehmen und ist nicht auf das Intervall [0,1] beschränkt. Dazu wird aus dem χ² der sogenannte Kontingenzkoeffizient nach Karl Pearson ermittelt:

$C=\sqrt{\frac{\chi ^2}{\chi^2 + n}}$.

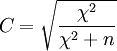Dabei ist n die Fallzahl und χ² ein Maß für den Unterschied zwischen beobachteten und erwarteten Häufigkeiten.

Dieser kann Werte zwischen 0 und 1 annehmen. Problematisch ist, dass dieser Kontingenzkoeffizient abhängig von der Anzahl der betrachteten Dimensionen ist, und so nur selten den Wert 1 annehmen kann. Unabhängig von der Anzahl der betrachteten Dimensionen ist der Koeffizient Cramer's V.

Korrigierter Kontingenzkoeffizient K*

Wenn k = min( | I | , | J | ) das Minimum aus der Anzahl der möglichen Merkmalausprägungen ist, dann gilt $C\in \left[0,\sqrt{\frac{k-1}{k}} \right]$. Daher benutzt man auch häufig den korrigierten Kontigenzkoeffizient: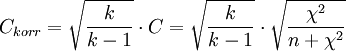

$C_{korr}=\sqrt{\frac{k}{k-1}} \cdot C = \sqrt{\frac{k}{k-1}} \cdot \sqrt{\frac{\chi ^2}{n+\chi ^2}}$.

Ein C_korr nahe 0 deutet dabei auf unabhängige Merkmale hin, ein C_korr in der Nähe von 1 dagegen auf ein hohes Maß an Abhängigkeit.

Der Kontingenzkoeffizient C relativiert den χ²-Koeffizienten um die Größe von n.

Der Kontingenzkoeffizient C führt schließlich zum korrigierten Kontingenzkoeffizienten.

Der korrigierte Kontingenzkoeffizient K* berechnet sich wie folgt:

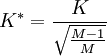$K^* = \frac{K}{\sqrt{\frac{M - 1}{M}}}$ wobei M = M_min(k,m)

im Beispiel: $K^* = \frac{0,166}{\sqrt{\frac{2 - 1}{2}}} = 0,235$

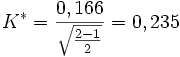
K* ist ein Zusammenhangmaß zwischen den Merkmalen. Je näher er an 0 liegt, desto geringer ist der Zusammenhang; je weiter er sich 1 nähert desto größer ist der Zusammenhang.

Mittlere quadratische Kontingenz

Ein weiteres Maß, um die Stärke der Abhängigkeit der Merkmale in einer Kontingenztafel anzugeben, ist die mittlere quadratische Kontingenz, die im Wesentlichen eine Erweiterung des χ²-Koeffizienten darstellt:

$\frac{1}{N} \sum_{i=1}^k \sum_{j=1}^m \frac{(h_{i,j} -\frac{h_i. h._j}{n})^2}{\frac{h_i. h._j}{n}}$

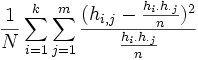
Je größer dieses Maß ist, desto stärker ist der Zusammenhang zwischen den zwei analysierten Merkmalen. Sind die beiden Merkmale unabhängig, so wird jeder Summand durch den Nenner des Bruches zu 0, das Maß selbst damit auch. Im Falle einer 2x2 Kontingenztafel ist das Maß normiert, nimmt also Werte im Intervall [0,1] an.

Siehe auch

Vierfeldertest