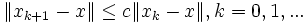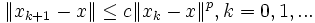Konvergenzordnung

Unter Konvergenzgeschwindigkeit (auch Konvergenzordnung) versteht man die Geschwindigkeit, mit der sich die Glieder einer konvergenten Folge (x_i) dem Grenzwert x nähern.

Man unterscheidet zwischen linearer, superlinearer sowie p-ter Konvergenzordnung.

Lineare Konvergenzgeschwindigkeit liegt vor, falls es ein 0<c<1 gibt, so dass

$\|x_{k+1}-x\| \leq c\|x_{k}-x\|, k=0,1,...$

Es handelt sich um superlineare Konvergenz, falls die Folge schneller als linear konvergiert. Dies liegt beispielsweise vor, wenn die obige Ungleichung nicht nur mit einem konstanten c gilt, sondern sogar mit einer gegen Null konvergenten Zahlenfolge (c_k).

Konvergenz der Ordnung p mit p>1 bedeutet, dass ein c>0 existiert, so dass

$\|x_{k+1}-x\| \leq c\|x_{k}-x\|^{p}, k=0,1,...$

Für p=2 spricht man von quadratischer Konvergenz.

Der Begriff ist vor allem in der Numerik wichtig, wo eine Näherung des Grenzwertes eines Iterationsverfahrens meist durch Berechnung einer kleinen Anzahl von Folgengliedern geschieht. Konvergenz der Ordnung p bedeutet dann, dass in jedem Iterationsschritt die Anzahl der genauen Dezimalstellen ver-p-facht werden, also beispielsweise bei quadratischer Konvergenz verdoppelt.

Die schnellere Konvergenz von Verfahren höherer Ordnung wird meist mit größerem Aufwand pro Iteration bezahlt, in vielen Fällen auch mit schlechteren Stabilitätseigenschaften.

Beispiele

Das Newton-Verfahren konvergiert bei einer einfachen Nullstelle mit zweiter Ordnung. Vereinfachte Varianten des Newton-Verfahrens konvergieren langsamer, teilweise superlinear, teilweise mit erster Ordnung.

Fixpunktverfahren, beispielsweise Splitting-Verfahren, haben eine Konvergenzgeschwindigkeit von 1. Im Vergleich zum Newton-Verfahren ist eine Fixpunkt-Iteration allerdings deutlich günstiger.