LOGSPACE-Reduktion

Eine logarithmisch platzbeschränkte Reduktion (auch als logarithmische Reduktion bezeichnet) ist eine spezielle Form der Reduktion.

Neben der Forderung, dass eine Sprache L' auf eine andere Sprache L mittels einer Funktion 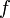$f\;$ reduzierbar ist, muss diese Funktion für eine logarithmische Reduktion zusätzlich auf logarithmischem Platz berechnet werden können.

Logarithmische Reduktionen werden in der Komplexitätstheorie üblicherweise verwendet, um nachzuweisen, dass eine Sprache der Komplexitätsklasse NL auch NL-vollständig ist.

Als Schreibweise wird hierbei häufig 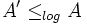$A' \le_{log} A$ verwendet.

Man beachte, dass für diese Reduktion die Transitivität gezeigt werden kann. Nur dadurch kann man mit diesem Begriff arbeiten.