NL-Vollständigkeit

In der Komplexitätstheorie bezeichnet NL die Klasse der Entscheidungsprobleme, die von einer nichtdeterministischen Turingmaschine auf logarithmischem Platz gelöst werden können.

NL ist eine Erweiterung der Klasse L, die analog für deterministische Turingmaschinen definiert ist.

Eigenschaften

Nach dem Satz von Immerman/Szelepcsenyi ist die Klasse NL unter Komplement abgeschlossen, es gilt also NL=CoNL.

Beziehung zu anderen Komplexitätsklassen

Da NL die Generalisierung der Klasse L ist, ist jedes Problem in L auch in NL. Darüber hinaus sind die folgenden Beziehungen bekannt:

L ⊆ NL ⊆ NC ⊆ P ⊆ NP ⊆ PSPACE

In obiger Kette ist für keine Inklusion bekannt, ob sie echt ist. Die einzigen transitiven Inklusionen, für die die Echtheit bekannt ist, sind:

• L ⊂ PSPACE
• NL ⊂ PSPACE

Dies ergibt sich aus dem Platzhierarchiesatz. Für die zweite Zeile wird noch der Satz von Savitch benötigt.

Bekannt ist allerdings, dass die Gleichheit NL=RL gilt. Die Klasse RL ist analog zu NL für probabilistische Turingmaschinen definiert.

NL-vollständige Probleme

Die Klasse NL enthält vollständige Probleme. Dies bedeutet, dass ein Problem nicht nur selbst in NL liegt, sondern dass sich weiterhin jedes andere Problem der Klasse NL auf dieses Problem reduzieren lässt. Die Berechnung der Reduktionsfunktion benötigt dabei ebenfalls nur logarithmisch viel Platz.

Erreichbarkeitsproblem in Graphen

Das Entscheidungsproblem, ob in einem gerichteten Graphen ein Weg zwischen zwei gegebenen Knoten existiert (STCON), ist NL-vollständig.

2-SAT

Ein weiteres wichtiges NL-vollständiges Problem ist 2-SAT, eine eingeschränkte Variante des NP-vollständigen Erfüllbarkeitsproblems der Aussagenlogik. Bei 2-SAT soll entschieden werden, ob eine gegebene aussagenlogische Formel erfüllt werden kann, die in konjunktiver Normalform mit jeweils zwei Literalen pro Klausel vorliegt. Eine mögliche Probleminstanz wäre

$(x_1 \vee \neg x_3) \wedge (\neg x_2 \vee x_3) \wedge (\neg x_1 \vee \neg x_2)$.

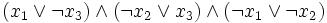Die richtige Antwort für diese Formel lautet "ja", da beispielsweise x₁ = 1,x₂ = 0,x₃ = 1 eine erfüllende Belegung der Variablen darstellt.

Weblinks

• NL im Complexity Zoo (englisch)