- Lambdaviertelplättchen
-
Eine Wellen- oder Verzögerungsplatte (auch: λ/n-Plättchen) ist ein optisches Gerät, das die Polarisation und Phase von durchtretendem Licht ändern kann. Folgende Arten gibt es:
- Ein λ/4-Plättchen verzögert Licht, das parallel zu einer Bauteil-spezifischen Achse polarisiert ist, um eine viertel Wellenlänge – bzw. π/2 – gegenüber dazu senkrecht polarisiertem Licht. Es kann bei richtiger Einstrahlung aus linear polarisiertem Licht zirkular oder elliptisch polarisiertes Licht machen und aus zirkular polarisiertem Licht wieder linear polarisiertes.
- Ein λ/2-Plättchen verzögert Licht, das parallel zu einer Bauteil-spezifischen Achse polarisiert ist, um eine halbe Wellenlänge – bzw. π – gegenüber dazu senkrecht polarisiertem Licht. Es kann die Polarisationsrichtung von linear polarisiertem Licht um einen wählbaren Winkel drehen.
Die Polarisationsänderungen kommen dadurch zustande, dass das Licht in zwei senkrecht stehende Polarisationsrichtungen zerlegt werden kann, die die Wellenplatte mit unterschiedlicher Geschwindigkeit passieren, deren Phasen also gegeneinander verschoben werden. Ein solches Plättchen besteht typischerweise aus einem doppelbrechenden Kristall (z. B. Kalzit) mit passend gewählter Dicke und Ausrichtung. Heutzutage erreicht man den gleichen Effekt aber auch schon in Folien, sodass es auch Verzögerungsfolien gibt. Trotzdem scheint es aber bei dem Sprachgebrauch des „Plättchens“ zu bleiben.
Inhaltsverzeichnis
Funktionsweise
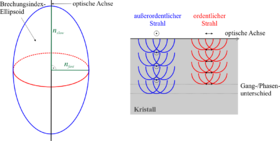 Diese Abbildung zeigt den sog. Brechzahlellipsoid für ein optisch positiv einachsiges Material, mit den zwei unterschiedliche Brechzahlen. Daneben ist gezeigt, wie sich zwischen ordentlichem und außerordentlichem Strahl (unterscheiden sich durch ihre Polarisation) ein Gang- (also auch Phasen-)Unterschied aufbaut, wenn die optische Achse senkrecht zur Einfallsrichtung steht. Über der Kristallgrenzfläche sind die unterschiedlichen Polarisationen des Lichtes angegeben. Die Kreise geben jeweils die Position einer Wellenfront an, die sich mit c/n durch den Kristall bewegt und von einem einzelnen Erregungszentrum ausgeht
Diese Abbildung zeigt den sog. Brechzahlellipsoid für ein optisch positiv einachsiges Material, mit den zwei unterschiedliche Brechzahlen. Daneben ist gezeigt, wie sich zwischen ordentlichem und außerordentlichem Strahl (unterscheiden sich durch ihre Polarisation) ein Gang- (also auch Phasen-)Unterschied aufbaut, wenn die optische Achse senkrecht zur Einfallsrichtung steht. Über der Kristallgrenzfläche sind die unterschiedlichen Polarisationen des Lichtes angegeben. Die Kreise geben jeweils die Position einer Wellenfront an, die sich mit c/n durch den Kristall bewegt und von einem einzelnen Erregungszentrum ausgehtBei einer Wellenplatte handelt es sich um eine dünne Scheibe von optisch anisotropem Material, also Material, welches für unterschiedlich polarisiertes Licht verschiedene Ausbreitungsgeschwindigkeiten c/n (bzw. verschiedene Brechzahlen n) in verschiedenen Richtungen aufweist. Oft verwendete Materialien sind optisch einachsig, das heißt es gibt zwei zueinander senkrechte Achsen im Kristall, entlang derer sich die Brechzahlen unterscheiden. Man nennt diese ordentliche (das Licht ist senkrecht zur optischen Achse polarisiert) und außerordentliche Achse (das Licht ist parallel zur optischen Achse polarisiert). Die Schwingungsrichtung des Lichtes, bei der eine Welle die größere Ausbreitungsgeschwindigkeit hat, heißt „schnelle Achse“, die dazu senkrecht stehende Richtung entsprechend „langsame Achse“. Im Folgenden soll die Funktionsweise eines solchen Wellenplättchens aus einem optisch positiv einachsigen Material (z. B. Quarz) beschrieben werden. Dabei fällt die langsame Achse mit der optischen Achse des Kristalls (Achse hoher Symmetrie im Kristallgitter) zusammen. Die Brechzahlen entlang dieser Achsen seien mit nfast und nslow bezeichnet. Für Wellenplättchen schneidet man die Kristalle so, dass ihre optische Achse in der polierten Eintrittsfläche liegt. An käuflich erhältlichen Plättchen wird üblicherweise die schnelle Achse markiert, sodass die Ausrichtung genau festgelegt werden kann.
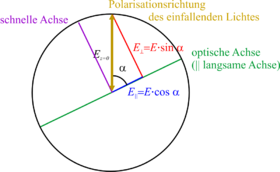 Dies Abbildung zeigt, wie ein unter dem Winkel α zur optischen Achse polarisierter Strahl auf das Plättchen fällt und das elektrische Feld auf die schnelle und langsame Achse projiziert werden. Hier ist nur die optische Achse (parallel zur langsamen Achse bei positiv doppelbrechenden Materialien) gezeichnet.
Dies Abbildung zeigt, wie ein unter dem Winkel α zur optischen Achse polarisierter Strahl auf das Plättchen fällt und das elektrische Feld auf die schnelle und langsame Achse projiziert werden. Hier ist nur die optische Achse (parallel zur langsamen Achse bei positiv doppelbrechenden Materialien) gezeichnet.Licht, welches parallel zur schnellen Achse polarisiert ist, benötigt weniger Zeit zum Durchlaufen des Mediums als Licht, welches senkrecht dazu polarisiert ist. Man kann sich das Licht in zwei Komponenten senkrecht (ordentlicher Strahl) und parallel (außerordentlicher Strahl) zur optischen Achse aufgeteilt vorstellen, die nach dem Durchlaufen des Plättchens eine Phasenverschiebung von
aufweisen. Dabei ist d die Dicke des Plättchens und λ die Wellenlänge des eingestrahlten Lichtes. Die beiden Strahlen überlagern sich hinter dem Kristall (Interferenz) zum ausgehenden Licht. Durch die (kohärente) Überlagerung dieser beiden Strahlen ergibt sich dann eine neue Polarisation des Lichtes (Frequenz und Wellenlänge bleiben erhalten; siehe nächster Abschnitt). Wie man an der Formel sieht, ist eine solche Wellenplatte also immer nur für eine bestimmte Wellenlänge ausgelegt. Es sei noch bemerkt, dass die Aufspaltung in zwei Strahlen nur eine Art Rechentrick ist. In der Realität überlagern sich diese beiden Strahlen natürlich an jeder Stelle des Kristalls. Die Elektronen um die Kristallatome bilden lokale und momentane Dipole, die in einer Überlagerung der beiden Polarisationsrichtungen der Strahlen schwingen.
λ/4-Plättchen
Wählt man d in obiger Formel so, dass sich gerade eine Phasenverschiebung um π/2 ergibt, so erhält man ein λ/4-Plättchen.
Trifft nun ein linear polarisierter Lichtstrahl, dessen Polarisationsrichtung um 45° zur optischen Achse gedreht ist, auf das Plättchen, dann entsteht zirkular polarisiertes Licht. Ist die Einstellung von 45° verschieden, so entsteht im allgemeinen Fall elliptisch polarisiertes Licht. Ursächlich hierfür ist, dass der Lichtstrahl in zwei senkrecht zueinander polarisierte Anteile aufgespalten wird, die sich am Ausgang des Plättchens um eine Viertelphase verschoben wieder überlagern. Damit entsteht für den resultierenden Feldvektor des austretenden Lichtstrahls eine Lissajous-Figur (Kreis oder Ellipse), die während jedes Schwingungszyklus eine vollständigen Drehung der Polarisationsebene um 360° hervorruft. Man nennt ein λ/4-Plättchen daher auch Zirkularpolarisator.
Ist die Polarisationsrichtung des einfallenden Lichts dagegen parallel zu einer der Achsen, dann erhält man nach dem Plättchen wieder linear polarisiertes, aber phasenverschobenes Licht.
Umgekehrt verwandelt ein λ/4-Plättchen auch zirkular polarisiertes Licht in linear polarisiertes Licht. Zwei hintereinander geschaltete λ/4-Plättchen ergeben bei paralleler Ausrichtung ihrer optischen Achse ein λ/2-Plättchen.
λ/2-Plättchen
Ergibt sich oben eine Verschiebung um π, so erhält man ein λ/2-Plättchen. Man kann ein solches Plättchen zur Drehung der Polarisationsrichtung benutzen. Wird Licht unter dem Winkel α zu einer optischen Achse eingestrahlt, so kommt das Licht unter dem Winkel -α (also um den Winkel 2α zur optischen Achse hin gedreht) wieder heraus.
Mathematische Beschreibung
Man betrachte eine linear in y-Richtung polarisierte, ebene Welle in z-Richtung
Um eine physikalisch reale Größe zu beschreiben verwendet man nur den Realteil obiger komplexer Beschreibung, also:
Der Vektor
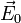 ist ein Vektor in der x-y-Ebene. Diese treffe nun senkrecht auf eine Wellenplatte, deren schnelle Achse unter dem Winkel α zur y-Richtung verkippt ist (siehe Zeichnung oben). Wir wechseln nun in das Koordinatensystem der Achsen der Wellenplatte! Dann wird
ist ein Vektor in der x-y-Ebene. Diese treffe nun senkrecht auf eine Wellenplatte, deren schnelle Achse unter dem Winkel α zur y-Richtung verkippt ist (siehe Zeichnung oben). Wir wechseln nun in das Koordinatensystem der Achsen der Wellenplatte! Dann wird 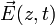 auf die Achsen projiziert und man erhält:
auf die Achsen projiziert und man erhält:Das Wellenplättchen bewirkt nun eine Phasenverzögerung
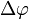 der langsamen Achse (
der langsamen Achse (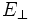 -Anteil) gegenüber der schnellen Achse, man erhält also:
-Anteil) gegenüber der schnellen Achse, man erhält also:Für ein λ/4-Plättchen gilt
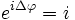 . Betrachtet man dann nur noch den Real-Teil der komplexen Schreibweise (entspricht der realen physikalischen Größe, z. B. E-Feld), so ergibt sich:
. Betrachtet man dann nur noch den Real-Teil der komplexen Schreibweise (entspricht der realen physikalischen Größe, z. B. E-Feld), so ergibt sich:Dies entspricht aber einer Bewegung des E-Feldvektors in der x-y-Ebene in Raum und Zeit. Für α=45° gilt
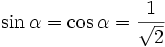 und man erhält eine Kreisbahn für die Spitze des E-Feldvektors. Für andere Winkel ergibt sich eine Ellipse.
und man erhält eine Kreisbahn für die Spitze des E-Feldvektors. Für andere Winkel ergibt sich eine Ellipse.Bei einem λ/2-Plättchen gilt
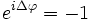 und entsprechend:
und entsprechend:Dies entspricht einer Drehung der Polarisation um den Winkel 2 α.
Siehe auch
Links
Literatur
- Wolfgang Demtröder: Experimentalphysik 2. Springer 2004
- Gerthsen; Meschede: Gerthsen Physik. Springer-Verlag 22. Auflage 2004 ISBN 3-540-02622-3
- B. E. A. Saleh, M. C. Teich: Fundamentals of Photonics. John Wiley 1991
Wikimedia Foundation.

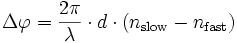


![\vec{E}(z,t)=\vec{E}_0\cdot\exp\left[i(\omega t-kz)\right]=E_0\cdot\begin{pmatrix}0\\1\end{pmatrix}\cdot\exp\left[i(\omega t-kz)\right].](/pictures/dewiki/102/f8084b8a1a3527499e6397a2f3c4a30d.png)
![\vec{E}(z,t)=\vec{E}_0\cdot\cos\left[(\omega t-kz)\right]](/pictures/dewiki/51/37090b2225a3ebea56a34fd86c12bf89.png)
![\vec{E}(z,t)=\begin{pmatrix}E_\|\\E_\bot\end{pmatrix}\cdot\exp\left[i(\omega t-kz)\right]=E_0\cdot\begin{pmatrix}\cos\alpha\\\sin\alpha\end{pmatrix}\cdot\exp\left[i(\omega t-kz)\right].](/pictures/dewiki/102/f3f7f7409ea11c97c3fcac1e82cb7bf7.png)
![\vec{E}(z,t)=E_0\cdot\begin{pmatrix}\cos\alpha\\e^{i\Delta\varphi}\cdot\sin\alpha\end{pmatrix}\cdot\exp\left[i(\omega t-kz)\right].](/pictures/dewiki/97/a03887058521f4e0417aced3f18deaa3.png)
![\vec{E}(z,t)=E_0\cdot\begin{pmatrix}\cos\alpha\cdot\cos\left[(\omega t-kz)\right]\\-\sin\alpha\cdot\sin\left[(\omega t-kz)\right]\end{pmatrix}.](/pictures/dewiki/56/8abf3b9c16640b707bb44f948778d55b.png)
![\vec{E}(z,t)=E_0\cdot\begin{pmatrix}\cos\alpha\\-\sin\alpha\end{pmatrix}\cdot\exp\left[i(\omega t-kz)\right].](/pictures/dewiki/51/361e26056270660641a82060e272f04c.png)