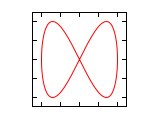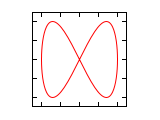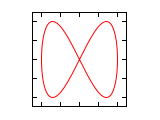- Lissajous-Figur
-
Lissajous-Figuren sind Kurvengraphen, die durch Überlagerung harmonischer Schwingungen entstehen. Sie sind benannt nach dem französischen Physiker Jules Antoine Lissajous (1822–1880). Einen besonders faszinierenden Anblick bietet die Kurve bei geringfügiger Abweichung zwischen den Schwingungen, weil durch die langsam rotierende Figur ein 3D-Eindruck entsteht. In jüngerer Zeit spielten sie zum Beispiel bei der Ausbildung zum tieferen Verständnis von Wechselströmen mit Hilfe des Oszilloskops eine Rolle.
 Diese Animation zeigt eine Lissajous-Figur, wie sie ein Oszilloskop, bei einem Frequenz-Verhältnis von annähernd (nicht genau!) 2:3 anzeigen würde (Amplituden-Verhältnis 1:1)
Diese Animation zeigt eine Lissajous-Figur, wie sie ein Oszilloskop, bei einem Frequenz-Verhältnis von annähernd (nicht genau!) 2:3 anzeigen würde (Amplituden-Verhältnis 1:1)Inhaltsverzeichnis
Mathematische Beschreibung
Mathematisch handelt es sich um parametrische Schaubilder von Funktionen der Form
Eine solche Funktion ist genau dann periodisch, wenn das Frequenzverhältnis
rational ist, sich also in einen ganzzahligen Bruch umwandeln lässt. In diesem Falle erhält man eine geschlossene Figur. Beispielsweise ergeben die Frequenzverhältnisse
dieselbe Kurve. Andernfalls ist die Kurve nicht periodisch und liegt dicht im Rechteck
![[-A_x,A_x] \times [-A_y,A_y]](0/e705dc20cd09d2738f8dfcf110aae2b3.png) .
.Anmerkung: Das Bild oben zeigt die Darstellung ähnlich einem Oszilloskop. Dort führt eine fehlende Abstimmung der beiden Schwingung nicht zu einem ausgefüllten Rechteck, da bedingt durch das zeitlich begrenzte Nachleuchten der Bildröhre immer nur ein Teil des Kurvenverlaufs abgebildet wird.
Die Amplituden Ax und Ay skalieren die Figuren lediglich horizontal beziehungsweise vertikal. Das Erscheinungsbild der Graphen hängt vor allem vom Frequenzverhältnis v und der Phase φ ab. Hat v den Wert 1, ergibt Δφ = φ1 - φ2 die Phasenverschiebung zwischen den Schwingungen. Ist v eine rationale Zahl ungleich 1, erfolgt die Angabe Δφ gewöhnlich für die minimale Phasendifferenz. Des Weiteren ist es erforderlich, für welche Schwingung die Angabe erfolgt.
Der Abschnitt Abbildungen für Frequenzverhältnis 1:n und n:1 Abbildungen für Frequenzverhältnis n1:n2 zeigen Lissajous-Figuren für verschieden Frequenzverhältnisse und Phasendifferenz, der darauf folgende Abschnitt Lissajous-Figuren im Oszilloskop und danach erläutert Methoden zur messtechnischen Ermittelung der Figuren.
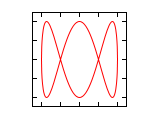
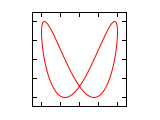
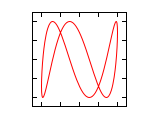
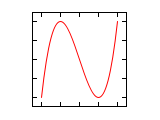
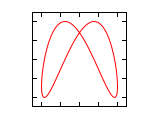
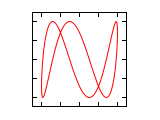
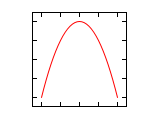
Abbildungen für Frequenzverhältnis 1:n und n:1 (Amplituden-Verhältnis 1:1)
Die Phasendifferenz Δφ bezieht sich in den folgenden Abbildungen immer auf die größere Frequenz. Ist die Frequenz auf der horizontalen Achse höher, entsteht bei nicht vollständig abgeglichener Frequenz der Eindruck einer Drehung um die senkrechte Achse und im umgekehrten Fall um die waagrechte Achse.
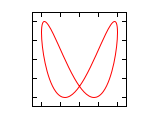
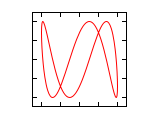
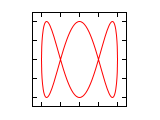
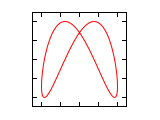
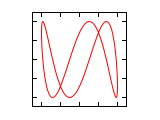
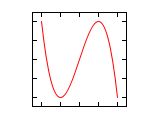
Δφ 1:1 1:2 1:3 2:1 0 ¹/₄·π ¹/₂·π ³/₄·π 1·π 1¹/₄·π 1¹/₂·π 1³/₄·π 2·π Abbildungen für Frequenzverhältnis n1:n2 (Amplituden-Verhältnis 1:1)
Für Verhältnisangaben, bei denen weder der Zähler noch Nenner den Wert 1 tragen erreicht Δφ nicht den Maximalwert 2·π, die Wiederholung des Kurvenmusters fängt bereits vorher an. Dieser Effekt entsteht, da zur Bildung der Figur eine Anzahl von n1 Schwingungen des ersten Signals und n2 Schwingungen des zweiten Signals erforderlich sind. Entsprechend gilt es mehr Nulldurchgänge für die Ermittlung der maximalen Phasendifferenz zu berücksichtigen.
Δφ 2:3 Δφ 3:4 0 
0 
¹/₂·¹/₄·π 
¹/₃·¹/₄·π 
¹/₂·¹/₂·π 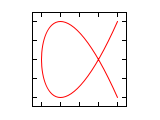
¹/₃·¹/₂·π 
¹/₂·³/₄·π 
¹/₃·³/₄·π 
¹/₂·π 
¹/₃·π 
5/8·π 
5/12·π 
³/₄·π 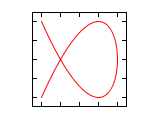
¹/₂·π 
7/8·π 
7/12·π 
1·π 
²/₃·π 
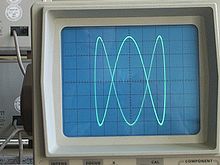
Lissajous-Figuren im Oszilloskop
Bei der Arbeit mit dem Oszilloskop erhält man Lissajous-Figuren, wenn man bei abgeschalteter Zeitablenkung sowohl an den Eingang für die y- als auch für die x-Ablenkung eine harmonische Wechselspannung anlegt.
Die Form der Figuren erlaubt genaue Rückschlüsse auf Frequenz und Phasenlage der beiden Spannungen. Bei gleichen Frequenzen (bspw: v = 1:1) kann man an der elliptischen Figur die Phasendifferenz ablesen. Bei zwei fast gleichen Frequenzen (oder einem Frequenzverhältnis, das sehr nahe an einem der einfachen rationalen Verhältnisse liegt) zeigt der Schirm des Oszilloskops eine zwar geschlossene, aber sich zeitlich verändernde Figur. So kann man mit hoher Empfindlichkeit kleine Frequenzunterschiede messen.
Deshalb waren Lissajous-Figuren beispielsweise in der Werkstatt von Fernseh- und Röhrentechnikern ein alltägliches Bild. Andererseits wirken sie in ihrer Vielfalt besonders (aber nicht nur) auf den technischen Laien äußerst faszinierend, gerade in der leicht animierten Form. Deshalb wurden in Filmkunst und Fernsehen auch häufig Monitore im Bühnenbild mit Lissajous-Figuren dekoriert, wenn eine Umgebung sehr modern oder futuristisch wirken sollte, etwa in Science-Fiction-Filmen und -Serien.
Mechanische Erzeugung von Lissajous-Figuren
 Harmonograph: zwei Platten bewegen sich rechtwinklig harmonisch zueinander (Antrieb: Kreuzschleifengetriebe[1]). Die Kreuzungsstelle zweier Schlitze bewegt sich auf einer Lissajous-Figur, die mit durchgestecktem Schreibstift registrierbar ist.[2]
Harmonograph: zwei Platten bewegen sich rechtwinklig harmonisch zueinander (Antrieb: Kreuzschleifengetriebe[1]). Die Kreuzungsstelle zweier Schlitze bewegt sich auf einer Lissajous-Figur, die mit durchgestecktem Schreibstift registrierbar ist.[2]
- Siehe hierzu auch: Harmonograph
Lissajous-Figuren lassen sich zum Beispiel mit einem mechanischen, als Harmonograph ausgebildeten Schreiber herstellen (s. Abbildung).
Eine häufig angewendete einfachere Methode ist das Zeichnen mittels eines unter einer pendelnden Masse befestigten Stiftes in eine Sandfläche, über der die Masse pendelt. Will man zwei Schwingungen mit unterschiedlicher Frequenz kombinieren, kann man zum Beispiel einen mit Sand gefüllten Teller benutzen und diesen ebenfalls pendelnd aufhängen (Aufhängeschnüre am Tellerrand, so dass die in der Mitte am gleichen Haken hängende Masse Bewegungsspiel hat). Möglich ist auch, die Spur mit aus der pendelnden Masse auslaufender Tinte oder ausrinnendem Sand zu zeichnen, wobei die Schwingungen weniger gebremst werden.
Eine Methode zum Selbstbau ist die folgende:
Man druckt eine Sinuskurve so auf eine transparente Folie, dass man eine ganzzahlige Anzahl an Perioden erhält, und Nullpunkt, Berg oder Tal an beiden Seiten der Folie identisch sind. Im Zweifelsfalle ist die Folie etwas zurecht zu schneiden. Dann klebt man die beiden Seiten der Folie zusammen, so dass man einen transparenten Zylinder erhält. Wer mehr Geschick hat, kann auch einen Glaszylinder per Hand bemalen. Durch Drehen des Zylinders bekommt man, beim seitlichen Durchsehen, die verschiedenen Ansichten der jeweiligen Lissajous-Figur. Problematisch ist dabei das Erzeugen von Lissajous-Figuren bei gebrochenen Perioden-Verhältnissen wie 2:3 oder 3:5, da sich die Sinusfunktion überlappt.Einzelnachweise
- ↑ Darstellung harmonischer Schwingungen mit Kreuzschleifengetriebe [1]
- ↑ Ein Kurvenschreiber als Harmonograph [2]
Weblinks
Wikimedia Foundation.