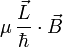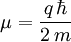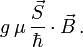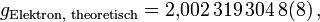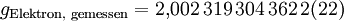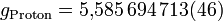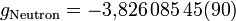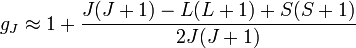Landefaktor

In der Physik gibt der Landé-Faktor (nach Alfred Landé) oder gyromagnetische Faktor für ein geladenes Teilchen im Magnetfeld an, um wie viel stärker sich der Spin auf seine Energie auswirkt als ein gleich großer Bahndrehimpuls.

Der Drehimpuls 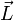$\vec{L}$ eines geladenen Punktteilchens trägt im Magnetfeld 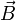$\vec{B}$ zur Energie mit

$\mu\, \frac{\vec L}{\hbar}\cdot \vec{B}$

bei. Dabei ist 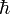$\hbar$ das Plancksche Wirkungsquantum und

$\mu = \frac{q\,\hbar}{2\,m}$

das Magneton des Teilchens mit Masse m und Ladung $q\,.$

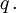
Der Betrag des Magnetons des Elektrons heißt Bohrsches Magneton. Das Magneton des Protons ist etwa zweitausend mal kleiner und heißt Kernmagneton.

Der Landé-Faktor g tritt in der entsprechenden Energie auf, mit der der Spin 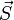$\vec{S}$ im Magnetfeld zur Energie beiträgt,

$g\,\mu\, \frac{\vec S}{\hbar}\cdot \vec{B}\,.$

Theorie und Experiment

In der theoretischen Beschreibung des Elektrons durch die Schrödinger-Gleichung gibt es zunächst keinen Spin. Man kann ihn mit der Pauli-Gleichung einbeziehen. Dabei ist der gyromagnetische Faktor in dieser nichtrelativistischen Gleichung frei wählbar, also unerklärt. Das ist in der relativistischen Beschreibung des Elektrons durch die Dirac-Gleichung für Spin-½-Fermionen anders: sie sagt den gyromagnetischen Faktor g = 2 voraus.

Erste Messungen des gyromagnetischen Faktors des Elektrons ergaben einen Wert von etwa 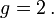$g=2\,.$ Genauere Experimente zeigten dann geringe Abweichungen des Landé-Faktors von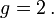 $g=2\,.$

Die Dirac-Gleichung berücksichtigt nicht die mögliche Erzeugung und Vernichtung von Photonen und Elektron-Positronpaaren. Dies leistet erst die Quantenelektrodynamik. In ihr wird die Ankopplung des Elektrons an das Magnetfeld korrigiert. Diese Korrekturen liefern für den Landé-Faktor des Elektrons einen theoretischen Wert von

$g_{\text{Elektron, theoretisch}} = 2{,}002\,319\,304\,8(8) \,,$

wohingegen das genaueste Experiment einen Wert von

$g_{\text{Elektron, gemessen}} = 2{,}002\,319\,304\,362\,2(22)$

für den Landé-Faktor des Elektrons ergibt. Dies ist die wohl genaueste Übereinstimmung von Experiment und Theorie in den Naturwissenschaften. Die Abweichung vom Wert g=2 der Diractheorie wird als anomales magnetisches Moment bezeichnet. Die präzise Berechnung des g-Faktors und der Vergleich mit dem Experiment etwa beim Myon dient zu Präzisionstests des Standardmodells der Elementarteilchen.

Zusammengesetze Teilchen haben deutlich andere gyromagnetische Faktoren.

• $g_{\text{Proton}}=5{,}585\,694\,713(46)$
• $g_{\text{Neutron}}=-3{,}826\,085\,45(90)$

Beim gyromagnetischen Faktor des Neutrons handelt es sich genau genommen um die Stärke der Spin-Magnetfeld-Energie des Neutrons im Vergleich zur Bahndrehimpuls-Magnetfeld-Energie des Protons, denn das Neutron ist ungeladen und hat keine Bahndrehimpuls-Magnetfeld-Energie.

Die gyromagnetischen Faktoren von Proton und Neutron sind in der theoretischen Physik nicht genau berechenbar, da nicht genügend genau bekannt ist, wie sich in ihnen die Bestandteile, Quarks und Gluonen, verhalten.

Bestimmung des Landé-Faktors eines Atoms

Für ein Atom errechnet sich der dem Gesamtdrehimpuls 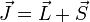$\vec{J}=\vec{L}+\vec{S}$ zugehörige Landé-Faktor näherungsweise (dh. ohne Korrekturen der Quantenelektrodynamik) nach:

$g_J \approx 1+\frac{J(J+1)-L(L+1)+S(S+1)}{2J(J+1)}$

S ist dabei die Summe der Elektronenspins, L ist die Summe der Bahndrehimpuls-Quantenzahlen und J=L+S bei mehr als halb-vollen Schalen und sonst J=L-S. Für die Berechnung werden nur die Valenzelektronen hergenommen, die sich nach den Hundschen Regeln auf die verschiedenen Niveaus der höchst besetzten Schale verteilen, da die Drehimpuls- und Spin-Quantenzahlen abgeschlossener Schalen zu Null koppeln.

Siehe auch

• Herleitung des gyromagnetischen Faktors aus der Dirac-Gleichung