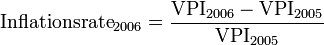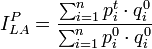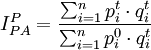Laspeyres-Preisindex

Jährliche Preisveränderungsraten in Deutschland von 1965 bis 2004

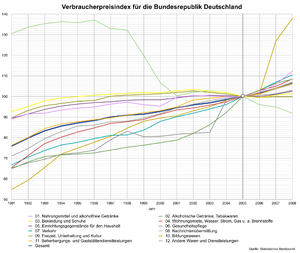Verbraucherpreisindex in Deutschland, 1991 bis 2008, Jahr 2005=100

CPIs in unterschiedlichen Länder im Verlaufe der Zeit

Ein Preisindex ist ein statistisches Konstrukt, das eine Aussage über die Höhe der Inflation, bzw. Deflation in einem volkswirtschaftlichen Bereich machen soll. Dazu wird ermittelt, wie sich die Preise der Güter eines für diesen Wirtschaftsbereich repräsentativen Warenkorbes im Durchschnitt über die Zeit geändert haben.

In der Preisstatistik wird ein ganzes Bündel von Preisindizes ermittelt. Die folgenden Betrachtungen werden der Einfachheit halber nur für einen Einkaufs-Preisindex (z. B. Verbraucherpreisindex) angestellt.

Es sind zwei Konzepte der Bildung von Preisindizes weit verbreitet:

1. Der Preisindex nach Laspeyres
2. Der Preisindex nach Paasche

In der Volkswirtschaftlichen Gesamtrechnung wird dagegen entsprechend internationalen Konventionen – in Deutschland ab 2005 – eine Preisbereinigung mit sog. Kettenindizes (chain prices) vorgenommen.

Alternative Definitionen

„Verbraucherpreisindex (VPI) […] berechnet die Kosten für eine detaillierte Liste von Gütern und Dienstleistungen in Euro (früher als Preisindex für die Lebenshaltung bezeichnet)“

– Blanchard und Illing, 2006 ^[1]

„misst die durchschnittliche Preisveränderung aller Waren und Dienstleistungen, die von privaten Haushalten für Konsumzwecke gekauft werden“

– Sieg, 2007 ^[2]

„Preisindizes sind, vereinfacht ausgedrückt, Funktionen, die die Preise und deren Veränderungen aggregieren und zu einer Messzahl zusammenfassen, die eine Aussage über die Preisentwicklung als Ganzes zulässt.“

– Hanusch und Kuhn, 1992 ^[3]

Einordnung

Ein wichtiges wirtschaftspolitisches Ziel ist seit jeher Preisniveaustabilität. Um zu überprüfen ob ein Preisniveau konstant ist, bzw. wie hoch seine Änderung ist, wird eine Inflationsrate berechnet:

$\text{Inflationsrate}_\text{2006} = \frac{\text{VPI}_\text{2006} - \text{VPI}_\text{2005}}{\text{VPI}_\text{2005}}$

mit VPI₂₀₀₅ = Verbraucherpreisindex des Jahres 2005 und VPI₂₀₀₆ = Verbraucherpreisindex des Jahres 2006.

Primär interessant ist, wie sich die Kaufkraft des Geldes der Konsumenten im Zeitverlauf ändert. Deshalb wird in der Praxis vorwiegend der Verbraucherpreisindex berechnet, da dieser nur solche Waren und Dienstleistungen erfasst, die für die privaten Haushalte bestimmt sind. Der Verbraucherpreisindex (VPI) wird monatlich vom Statistischen Bundesamt berechnet. Andere mögliche Preisindizes sind bspw. der Index der Ein- und Ausfuhrpreise, der Index der Erzeugerpreise landwirtschaftlicher oder industrieller Produkte sowie der Index des Bruttoinlandsproduktes. ^[4] Auch Aussagen über regionale Preisniveau-Unterschiede können mit einem Preisindex ausgedrückt werden, der dann in analoger Weise wie der zeitliche Preisindex aufgebaut ist. Derartige Preisindizes werden jedoch selten ermittelt.

Bei einem zeitlichen Preisindex, der im Folgenden näher betrachtet werden soll, ist es zunächst einmal notwendig zwei Zeitpunkte zu bestimmen zu denen der Preis des Warenkorbes ermittelt werden soll. Diese werden „Basisjahr“ (oder auch „Basisperiode“) und Berichtsjahr genannt. Dabei ist das Basisjahr das Jahr auf das sich die Untersuchung bezieht (der Startpunkt der Betrachtung) und das Berichtsjahr das Jahr indem der Preisindex erstellt wird (sozusagen das aktuelle Jahr, bzw. der Endpunkt der Betrachtung). Bei der Bestimmung von Veränderungen eines Preisindex wird das Basisjahr gleich 100% gesetzt. Es sollte immer so gewählt werden, dass es möglichst gut im aktuellen Trend der Entwicklung liegt.

Der Preis eines Warenkorbes ist die Summe der einzelnen Güterpreise, die er beinhaltet. Diese werden mit den jeweiligen Verbrauchsmengen der Güter multipliziert, d.h. „mit ihrem Anteil an den Gesamtausgaben des Haushaltes gewichtet.“ ^[5] Aus welchem Jahr diese Gewichtungen stammen unterscheidet den Laspeyres-Index und den Paasche-Index.

Laspeyres-Index

Bei der Berechnung des Preisindex nach Étienne Laspeyres stammen die gewählten Gewichte (d.h. die Verbrauchsmengen) aus dem Basisjahr. Der Index ermittelt den Preis eines Warenkorbes in der Zusammensetzung des Basisjahres zu Güterpreisen des Berichtsjahres bezogen auf den Preis des gleichen Warenkorbes (gleiche Verbrauchsmengen) zu Güterpreisen des Basisjahres. Dies wird in einem Quotienten ausgedrückt:

$I_{LA}^P=\frac{\sum_{i=1}^n p_i^t \cdot q_i^0}{\sum_{i=1}^n p_i^0 \cdot q_i^0}$

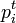mit $p_i^t$ = Preise bzgl. Berichtsjahr, 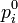$p_i^0$ = Preise bzgl. Basisjahr, 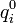$q_i^0$ = Verbrauch bzgl. Basisjahr

Es wird also untersucht was der alte Warenkorb (Verbrauchsmengen des Basisjahres) heute kosten würde (Preise des Berichtsjahres) und was für den gleichen Warenkorb im Basisjahr bezahlt werden musste (alte Preise und Mengen des Basisjahres). Es wird unterstellt, dass die Mengen und Qualitäten der Güter im Warenkorb im Zeitverlauf konstant sind, sodass sich Veränderungen des Indexes nur durch Veränderungen der Güterpreise ergeben können.

Der praktische Vorteil von Laspeyres-Indizes besteht darin, dass die Gewichte nur für das Basisjahr ermittelt werden müssen und dann unverändert bleiben. Damit sie trotzdem als repräsentativ für das aktuelle Preisgeschehen gelten können, werden sie in der amtlichen Statistik – ebenso wie die Zusammensetzung des Warenkorbes – regelmäßig (in der Regel alle 5 Jahre) aktualisiert. Jedoch bieten die konstanten Verbrauchsmengen den Vorteil, dass die einzelnen Preisindizes, die mit dem gleichen Basisjahr erstellt wurden, sehr gut vergleichbar sind.

Die Bestimmung des Verbraucherpreisindex erfolgt in Deutschland mit Hilfe eines Laspeyres-Index.

Paasche-Index

Im Unterschied zum Laspeyres-Index stammen die gewählten Gewichte bei der Berechnung des Preisindex nach Hermann Paasche aus dem aktuellen Berichtsjahr, nicht aus dem Basisjahr. Er vergleicht den Preis eines Warenkorbes in der Zusammensetzung des Berichtsjahres zu Güterpreisen des Berichtsjahres mit dem Preis des gleichen Warenkorbes (aktuelle Verbrauchsmengen des Berichtsjahres) zu Güterpreisen des Basisjahres. Dies kann ebenfalls als Quotient ausgedrückt werden:

$I_{PA}^P=\frac{\sum_{i=1}^n p_i^t \cdot q_i^t}{\sum_{i=1}^n p_i^0 \cdot q_i^t}$

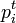mit $p_i^t$ = Preise bzgl. Berichtsjahr, 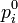$p_i^0$ = Preise bzgl. Basisjahr, 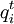$q_i^t$ = Verbrauch bzgl. Berichtsjahr

Es wird also untersucht, was ein aktueller Warenkorb (aktuelle Preise und Mengen des Berichtsjahres) kostet und was für den gleichen Warenkorb (Verbrauchsmengen des Berichtsjahres) im Basisjahr hätte bezahlt werden müssen (Preise des Basisjahres).

Ein (reiner) Paasche-Preisindex wird von der amtlichen Statistik selten berechnet, da er durch die notwendigen regelmäßigen Aktualisierungen der Verbrauchsmengen ressourcen- und zeitaufwendig ist und sich die ständig wechselnden Gewichte negativ auf die Vergleichbarkeit einzelner Jahre auswirken. Er wird aber bei der Deflationierung von Umsatzentwicklungen benötigt, um „echte“ Mengenentwicklungen als Laspeyres-Mengenindizes zu erhalten.

"Wenn man beim Paasche-Index vor einem ähnlichen Dilemma wie beim Laspeyres-Index steht - lange Zeitreihen mit hohem Informationsgehalt über die Inflationsrate, aber problematischem Mengengerüst (Laspeyres) oder exaktem Mengengerüst, aber geringem Aussagewert über die Inflationsrate (Paasche) -, ist es konsequent, den weniger aufwendigen Laspeyres-Index zu wählen." ^[6]

Weitere Indizes

Neben Paasche und Laspeyres existieren noch weitere Indizes, die wegen ihrer geringeren praktischen Relevanz hier nur kurz aufgeführt werden.

Fisher-Preisindex

Der Fisher-Preisindex (benannt nach Irving Fisher) ist das geometrische Mittel der Preisindizes nach Paasche und Laspeyres. Der Fisher-Preisindex wird in der Statistik auch „Fishers idealer Preisindex“ genannt.

Kettenpreisindex

Kettenpreisindizes (chain prices) ermitteln für jedes Jahr, wie viel die im Vorjahr gekauften Waren im aktuellen Jahr kosten (in der Laspeyresform) bzw. wie viel die im aktuellen Jahr gekauften Waren im Vorjahr gekostet haben (in der Paascheform). Dadurch wird für jedes Jahr ein anderer Warenkorb zu Grunde gelegt und so bei der Ermittlung der Preisänderungen die jeweils aktuellen Verbrauchsgewohnheiten berücksichtigt.
Nachteil des Verfahrens ist, dass die Ergebnisse von Jahr zu Jahr nicht direkt vergleichbar sind - wegen des sich wandelnden Warenkorbes - und dass längerfristige Betrachtungen nur durch Verkettung (daher der Name des Index) der Jahresergebnisse möglich sind.

Der Harmonisierte Verbraucherpreisindex wird als Kettenindex (Laspeyresform) berechnet. Er wird innerhalb der EU von allen Mitgliedsstaaten unter Zugrundelegung eines EU-weit einheitlichen Warenkorbes erhoben, was eine länderübergreifende Vergleichbarkeit der Preisentwicklung ermöglicht.

Beispiele

Warenkörbe:

	1995 (Basisjahr, 0)		2000 (Berichtsjahr, t)
	Preis	Verbrauch	Preis	Verbrauch
Zigaretten	4,-	10	5,-	7
Pizza	5,-	4	6,-	3
Kino	8,-	2	12,-	1
Bier	0,60	10	1,-	8

(Preise in GE, Verbräuche in ME)

Der repräsentative Warenkorb soll hier beispielhaft aus nur 4 Gütern bestehen, d.h. es werden typischerweise nur diese 4 Güter in den angegebenen Mengen zu den angegebenen Preisen von den Konsumenten gekauft. Wie aus der Tabelle ersichtlich mussten die Verbrauchsmengen des Warenkorbes, um weiterhin repräsentativ zu sein, von 1995 zu 2000 angepasst werden, was auf veränderte Konsumgewohnheiten zurückzuführen ist.

Laspeyres-Index

$I_{LA}^P=\frac{\sum_{i=1}^n p_i^t \cdot q_i^0}{\sum_{i=1}^n p_i^0 \cdot q_i^0}=\frac{{\color{Red}5}\cdot{\color{Blue}10}+{\color{Red}6}\cdot{\color{Blue}4}+{\color{Red}12}\cdot{\color{Blue}2}+{\color{Red}1}\cdot{\color{Blue}10}}{{\color{Red}4}\cdot{\color{Blue}10}+{\color{Red}5}\cdot{\color{Blue}4}+{\color{Red}8}\cdot{\color{Blue}2}+{\color{Red}0,60}\cdot{\color{Blue}10}}=\frac{108}{82}=1,317$

Ergebnis: Da das Basisjahr 1995 100% entspricht handelt es sich hier um einen Preisanstieg auf 131,7% (d.h. um 31,7%) im Jahr 2000 bezogen auf 1995. Der Warenkorb des Jahres 2000 verhält sich also zum Warenkorb von 1995 wie 1,317 zu 1.

Paasche-Index

$I_{PA}^P=\frac{\sum_{i=1}^n p_i^t \cdot q_i^t}{\sum_{i=1}^n p_i^0 \cdot q_i^t}=\frac{{\color{Red}5}\cdot{\color{Blue}7}+{\color{Red}6}\cdot{\color{Blue}3}+{\color{Red}12}\cdot{\color{Blue}1}+{\color{Red}1}\cdot{\color{Blue}8}}{{\color{Red}4}\cdot{\color{Blue}7}+{\color{Red}5}\cdot{\color{Blue}3}+{\color{Red}8}\cdot{\color{Blue}1}+{\color{Red}0,60}\cdot{\color{Blue}8}}=\frac{73}{55,8}=1,308$

Ergebnis: Da das Basisjahr 1995 100% entspricht handelt es sich hier um einen Preisanstieg auf 130,8% (d.h. um 30,8%) im Jahr 2000 bezogen auf 1995. Der Warenkorb des Jahres 2000 verhält sich also zum Warenkorb von 1995 wie 1,308 zu 1.

Es ergibt sich eine Abweichung zwischen beiden Berechnungsarten von 0,9%.

Bewertung

Der Preisindex kann exakt nur für Artikel angegeben werden, deren „Qualität“, d. h. deren preisbestimmende Eigenschaften unverändert bleiben. Verändern sich diese Eigenschaften, muss deren geschätzter Preiseinfluss herausgerechnet werden, um Gleiches mit Gleichem preislich gegenüber stellen zu können. Da sich bei manchen Gütern die Qualität rasch wandelt und der Preisindex in diesem Fall sehr stark von (subjektiven) Schätzungen abhängt, gehen die statistischen Ämter zunehmend dazu über, hedonische Preise zu erheben. Es existieren aber noch weitere international anerkannte und empfohlene Qualitätsbereinigungsverfahren (z.B. Ausstattungsbereinigung), mit deren Hilfe Qualitätsveränderungen herausgerechnet werden können. In der Regel empfehlen sich bestimmte Verfahren für spezielle Gütergruppen besonders, d. h. kein Qualitätsbereinigungsverfahren ist pauschal für alle Güter gleichermaßen geeignet.

Die Aussagekraft eines Preisindex wird durch diverse Probleme, die mit seiner Ermittlung verbunden sind, relativiert:

• es wird nicht nach einzelnen sozialen Gruppen der Bevölkerung, die unterschiedlich stark von Preisniveauveränderungen betroffen sein können, differenziert
• die Bildung unterschiedlicher Indexhaushalte erhöht zwar die Genauigkeit, aber auch diese Indizes stellen lediglich verfeinerte Durchschnittswerte dar, die nicht den tatsächlichen individuellen Verbrauchsgewohnheiten einzelner Haushalte entsprechen müssen
• die tatsächliche Verbrauchsstruktur kann sich im Zeitverlauf ändern, während die Zusammensetzung des verwendeten Warenkorbes bis zur Festsetzung eines neuen Basisjahres aus Gründen der Vergleichbarkeit unverändert bleibt (bei Laspeyres)
• keine Berücksichtigung von Preiselastizitäten
• ständige strukturelle Veränderungen des Güterangebots

Aufgrund dieser Faktoren, die den Preisindex beeinflussen und zu Ungenauigkeiten führen, ist es erforderlich einen Toleranzbereich zu definieren innerhalb dessen noch Geldwertstabilität herrscht. In Deutschland wird dieser von der Bundesbank mit ein bis zwei Prozent veranschlagt, d.h. schwankt ein Preisindex weniger wird er als konstant angesehen. ^[7]

Internationaler Vergleich

	Index
Europäische Union	Europäischer Verbraucherpreisindex (EVPI)
Eurozone	Verbraucherpreisindex der Eurozone (VPI-EWU)
Europäischer Wirtschaftsraum	Verbraucherpreisindex für den Europäischen Wirtschaftsraum (VPI-EWR)
USA	Personal consumption expenditures price index (PCE)
Großbritannien	Harmonisierter Konsumenten-Preisindex der EU (HICP)
Schweiz	Landesindex der Konsumentenpreise (LIK)

"Der VPI-EWU wird unter anderem von der Europäischen Zentralbank (EZB) als ein Hauptindikator für die Durchführung ihrer Geldpolitik in der Eurozone verwendet." ^[8] Die US-Notenbank (Federal Reserve System) nutzt zur Messung der Inflation den Personal consumption expenditures price index. Seit 2008 berechnet das schweizerische Bundesamt für Statistik (BFS) neben dem Landesindex der Konsumentenpreise ebenfalls den harmonisierten Verbraucherpreisindex der EU.

Einzelnachweise

1. ↑ Blanchard, Olivier und Illing, Gerhard: Makroökonomie. 4. Auflage, 2006
2. ↑ Sieg, Gernot: Volkswirtschaftslehre. 2007
3. ↑ Hanusch, Horst und Kuhn, Thomas: Einführung in die Volkswirtschaftslehre. 2. Auflage, Berlin; Heidelberg; New York; Tokyo, 1992
4. ↑ Vergleiche Hewel, Brigitte und Neubäumer, Renate: Volkswirtschaftslehre. Wiesbaden, 1994, Seite 482
5. ↑ Hewel, Brigitte und Neubäumer, Renate: Volkswirtschaftslehre. Wiesbaden, 1994
6. ↑ Woll, Artur: Allgemeine Volkswirtschaftslehre. München, 1990, Seite 492
7. ↑ Vergleiche Hewel, Brigitte und Neubäumer, Renate: Volkswirtschaftslehre. Wiesbaden, 1994, Seite 484
8. ↑ EU-Info.Deutschland

Literatur

• Peter Balastèr: Konsumentenpreisindizes: Theorie und praktische Berechnung. Haupt, Bern 1990, ISBN 3-258-04288-8
• Peter Hein van Mullingen: Quality aspects in price indices and international comparisons - applications of the hedonic method. Statistics Netherlands, Voorburg 2003, ISBN 90-357-2698-7
• Klaus Lange: Eine Theorie der Preisstatistik: Preis, Preisrelation, Preisindex. Vandenhoeck & Ruprecht, Göttingen 1979, ISBN 3-525-11279-3
• Irving Fisher, William J. Barber (Hrsg.): The making of index numbers. Pickering & Chatto, London 1997, ISBN 1-85196-232-8
• Wolfgang Eichhorn, Joachim Voeller: Theory of the price index: Fisher's test approach and generalizations. Springer, Berlin 1976, ISBN 3-540-08059-7
• Peter von der Lippe: Chain indices - a study in price index theory. Metzler-Poeschel, Stuttgart 2001, ISBN 3-8246-0638-0
• Bernd Schmidt: Der Preisindex für die Lebenshaltung aller privaten Haushalte in Gestalt eines Kettenindex. Metzler-Poeschel, Stuttgart 1997, ISBN 3-8246-0528-7

Weblinks

• Indexrechner ausprobieren und Preisstatistik verstehen – Statistisches Bundesamt Deutschland
• Preisindizes des Statistischen Bundesamtes Deutschland
• Verbraucherpreisindex Österreich
• Landesindex der Konsumentenpreise (Schweiz)
• Handbuch des International Monetary Fund (IMF) für die Methodik eines Erzeugerpreisindex (englisch)
• Handbuch der International Labour Organisation (ILO) für die Methodik eines Verbraucherpreisindex (englisch)
• Preisindex für Lebenshaltung – Deutschland – seit 1881
• Consumer Price Index (CPI)